问题引入
描述
给定一棵树,为每个顶点染成红色或蓝色。
要求:每个红点周围有且仅有一个红点,每个蓝点周围有且仅有一个蓝点。
“周围”的定义:某点周围的点指通过邻边直接连接的点。
所谓树,即没有自环、重边和回路的无向连通图。
输入描述:
第一行一个正整数 n,代表树的顶点个数.。
接下来的 n-1 行,每行两个正整数 u 和 v,代表点 u 和点 v 有一条边连接。
保证输入的一定是一棵合法的树。
输出描述:
如果可以达成染色的要求,请输出一个长度为 n 的字符串,第 i个字符代表第 i个顶点的染色情况,‘B’ 代表蓝色,‘R’ 代表红色。(若有多种合法染色的方法,输出任意一种即可)
否则直接输出-1。
求解思路
典型的树的遍历问题,树形DP的思想是,在一次树的遍历过程中,完成对应问题的求解,(填充对应的DP数组),由于树的问题的求解总是依赖于子结构的求解,往往的求解思路是:
通过DFS等遍历方式,在后序遍历的过程中完成对应问题的求解。
本题的要求是,对于当前节点,其颜色与有且仅有一个相邻节点相同。那么可以有以下的推论:
- 叶子节点只有一个相邻节点,因此叶子节点与其父亲节点颜色相同
- 父亲节点已经与叶子节点颜色相同,因此父亲节点的父亲节点颜色必然不同
实现过程
采取后序遍历的实现方式,dp[i]=0 初始化为i节点未染色,后序遍历过程,如果cur节点与其一个子节点next都是 dp[idx]=0 都是未染色,那么当前两个节点可以染成相同的颜色,(采取将dp[]=cur)标记位cur表示两者相同的颜色)
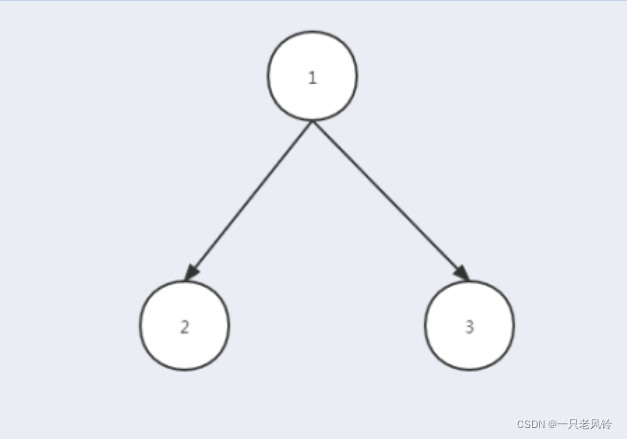
以一颗最简单的三个节点的树为例,一开始由于初始化dp[]={0}
-
因此首先遍历过程中,遇到的两个父子并且未染色的是节点1、节点2 两者可以染色为同色,dp[1]=dp[2]=1
-
当遍历到节点1和节点3时,由于节点1已经染色(被抢占)因此节点3无法寻找到配对,说明整个方案不可行
当完成dp[]数组的填充后,下一步是进行实际的填色过程,由于只有两种颜色,因此只需要遍历过程中记录当前的dp[]与parent是否相同即可:
- 若相同,那么color[cur]=color[pre]
- 若不同,那么color[cur]=!color[pre]
代码实现
#include<iostream>
#include<vector>
using namespace std;
vector<int> mp[100001]; //mp[u]表示从u节点的 相连节点集合
int color[100001];//颜色矩阵
int dp[100001]={0}; //dp[i]!=0 表示这个位置需要上一个色 (一般是 [parent,son] 一组)
void dfs1(int pre,int index)
{
//研究从index开始 其所在子树的上色问题
for(int i=0;i<mp[index].size();i++)
{
int next=mp[index][i];//孩子节点
if(next==pre)
continue; //跳过环路
dfs1(index,next); //已完成子问题求解 因为填色问题可以从叶子节点开始确定
if(!dp[index] && !dp[next]) //
{
dp[index]=index;
dp[next]=index; //全部调整为index数值
}
}
}
//开始调整颜色
void dfs2(int pre,int index)
{
for(int i=0;i<mp[index].size();i++)
{
int next=mp[index][i];
if(next==pre)
{
continue;
}
if(dp[next]==dp[index]) //下一个节点和当前节点同一颜色
color[next]=color[index];
else
color[next]=!color[index];
dfs2(index,next);//进入下一入口
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n-1;i++)
{
int u,v;
cin>>u>>v;
mp[u].push_back(v);
mp[v].push_back(u);
}
//
dfs1(-1, 1);
for(int i=1;i<=n;i++)
{
if(dp[i]<=0) //存在无法染色的节点
{
cout<<-1<<endl;
return 0;
}
}
color[1]=1;
dfs2(-1,1);
for(int i=1;i<=n;i++)
{
if(color[i]==1)
cout<<"R";
else
cout<<"B";
}
}