[数据结构与算法]最小支撑树（下）

最小支撑树（下） – 潘登同学的图论笔记

破圈法（Ⅰ）

输入： 赋权简单图$G$

输出： $G$的最小支撑树 $T=(V_T,E_T)$

算法思路：每一步都删除权值最大而且不必要的边（出现在回路中的边），直到边数=顶点数-1

• 1.把图G的边权值按不增的顺序排列成一个序列$e_1,e_2,\dots ,e_m$,$E^{\prime }\leftarrow E,E_T\leftarrow E$
• 2.若$|E_T|=|V|?1$，则输出$T=(V,E_T)$
• 3.1.否则，假设e是$E^{\prime }$中权值最大的边， E ′ ← E ′ ? { e } E'\leftarrow E'-\{e\} E′←E′?{e}
• 3.2.如果$e与E_T$中的边构成回路，则 E T ← E T ? { e } E_T\leftarrow E_T-\{e\} ET?←ET??{e},返回2

很显然，这不就是把Kruskal算法倒过来了嘛，Kruskal算法是在一个图中从下到大找构不成回路的边，但是这个就是从大到小找破坏回路的边；

算法实现

#%% 破圈法（I）
from Vertex import Vertex
from Graph import Graph
import sys
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.color = 'white'  # 新增类属性(用于记录节点是否被走过)
        self.dist = sys.maxsize  # 新增类属性(用于记录strat到这个顶点的距离)初始化为无穷大
        self.pred = None  # 顶点的前驱 BFS需要

    # 新增类方法, 设置节点颜色
    def setColor(self, color):
        self.color = color

    # 新增类方法, 查看节点颜色
    def getColor(self):
        return self.color

    # 新增类方法, 设置节点前驱
    def setPred(self, p):
        self.pred = p

    # 新增类方法, 查看节点前驱
    def getPred(self):  # 这个前驱节点主要用于追溯，是记录离起始节点最短路径上
        return self.pred    # 该节点的前一个节点是谁

    # 新增类方法, 设置节点距离
    def setDistance(self, d):
        self.dist = d

    # 新增类方法, 查看节点距离
    def getDistance(self):
        return self.dist

    def getConnections_number(self):  # 查看相邻顶点的个数，用于后面找出最小支撑树
        return len(self.connectedTo)

    def del_Connection(self, nbr):
        '''
        Parameters
        ----------
        nbr : Vertex object
            DESCRIPTION.

        '''
        self.connectedTo.pop(nbr)

class New_Graph(Graph):  # 继承Graph对象
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        if key in self.vertList:
            return
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

    def del_edge(self, start, end):
        '''  
        Parameters
        ----------
        start : Vertex object
            DESCRIPTION.
        end : Vertex object
            DESCRIPTION.

        Returns
        -------
        None.
        '''
        # 调用顶点的方法进行删除
        start.del_Connection(end)

class Queue:
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []

    def enqueue(self, items):   # 往队列加入数据
        self.items.insert(0, items)

    def dequeue(self):
        return self.items.pop()

    def size(self):
        return len(self.items)

class Stack():  # 这个栈是后进先出  将列表的尾部设置为栈顶
    def __init__(self):
        self.stack = []

    def push(self, item):
        self.stack.append(item)

    def pop(self):
        return self.stack.pop()

    def peek(self):
        if self.isEmpty():
            return None
        else:
            return self.stack[-1]

    def isEmpty(self):
        return self.stack == []

    def size(self):
        return len(self.stack)

    def __len__(self):
        return self.size()

    def __iter__(self):
        return iter(self.stack)

class Solution_1:
     def createGraph(self, g_dict=None, g_matrix=None):
        '''
        input: g_dict(邻接表) or g_matrix(邻接矩阵)
        output: directgraph(有向图)
        '''
        graph = New_Graph()
        if g_dict:
            for from_key in g_dict:
                for to_key in g_dict[from_key]:
                    # 这里就是注意提到的f跟着c走所以原图的c是[f,c],这个很重要
                    graph.addEdge(from_key, to_key[0], to_key[1])

        elif g_matrix.any():
            # 先给顶点起个名字
            name = [str(i) for i in range(1, len(g_matrix)+1)]
            for i, from_key in enumerate(name):
                for j, to_key in enumerate(name):
                    if i != j and g_matrix[i][j] != float('inf'):
                        graph.addEdge(from_key, to_key, g_matrix[i][j])
        return graph

     def Reverse_delete(self, graph):
         V = []
         E = []
         Vt = New_Graph()
         for i in graph:
             for j in graph:
                 if i != j and j in i.getConnections():
                     # 因为如果用deepcopy会有问题，我也不知道为啥不行，所以自己从够一个图
                     Vt.addEdge(i.getId(), j.getId(), i.getWeight(j))
                     V.append([i, j])
                     E.append(i.getWeight(j))
         edge_number = len(E)
         del_dege_number = 0
         while del_dege_number != edge_number - len(graph) + 1:
             e = 0
             v = None
             # 找出最大的边
             for i,k in enumerate(E):
                 if k > e:
                     v = V[i]
                     e = k
             E.remove(e)
             V.remove(v)
             # 先删除
             Vt.del_edge(Vt.getVertex(v[0].getId()), Vt.getVertex(v[1].getId()))
             # 如果删后仍然可达，就确认删除
             if self.arrive(Vt, Vt.getVertex(v[0].getId()), Vt.getVertex(v[1].getId())):
                 del_dege_number += 1
             else:  # 否则就加回
                 Vt.addEdge(v[0], v[1], e)

         Tree_v = Stack()
         for i in Vt:
             if i.getConnections_number() == 0:
                 Tree_v.push(i)
                 break
         while len(Tree_v) != 2*len(Vt)-1:
             end = Tree_v.peek()
             for i in Vt:
                 if end in i.getConnections():
                     cost = i.getWeight(end)
                     Tree_v.push(cost)
                     Tree_v.push(i)
             

         print('最小生成树是：','总长度:', sum([i for i in Tree_v if isinstance (i,float)]))
         while len(Tree_v) != 1:
             print(f'{Tree_v.pop().getId()}--', f'{Tree_v.pop()}->', end='')
         print(f'{Tree_v.pop().getId()}')
         return Vt

     def arrive(self, Vt, start, end):
         '''

         Parameters
         ----------
         Vt : New_Graph对象
             DESCRIPTION.
         start : Vertex对象
             起始顶点.
         end : Vertex对象
             终止节点.

         Returns
         -------
          : bool
             True or False.
         '''
         for i in Vt:
             i.setColor('white')
         start.setPred(None)  # 前驱节点
         vertQueue = Queue()   # 队列
         vertQueue.enqueue(start)  # 把起始节点加入图中
         while vertQueue.size() > 0:   # 当搜索完所有节点时，队列会变成空的
             currentVert = vertQueue.dequeue()  # 取队首作为当前顶点
             for nbr in currentVert.getConnections():  # 遍历临接顶点
                 if (nbr.getColor() == 'white'):   # 当邻接顶点是白色的时候
                     nbr.setColor('gray')
                     nbr.setPred(currentVert)
                     vertQueue.enqueue(nbr)
             currentVert.setColor('balck')
         return not (end.getColor()=='white')


     def draw(self, graph, Vt):
         '''
         Parameters
         ----------
         graph : graph
             原图对象.
         Vt : graph
             Kruskal算法得出的.
         Returns
         -------
         plt.
         
         '''
         plt.rcParams['font.sans-serif'] = ['SimHei']
         plt.rcParams['axes.unicode_minus'] = False
         G = nx.DiGraph()
         GT = nx.DiGraph()
         for i in graph:
             for j in graph:
                 if i != j and j in i.getConnections():
                     G.add_edge(i.getId(), j.getId(), weight=i.getWeight(j))
         for i in Vt:
             for j in Vt:
                 if i != j and j in i.getConnections():
                     GT.add_edge(i.getId(), j.getId(), weight=i.getWeight(j))
         pos = nx.spring_layout(G,seed=41)
         options = {
            "font_size": 20,
            "node_size": 200,
            "node_color": "green",
            "edgecolors": "white",
            "edge_color": 'blue',
            "font_color": 'red',
            "linewidths": 2,
            "width": 2,
            'alpha':0.8,
            'with_labels':True
            }
         plt.figure(figsize=(12,6))
         plt.subplot(121)
         nx.draw(G, pos, **options)
         plt.title('原图')
         plt.subplot(122)
         nx.draw(GT, pos, **options)
         plt.title('最小支撑树')
         plt.show()


if __name__ == '__main__':
    inf = float('inf')
    a = np.array([[0, 1, 12, inf, inf, inf],
                  [inf, 0, 9, 3, inf, inf],
                  [inf, inf, 0, inf, 5, inf],
                  [inf, inf, 4, 0, 13, 15],
                  [inf, inf, inf, inf, 0, 4],
                  [inf, inf, inf, inf, inf, 0]])
    s = Solution_1()
    graph = s.createGraph(g_matrix=a)
    Vt = s.Reverse_delete(graph)
    s.draw(graph, Vt)

• 结果如下：

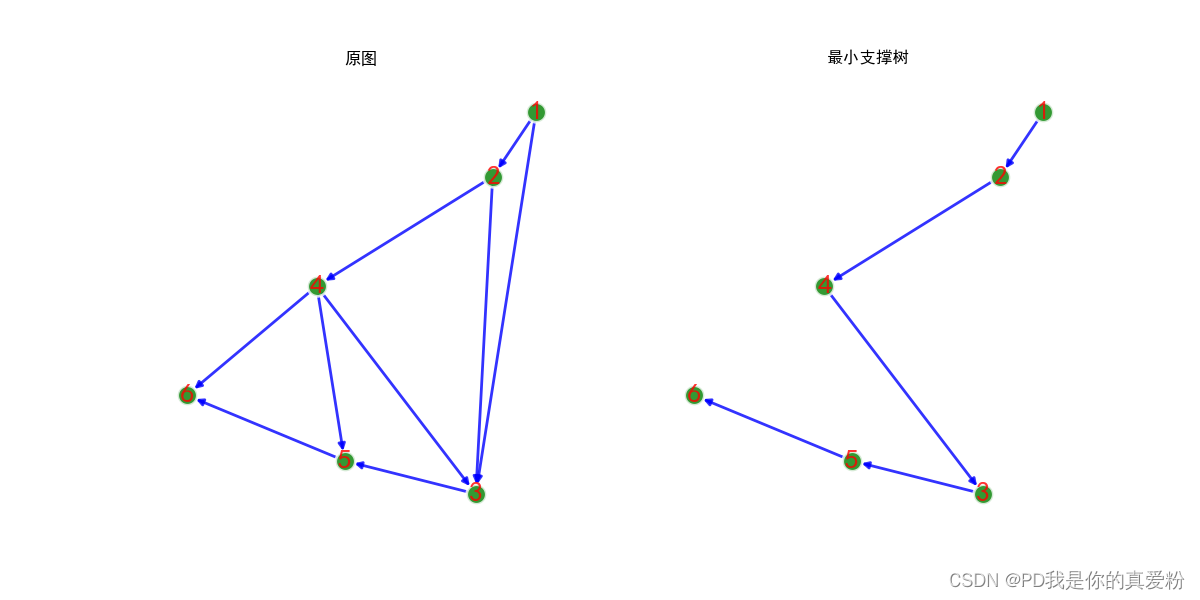
破圈法(Ⅱ)

输入： 赋权简单图$G$

输出： $G$的最小支撑树 $T=(V_T,E_T)$

因为上面的算法需要破除回路，就需要判断两点之间的可达关系，用上了BFS还是很麻烦的，而这个算法与上面的等价，但是相对简单一点

• 1.把图G的边权值按不增的顺序排列成一个序列$e_1,e_2,\dots ,e_m$,$E^{\prime }\leftarrow E,E_T\leftarrow E$
• 2.若$|E_T|=|V|?1$，则输出$T=(V,E_T)$
• 3.1.否则，假设e是$E^{\prime }$中权值最大的边， E ′ ← E ′ ? { e } E'\leftarrow E'-\{e\} E′←E′?{e}
• 3.2.如果$e不是E_T$中的桥，则 E T ← E T ? { e } E_T\leftarrow E_T-\{e\} ET?←ET??{e},返回2

算法实现

#%% 破圈法（II）
from Graph import Graph
from Vertex import Vertex
import copy
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

class New_Vertex(Vertex):  # 某一个具体问题的数据结构需要继承原有数据结构
    def __init__(self, key):
        super().__init__(key)
        self.in_degree = 0  # 新增入度属性
        self.out_degree = 0 # 新增出度属性
    
    def addNeighbor(self, nbr, weight=0):   # 重载加入节点方法
        '''
        input:
            nbr: Vertex object
            weight: int
        return:
            None
        '''
        self.connectedTo[nbr] = weight
        self.out_degree += 1
        nbr.in_degree += 1

    def get_degree(self):  # 查看度数
        return self.in_degree + self.out_degree

    def del_Connection(self, nbr):
        '''
        Parameters
        ----------
        nbr : Vertex object
            DESCRIPTION.

        '''
        self.connectedTo.pop(nbr)

class New_Graph(Graph):  # 继承Graph对象
    def __init__(self):
        super().__init__()

    # 重载方法  因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
    def addVertex(self, key):   # 增加节点
        '''
        input: Vertex key (str)
        return: Vertex object
        '''
        if key in self.vertList:
            return
        self.numVertices = self.numVertices + 1
        newVertex = New_Vertex(key)   # 创建新节点
        self.vertList[key] = newVertex
        return newVertex

    def judge_brige(self, from_Ver, to_Ver):
        # 只有两个节点的度数都不是1，才不是桥
        return (from_Ver.get_degree == 1 or to_Ver.get_degree == 1)

    def del_edge(self, start, end):
        '''  
        Parameters
        ----------
        start : Vertex object
            DESCRIPTION.
        end : Vertex object
            DESCRIPTION.

        Returns
        -------
        None.
        '''
        # 调用顶点的方法进行删除
        start.del_Connection(end)
        
class Stack():  # 这个栈是后进先出  将列表的尾部设置为栈顶
    def __init__(self):
        self.stack = []

    def push(self, item):
        self.stack.append(item)

    def pop(self):
        return self.stack.pop()

    def peek(self):
        if self.isEmpty():
            return None
        else:
            return self.stack[-1]

    def isEmpty(self):
        return self.stack == []

    def size(self):
        return len(self.stack)

    def __len__(self):
        return self.size()

    def __iter__(self):
        return iter(self.stack)

        
class Solution_2:
     def createGraph(self, g_dict=None, g_matrix=None):
        '''
        input: g_dict(邻接表) or g_matrix(邻接矩阵)
        output: directgraph(有向图)
        '''
        graph = New_Graph()
        if g_dict:
            for from_key in g_dict:
                for to_key in g_dict[from_key]:
                    # 这里就是注意提到的f跟着c走所以原图的c是[f,c],这个很重要
                    graph.addEdge(from_key, to_key[0], to_key[1])

        elif g_matrix.any():
            # 先给顶点起个名字
            name = [str(i) for i in range(1, len(g_matrix)+1)]
            for i, from_key in enumerate(name):
                for j, to_key in enumerate(name):
                    if i != j and g_matrix[i][j] != float('inf'):
                        graph.addEdge(from_key, to_key, g_matrix[i][j])
        return graph

     def Reverse_delete_plus(self, graph):
         V = []
         E = []
         Vt = copy.deepcopy(graph)
         for i in graph:
             for j in graph:
                 if i != j and j in i.getConnections():
                     V.append([i, j])
                     E.append(i.getWeight(j))
         edge_number = len(E)
         del_dege_number = 0
         while del_dege_number != edge_number - len(graph) + 1:
             e = 0
             v = None
             # 找出最大的边
             for i,k in enumerate(E):
                 if k > e:
                     v = V[i]
                     e = k
             E.remove(e)
             V.remove(v)
             if not Vt.judge_brige(Vt.getVertex(v[0].getId()), Vt.getVertex(v[1].getId())):
                 Vt.del_edge(Vt.getVertex(v[0].getId()), Vt.getVertex(v[1].getId()))
                 del_dege_number += 1

         Tree_v = Stack()
         for i in Vt:
             if i.out_degree == 0:
                 Tree_v.push(i)
                 break
         while len(Tree_v) != 2*len(Vt)-1:
             end = Tree_v.peek()
             for i in Vt:
                 if end in i.getConnections():
                     cost = i.getWeight(end)
                     Tree_v.push(cost)
                     Tree_v.push(i)
             

         print('最小生成树是：','总长度:', sum([i for i in Tree_v if isinstance (i,float)]))
         while len(Tree_v) != 1:
             print(f'{Tree_v.pop().getId()}--', f'{Tree_v.pop()}->', end='')
         print(f'{Tree_v.pop().getId()}')
         return Vt

     def draw(self, graph, Vt):
         '''
         Parameters
         ----------
         graph : graph
             原图对象.
         Vt : graph
             Kruskal算法得出的.
         Returns
         -------
         plt.
         
         '''
         plt.rcParams['font.sans-serif'] = ['SimHei']
         plt.rcParams['axes.unicode_minus'] = False
         G = nx.DiGraph()
         GT = nx.DiGraph()
         for i in graph:
             for j in graph:
                 if i != j and j in i.getConnections():
                     G.add_edge(i.getId(), j.getId(), weight=i.getWeight(j))
         for i in Vt:
             for j in Vt:
                 if i != j and j in i.getConnections():
                     GT.add_edge(i.getId(), j.getId(), weight=i.getWeight(j))
         pos = nx.spring_layout(G,seed=41)
         options = {
            "font_size": 20,
            "node_size": 200,
            "node_color": "green",
            "edgecolors": "white",
            "edge_color": 'blue',
            "font_color": 'red',
            "linewidths": 2,
            "width": 2,
            'alpha':0.8,
            'with_labels':True
            }
         plt.figure(figsize=(12,6))
         plt.subplot(121)
         nx.draw(G, pos, **options)
         plt.title('原图')
         plt.subplot(122)
         nx.draw(GT, pos, **options)
         plt.title('最小支撑树')
         plt.show()


if __name__ == '__main__':
    inf = float('inf')
    a = np.array([[0, 1, 12, inf, inf, inf],
                  [inf, 0, 9, 3, inf, inf],
                  [inf, inf, 0, inf, 5, inf],
                  [inf, inf, 4, 0, 13, 15],
                  [inf, inf, inf, inf, 0, 4],
                  [inf, inf, inf, inf, inf, 0]])
    s = Solution_2()
    graph = s.createGraph(g_matrix=a)
    Vt = s.Reverse_delete_plus(graph)
    s.draw(graph, Vt)

• 结果如下:

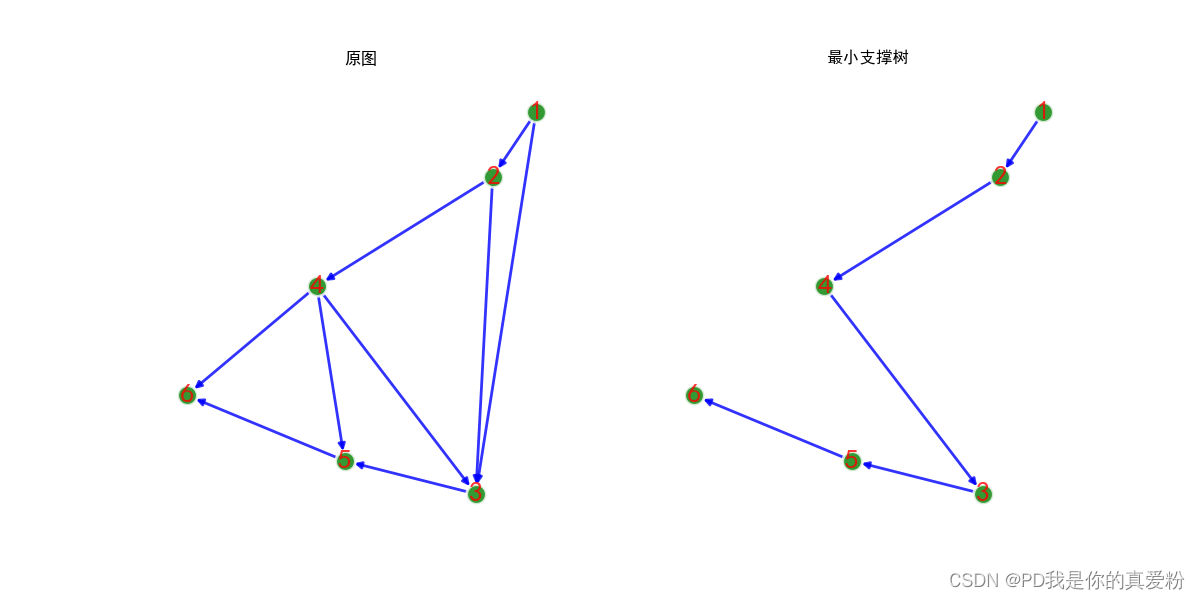
博鲁夫卡算法

输入： 赋权简单图$G$

输出： $G$的最小支撑树 $T=(V_T,E_T)$

算法思路：每一步都选择最相近的两个连通分支合并，直到剩下最后一个连通分支

• 1.$E_T\leftarrow ?$, 图G中的每个顶点v都作为一个连通分支，$C\leftarrow (V,E_T)$
• 2.对图C中的每两个不同的连通分支，选择权重最小的边$e=uv$, E T ← E T ∪ { e } , C ← ( V , E T ) E_T\leftarrow E_T \cup \{e\},C\leftarrow (V,E_T) ET?←ET?∪{e},C←(V,ET?)
• 3.若只有一个连通分支，则输出$T=(V,E_T)$,否则返回步骤2

注意 这里出现了连通分支，之前在图的分类那里说过，连通分支的特点就是互相可达，所以这就要求图是无向图，因为一个连通的有向图，就算把原图原封不动的输出，也可能不是一个连通分支；

如下图，这个就是三个连通分支

算法实现

#%%  博鲁夫卡算法

import numpy as np
import copy
import networkx as nx
import matplotlib.pyplot as plt

class Solution(object):
    def min_merge(self, a, i, j, index=None):
        '''
        用于合并两行（列），并且以两行（列）的小的值作为新一行（列）的值
    
        Parameters
        ----------
        a : array

        i : int
            第一行（列）.
        j : int
            第二行（列）.
        Returns
        -------
        result
            处理后的array.
        index
            修改的index
        '''
        result = copy.deepcopy(a)
        ai = result[i, :]
        aj = result[j, :]
        temp = []
        if not isinstance(index, np.ndarray):
            index = [[(0,0)]*len(result) for _ in range(len(result))]
            index = np.array(index)
            for a in range(len(result)):
                for b in range(len(result)):
                        index[a, b] = (a, b)
        for s,b in zip(ai,aj):
            bool_index = ai>aj
            for k in range(len(bool_index)):
                if k:
                    index[i, k] = index[j, k]
            temp.append(min(s,b))
        for k in range(len(temp)):
            result[i,k] = temp[k]
        result = np.delete(result,j,axis=0)
        index = np.delete(index,j,axis=0)
    
        ai = result[:,i]
        aj = result[:,j]
        temp = []
        for s,b in zip(ai,aj):
            bool_index = ai>aj
            for k in range(len(bool_index)):
                if k:
                    index[k, i] = index[k, j]
            temp.append(min(s,b))
        for k in range(len(temp)):
            result[k,i] = temp[k]
        result = np.delete(result,j,axis=1)
        index = np.delete(index,j,axis=1)
        return result, index
    
    def main(self, mat):
        '''

        Parameters
        ----------
        mat : array
            无向图的领接矩阵，可以是三角型矩阵.

        Returns
        -------
        Vt: list
            [[from_key, to_key]*n-1]
        Et: list
            [e1, ...,e(n-1)]

        '''
        result = copy.deepcopy(mat)
        Vt = []
        Et = []
        index = None
        while len(result) != 1:
            i,j = np.where(result==np.min(result[result>0]))
            i = i[0]
            j = j[0]
            if isinstance(index, np.ndarray):
                a,b = index[i,j]
                Vt.append([str(a+1), str(b+1)])
            else:
                Vt.append([str(i+1), str(j+1)])
            Et.append(np.min(result[result>0]))
            result,index = self.min_merge(result, i, j, index)
        return Vt, Et
    
    def draw(self, mat, Vt, Et):
         '''
         Parameters
         ----------
         graph : graph
             原图对象.
         Vt : graph
             Kruskal算法得出的.
         Returns
         -------
         plt.
         
         '''
         plt.rcParams['font.sans-serif'] = ['SimHei']
         plt.rcParams['axes.unicode_minus'] = False
         G = nx.Graph()
         GT = nx.Graph()
         num = '123456789'
         for i in range(len(mat)):
             for j in range(len(mat)):
                 if mat[i, j] != float('inf') and mat[i, j] != 0:
                     G.add_edge(num[i], num[j], weight=mat[i, j])
         for i,j in zip(Vt, Et):
             GT.add_edge(i[0], i[1], weight=j)
         pos = nx.spring_layout(G,seed=42)
         options = {
            "font_size": 20,
            "node_size": 200,
            "node_color": "green",
            "edgecolors": "white",
            "edge_color": 'blue',
            "font_color": 'red',
            "linewidths": 2,
            "width": 2,
            'alpha':0.8,
            'with_labels':True
            }
         plt.figure(figsize=(12,6))
         plt.subplot(121)
         nx.draw(G, pos, **options)
         plt.title('原图')
         plt.subplot(122)
         nx.draw(GT, pos, **options)
         plt.title('最小支撑树')
         plt.show()
            
        
        
    
if __name__ == '__main__':
    inf = float('inf')
    a = np.array([[0, 1, 12, inf, inf, inf],
                  [inf, 0, 9, 3, inf, inf],
                  [inf, inf, 0, inf, 5, inf],
                  [inf, inf, 4, 0, 13, 15],
                  [inf, inf, inf, inf, 0, 4],
                  [inf, inf, inf, inf, inf, 0]])
    s = Solution()
    Vt, Et = s.main(a)
    s.draw(a, Vt, Et)

• 结果如下：

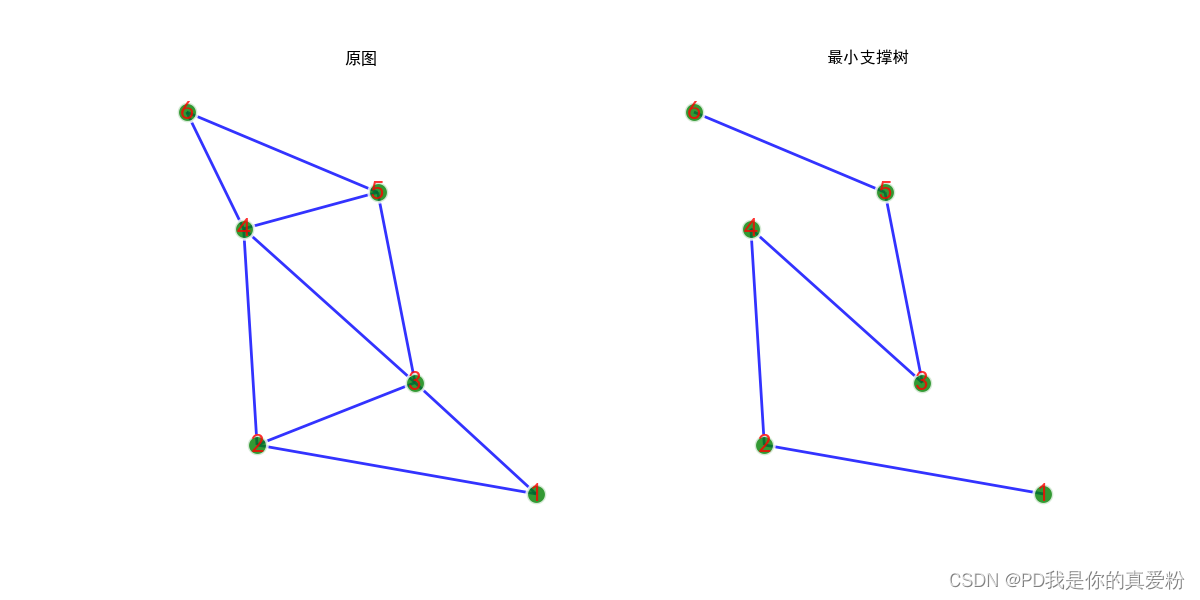
注意 博鲁夫卡算法是应用在无向图下的，考虑到无向图的连通分支判断过于简单，所以这里没有运用图的数据结构，直接操作矩阵就能得到结果，但是在算法过程中，注意两个点：

• 两个连通分支合并，对应矩阵上就是两行及两列取小后合并
• 维护好一个连通分支与其他连通分支的边是哪个节点提供的，而我们采用的方法就是维护一个index数组，这个数组的一行、一列代表一个连通分支，而第i行第j列的元素则表示第i个连通分支到第j个连通分支是哪两个点进行连接，比如
  $$index[2,4]=[4,6]$$

则表示第2个连通分支与第4个连通分支的最短边是节点4与节点6的边

最小瓶颈支撑树

定义

设$(G,W)$是无向连通赋权图，$G$的所有支撑树中权值最大的边权值最小的支撑树

从定义中可以看出，最小瓶颈支撑树不唯一，且可能不是最小支撑树

两者的关系：最小支撑树一定是最小瓶颈支撑树，最小瓶颈支撑树不一定是最小支撑树

斯坦纳树

设$(G=(V,E),W)$是无向连通赋权图，$R?V$,在G的所有包含$R$中所有顶点的子图中，总权值最小的树

特别地，当$R=V$时，斯坦纳树就是最小支撑树

注意 在斯坦纳树中，不一定只含有$R$，有时候多含有一些顶点可能树会更小

• 例如：对于 R = { A , B , C } R=\{A,B,C\} R={A,B,C}的斯坦纳树来说，当边权值不同时，斯坦纳树可能不同

事实上，斯坦纳树是NPC问题；

最小支撑树（下）就是这么多了，继续学习下一章吧！