堆排序前提
- 进行堆排序的数组是完全二叉树,本文章数组下标是从0开始计算的。如果第i个元素不是叶子节点,则其左孩子下标是i*2+1,右孩子下标是i*2+2;
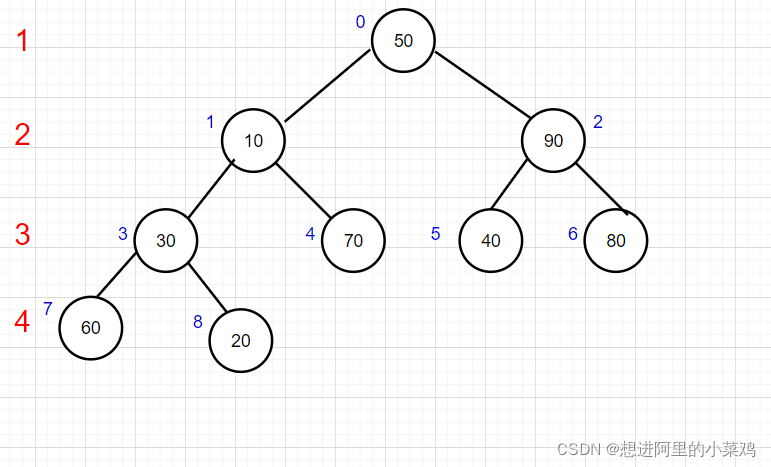
- 当前数组中最后一个非叶子的下标是array.leng/2-1。如下图节点30是最后一个非叶子节点。
???????????????
?生成大顶堆的思路
1.从最后一个非叶子节点30下标为3开始,将其左右节点中最大的与30交换,然后去遍历上一个非叶子节点90其下标为2,直到遍历到最后一个接点50为止。
2.当遍历到第二层的节点10时,其左右孩子中最大的为左孩子70需要将70和10交换,交换后下标为4的位置是10,其也要再次和左右孩子比较并交换;但是其没有左右孩子,就返回。
上面的第2点是对交换后下标i为什么等于2*i+1的原因,仔细看下第二点再去看代码就会懂了。
大顶堆的代码?
/**
* 数组下标从0开始,若下标为i,则其左孩子下标为i*2+1;右孩子是i*2+2;
*
* @param array 数组
* @param start 其实节点位置
* @param length 数组长度(二叉树节点个数)
*/
public static void Heapsort(int[] array, int start, int length) {
int temp = array[start];//交换节点用的。
for (int i = 2 * start + 1; i < length; i = i * 2 + 1) {
//在两个节点中找到最大一个和其父节点交换。
if (i + 1 < length && array[i] < array[i + 1]) {
i++;
}
if (array[i] > temp) {
//交换两个元素。将最大元素放到父节点处。
temp = array[start];
array[start] = array[i];
array[i] = temp;
//将当前节点位置移动到交换顺序的节点处,查看其交换后,其子节点是否还是完全二叉树,这也就是为什么i=i*2+1。
// 没有交换的节点其还是完全二叉树
start = i;
} else {
break;
}
}Heapsort(int[] array, int start, int length):start是开始遍历的节点下标,length是数组长度,为了后面的交换做准备。
找到下标start的节点temp的左孩子和右孩子中最大的一个,将其与下标start对应的节点比较:
①如果array[i]>temp,则交换;并且将父节点start移动到交换节点i处,接着处理交换后的节点start与其左右孩子的大小,此时的左孩子节点下标就是i*2+1,也就是循环的增加条件为什么是i=i*2+1。
②如果array[i]<temp的情况:原始的完全二叉树的左孩子必须大于其父节点,如果不大于说明已经交换完了,则退出循环。
接着就是遍历所有节点,变为大顶堆
//变为大顶堆
for (int i = array.length / 2 - 1; i >= 0; i--) {
Heapsort(array, i, array.length);
}
?堆排序思路
将得到的大顶堆中第0个元素,也就是最大的数,和数组最后的元素交换,并且继续堆排序去掉最后一个元素的数组。并将得到大顶堆的最大的元素和最后面的元素交换。
堆排序代码
//将大顶堆的头节点和最后的节点交换,将最大的数都放到最后,再次堆排序,此次堆排序的长度-1,
//排序完成后就得到了从小到大的数组
for (int i = array.length - 1; i > 0; i--) {
temp = array[0];
array[0] = array[i];
array[i] = temp;
Heapsort(array, 0, i);
}整体代码
package DataStructures.BinaryTree;
import java.util.Arrays;
/**
* @author :ALi
* @date :Created in 2021/12/10 19:31
* @description:堆排序
* @modified By:
* @version: $
*/
public class HeapsortTest {
public static void main(String[] args) {
int[] array = {50, 10, 90, 30, 70, 40, 80, 60, 20};
int temp = 0;
//变为大顶堆
for (int i = array.length / 2 - 1; i >= 0; i--) {
Heapsort(array, i, array.length);
}
//将大顶堆的头节点和最后的节点交换,将最大的数都放到最后,再次堆排序,此次堆排序的长度-1,
//排序完成后就得到了从小到大的数组
for (int i = array.length - 1; i > 0; i--) {
temp = array[0];
array[0] = array[i];
array[i] = temp;
Heapsort(array, 0, i);
}
System.out.println(Arrays.toString(array));
}
/**
* 数组下标从0开始,若下标为i,则其左孩子下标为i*2+1;右孩子是i*2+2;
*
* @param array 数组
* @param start 其实节点位置
* @param length 数组长度(二叉树节点个数)
*/
public static void Heapsort(int[] array, int start, int length) {
int temp = array[start];
for (int i = 2 * start + 1; i < length; i = i * 2 + 1) {
//在两个节点中找到最大一个和其父节点交换。
if (i + 1 < length && array[i] < array[i + 1]) {
i++;
}
if (array[i] > temp) {
//交换两个元素。将最大元素放到父节点处。
temp = array[start];
array[start] = array[i];
array[i] = temp;
//将当前节点位置移动到交换顺序的节点处,查看其交换后,其子节点是否还是完全二叉树,这也就是为什么i=i*2+1。
// 没有交换的节点其还是完全二叉树
start = i;
} else {
break;
}
}
}
}