「图解大厂面试高频算法题」动态规划-最大正方形

题目原链接: https://leetcode-cn.com/problems/maximal-square/

题目介绍

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例1

在这里插入图片描述

输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

示例2

在这里插入图片描述

输入：matrix = [[“0”,“1”],[“1”,“0”]]
输出：1

题目解答

方法一：二维动态规划

思路和算法

我们可以使用动态规划的方法来解决这个问题，创建一个二维数组dp， dp[i][j]表示以matrix[i][j]为右下角，且只包含1的正方形的边长的最大值，如果我们能计算出所有dp的值，那么最大的正方形面积就为max(dp[i][j])的平方了。现在最关键的问题就是我们如何计算出dp[i][j]的值。
在这里插入图片描述

如果matrix[i][j]=0，那很好理解dp[i][j]=0。
如果matrix[i][j]=1，dp[i][j]如何计算呢？请看上图，图中有三个正方形：
- 蓝色正方形的边长为4，dp数组下标为dp[i-1][j-1]。
- 绿色正方形的边长为2，dp数组下标为dp[i-1][j]。
- 黄色正方形的边长为3，dp数组下标为dp[i][j-1]。
  我们从上图中可以看出dp[i][j]的值为3，取决于左上方dp[i-1][j-1]，正上方dp[i-1][j]，正左方dp[i][j-1]这三个值中最小的一个值再加1，得出状态转移方程为dp[i][j] = min(dp[i-1][j-1], dp[i-1][j],dp[i][j-1])+1。
  那么我们该如何去理解这个表达式呢？可以这样理解：
绿色正方形(dp[i-1][j])表示：可以为以dp[i][j]为右下角的正方形的右边提供边长为2的边。
黄色正方形(dp[i][j-1])表示：可以为以dp[i][j]为右下角的正方形的下边提供边长为3的边。
蓝色正方形(dp[i-1][j-1])表示：可以为以dp[i][j]为右下角的正方形的左边和上边提供边长为4的边。
取三者中的最小值(min(dp[i-1][j-1], dp[i-1][j],dp[i][j-1]))是因为根据木桶原理，我们只能取最短的一个边来作为dp[i][j]表示的最大的正方形的边。
加上matrix[i][j]本身的这个正方形的边长1，就得到了以dp[i][j]为右下角最大的正方形的边长。

具体例子讲解

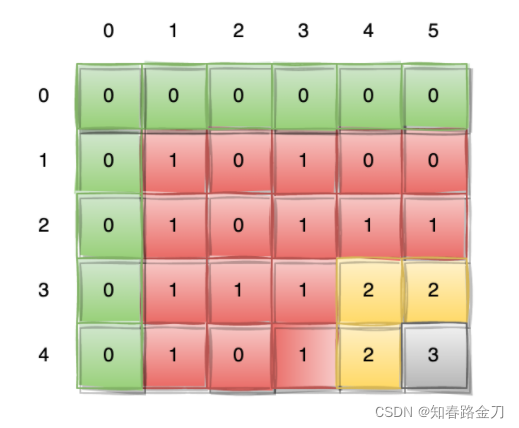
给出一个M=4，N=5的一个matrix。
在这里插入图片描述

绿色表示哨兵，我们不需要对这些dp进行计算。
灰色方格表示当前正在计算的dp[i][j]。
黄色方格是计算dp[i][j]所依赖的dp[i-1][j-1]，dp[i-1][j]，dp[i][j-1]。

根据状态转移方程我们可以算出dp[3][4] = min(dp[2][3], dp[2][4], dp[3][3]) + 1 = 2，
同理dp[3][5]=2，dp[4][4]=2。
在这里插入图片描述
dp[4][5] = min(dp[4][4], dp[3][4], dp[3][5]) + 1 = 3

代码实现

class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return 0;
        }
        int M = matrix.length;
        int N = matrix[0].length;
        int[][] dp = new int[M+1][N+1];
        int result = 0;
        for (int i = 1; i <= M; i++) {
            for (int j = 1; j <= N; j++) {
                if (matrix[i-1][j-1] == '0') {
                    continue;
                }
                dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1])) + 1;
                result = Math.max(result, dp[i][j]);
            }
        }
        return result*result;
    }
}

复杂度分析

时间复杂度：O(MN)
空间复杂度：O(MN)

方法二：一维动态规划

思路和算法

有一个更优的解法，因为在二维动态规划的实现中dp[i][j]总是以从左到右，从上到下的方向来计算的，所以我们可以对二维数组进行化简变成一维数组，只需要一个prev变量来临时存储dp[i][j-1]。状态转移方程就变为了dp[j] = min(dp[j-1], dp[j], prev) + 1。

dp[j-1]表示二维数组中的dp[i-1][j-1]。
dp[j]表示二维数组中的dp[i-1][j]。
prev 表示二维数组中的dp[i][j-1]。

代码实现

class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0) {
                return 0;
        }
        int M = matrix.length;
        int N = matrix[0].length;
        int[] dp = new int[N+1];
        int result = 0;
        for (int i = 1; i <= M; i++) {
            int prev = 0;
            for (int j = 1; j <= N; j++) {
                int t = dp[j];
                if (matrix[i-1][j-1] == '0') {
                    dp[j] = 0;
                    continue;
                }
                dp[j] = Math.min(dp[j-1], Math.min(dp[j], prev)) + 1;
                prev = t;
                result = Math.max(result, dp[j]);
            }
        }
        return result*result;
    }
}