剑指 Offer 46. 把数字翻译成字符串

题目描述

给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

提示：

$0 <= num < 2^{31}$

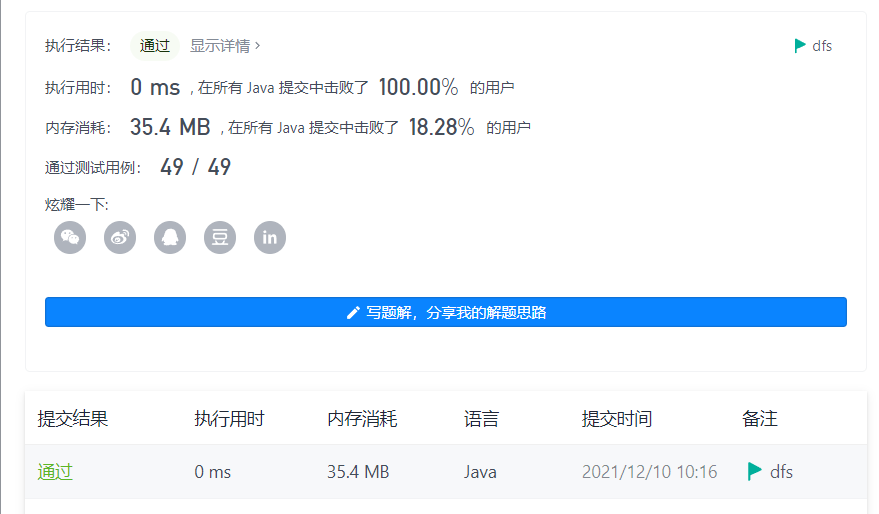
DFS

题目中说了 $0 <= num < 2^{31}$ ，即 $n u m$ 最多也就 10 位，所以可以考虑使用 dfs。

思路：

每次可以取 1 位或者 2 位数字，直到取到叶子节点截止。
每次取数字的前提条件：
- 取一位数字时：没有限制，所有只含 1 位的都满足；
- 取2位数字时，限制条件为：这2位构成的数字必须在 [0, 26) 之间：

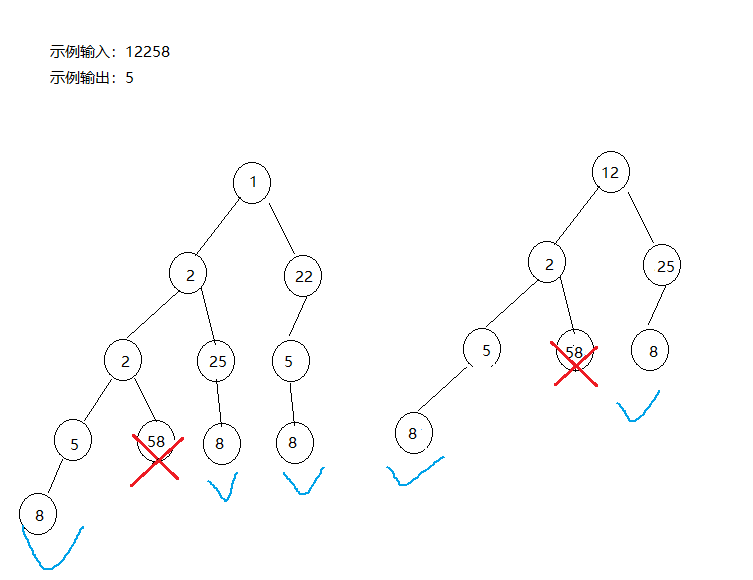
以示例输入 $n u m = 12258$ 为例，其 dfs 过程如下所示：
dfs-剑指 Offer 46. 把数字翻译成字符串

class Solution {
    int res = 0;
    
    public int translateNum(int num) {
        dfs(Integer.toString(num), 0);
        return res;
    }

    public void dfs(String s, int startIndex) {
        if (startIndex >= s.length()) {
            res++;
            return;
        }
        // 取一个字符
        dfs(s, startIndex + 1);
        // 取2个字符
        if (s.charAt(startIndex) <= '2' && startIndex + 1 < s.length() && (s.charAt(startIndex) == '1'
                || (s.charAt(startIndex) == '2' && s.charAt(startIndex + 1) < '6'))) { // 数字必须在 [0, 25] 之间
            // System.out.println("testing...");
            dfs(s, startIndex + 2);
        }
    }
}

时间复杂度： $O(2^n)$ （每个节点1次 * 所有节点个数）
空间复杂度： $O (n)$ （递归用的栈是二叉树的高度）

其中，这里 n 为 nums 的 “位数”，
dfs

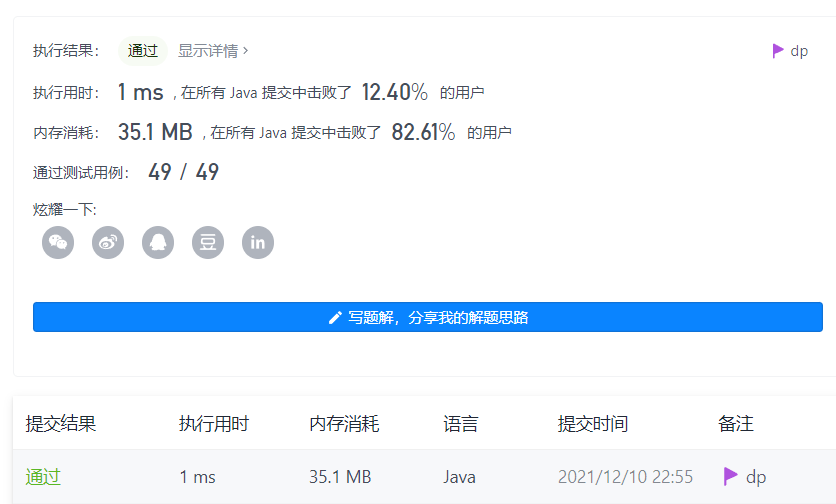
dp

参考 K佬题解
思路：

dp[i]表示以i结尾的所有翻译方法
递推公式
- 如果最近2个字符构成的数字在 [0, 25] 中，可以翻译。此时，dp[i] = dp[i - 1] + dp[i - 2];
- 如果只能翻译1个字符，则 dp[i] = dp[i - 1];
初始化
- dp[1] = 1; // 1个数字只有一种翻译方法
- dp[0] = 1; // 若2个数字可以翻译，则 dp[2] = dp[0] + dp[1] = 2，且dp[1] = 1，所以dp[0] = 1

class Solution {
    public int translateNum(int num) {
        String s = Integer.toString(num);
        int n = s.length();
        int[] dp = new int[n + 1];  // dp[i]表示以i结尾的所有翻译方法
        // 3、初始化
        dp[0] = 1; // 若2个数字可以翻译，则 dp[2] = dp[0] + dp[1] = 2，且dp[1] = 1，所以dp[0] = 1
        dp[1] = 1; // 1个数字只有一种翻译方法
        // 4、遍历顺序（由递归公式可知，从左到右）
        for (int i = 2; i <= n; i++) {
            // 2、递推公式
            if (s.charAt(i - 2) == '1' || (s.charAt(i - 2) == '2' && s.charAt(i - 1) < '6')) { // 如果最近2个字符构成的数字在 [0, 25] 中，可以翻译
                dp[i] = dp[i - 1] + dp[i - 2];
            } else { // 只有当前s[i]一个可以翻译
                dp[i] = dp[i - 1];
            }
        }
        // 5、打印dp
        System.out.println(Arrays.toString(dp));
        return dp[n];
    }
}