声明:本博客仅为本人学习途中做的笔记 采自青岛大学王卓老师的视频教学 主要内容为算法思路,具体代码实现还需修改后才能运行,望各位看官多多包涵,您的点赞与评论是对我最大的肯定!
1.图的定义和基本术语
图:G=(V,E)
V:顶点(数据元素)的有穷非空集合
G:边的有穷集合
无向图:每条边都是无方向的
有向图:每条边都是有方向的
完全图:任意两个点都有一条边相连
稀疏图:有很少边或弧的图(e<nlogn)
稠密图:有较多边或弧的图
网:边/弧带权的图
邻接:有边/弧相连的两个顶点之间的联系
存在(vi,vj),则称vi和vj互为邻接点
存在<vi,vj>,则称vi邻接到vj,vj邻接于vi
关联(依附):边/弧与顶点之间的关系
存在(vi,vj)/<vi,vj>,则称该边/弧关联于vi和vj
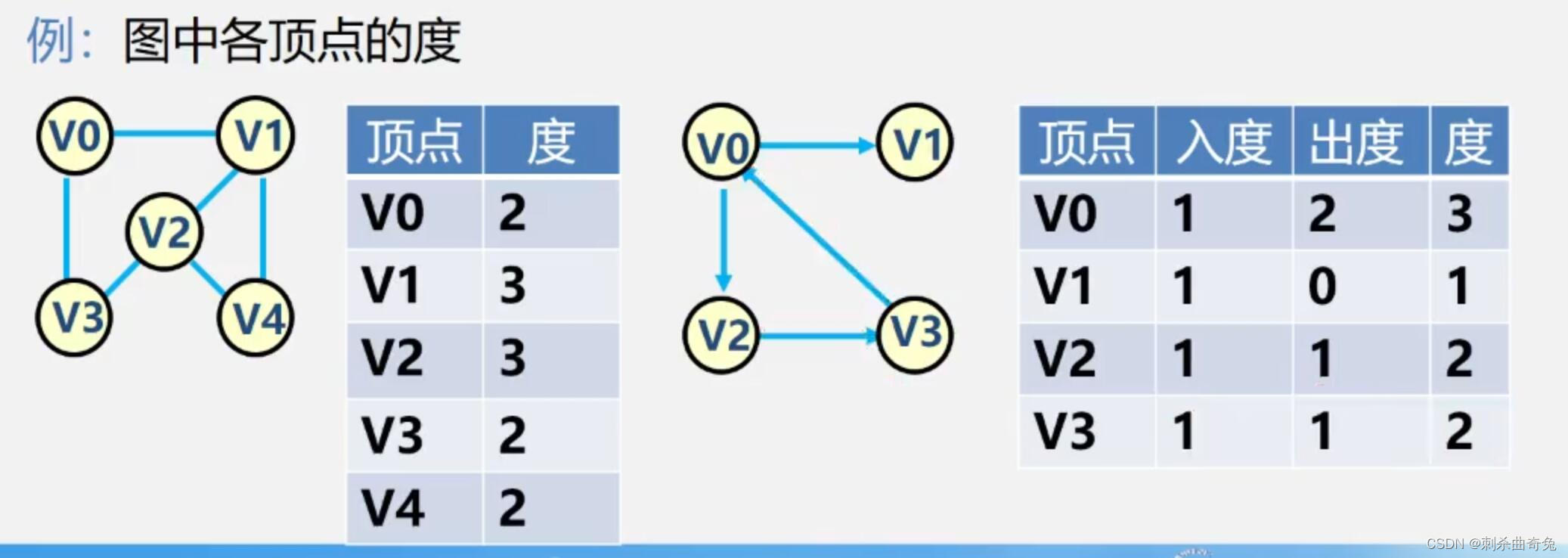
顶点的度:与该顶点相关联的边的数目,记为TD(v)
在有向图中,顶点的度等于该顶点的入度与出度之和。
顶点v的入度是以v为终点的有向边的条数,记作ID(v)
顶点v的出度是以v为始点的有向边的条数,记作OD(v)
路径:接续的边构成的顶点序列
路径长度:路径上边或弧的数目/权值之和。
回路(环):第一个顶点和最后一个顶点相同的路径。
简单路径:除路径起点和终点可以相同外,其余顶点均不相同的路径
简单回路(简单环):除路径起点和终点相同外,其余顶点均不相同的路径。
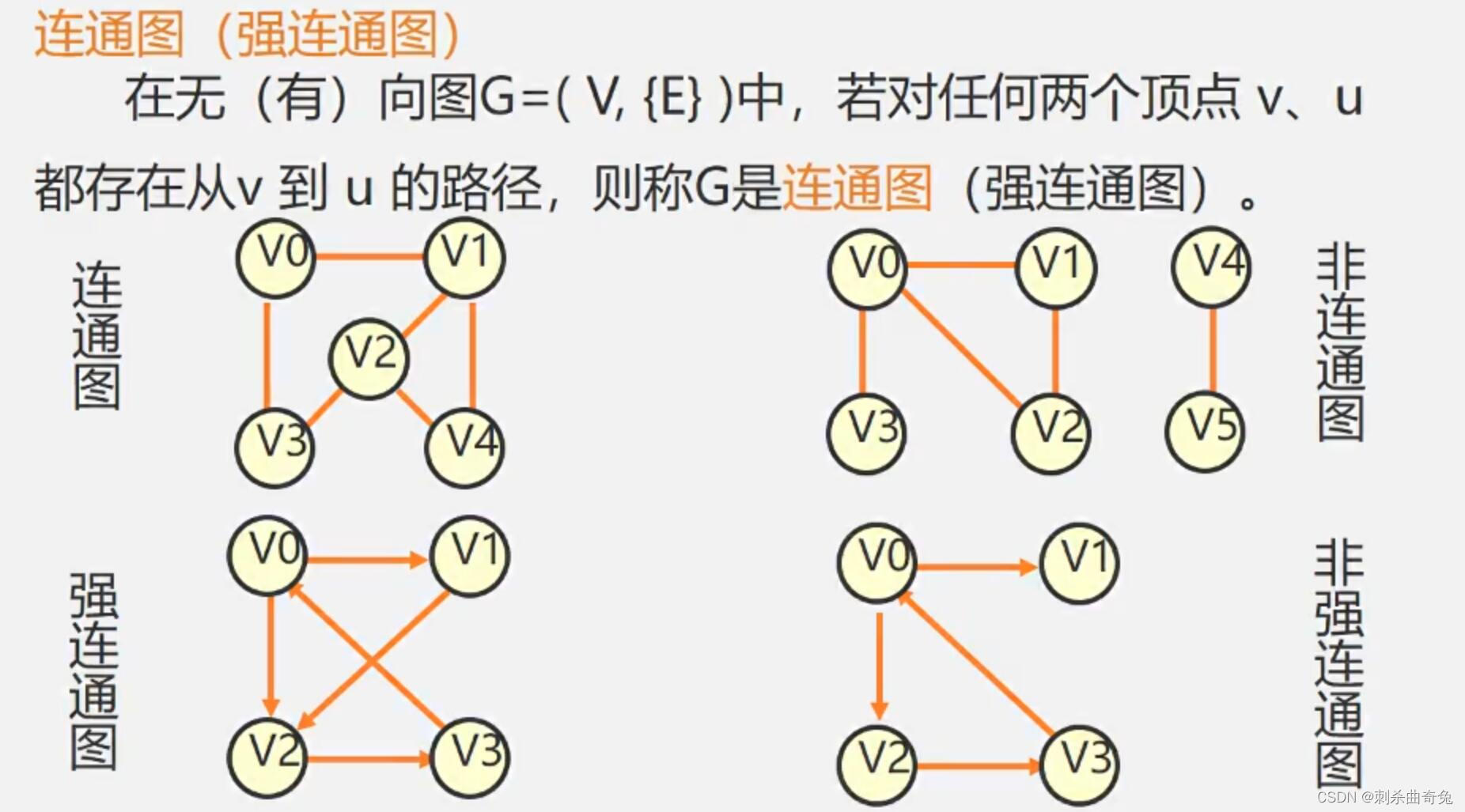
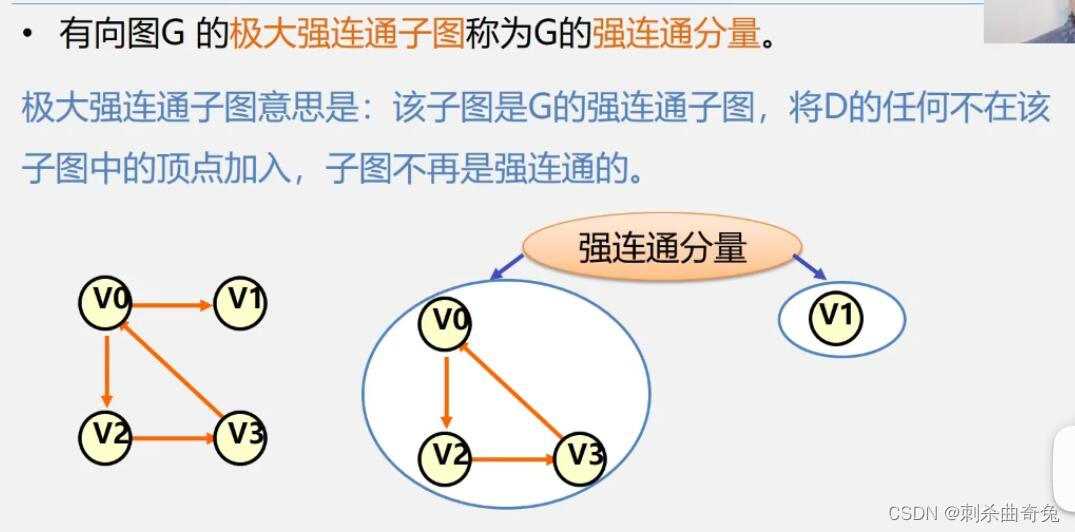
有向图中,若任意两个顶点 Vi 和 Vj,满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通,也就是都含有至少一条通路,则称此有向图为强连通图。
权与网:图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。 带权的图称为网。
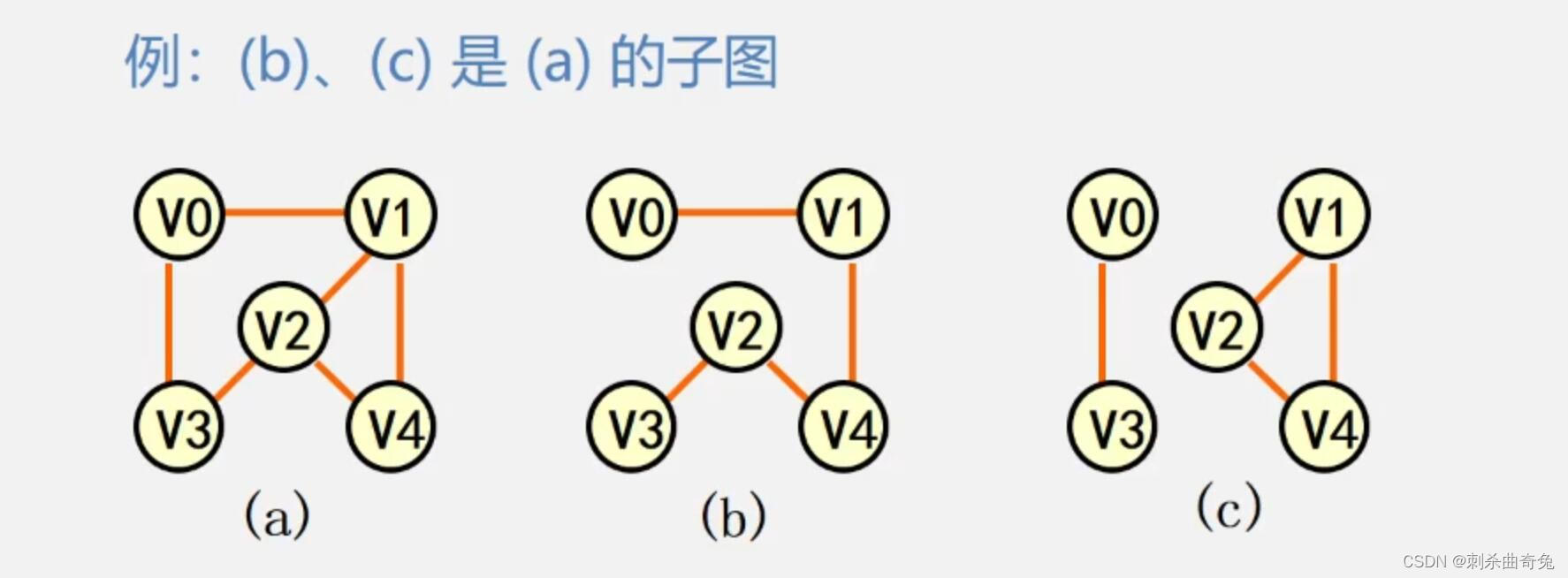
子图:设有两个图G=(V,{E})、G1= (V1,{E1}),若V1
∈
\in
∈ V,E1
∈
\in
∈ E,则称G1是G的子图。
连通分量(强连通分量):无向图G的极大连通子图称为G的连通分量。
极大连通子图意思是:该子图是G连通子图,将G的 任何不在该子图中的顶点加入,子图不再连通。
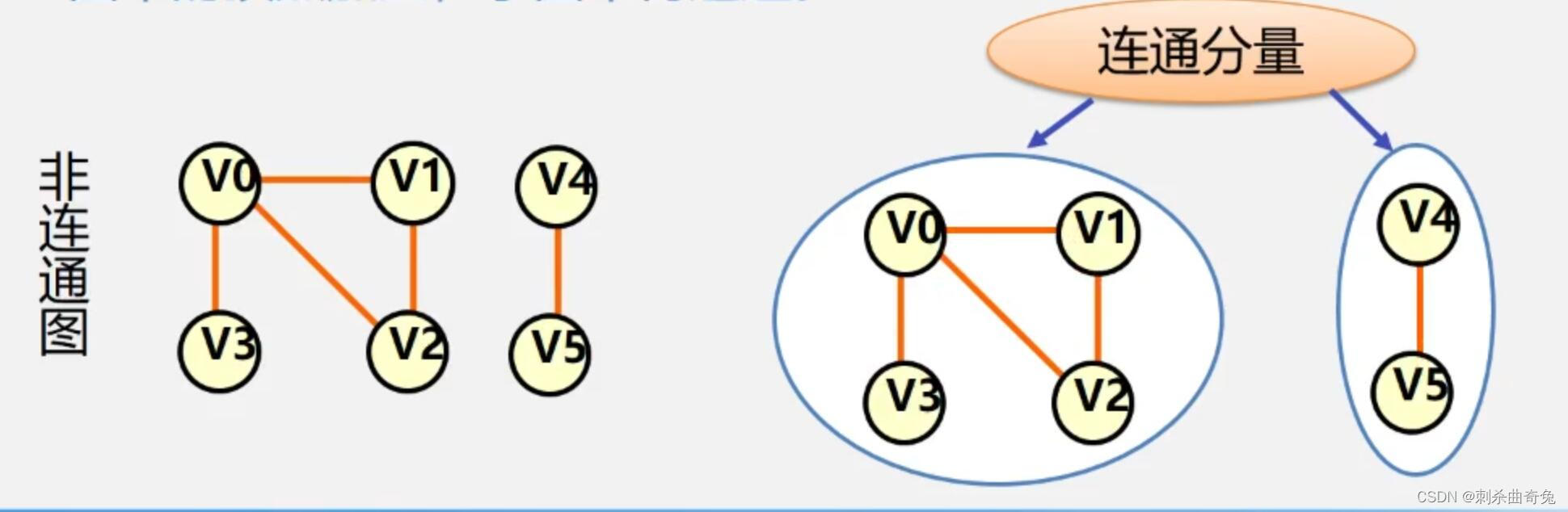
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,子图不再连通。
生成树:包含无向图G所有顶点的极小连通子图。(不存在回路)
生成森林:对非连通图,由各个连通分量的生成树的集合。
2.图的存储结构
图的逻辑结构:多对多
图没有顺序存储结构,但可以借二维数组来表示元素间的关系
数组表示法:邻接矩阵
链式存储结构:多重链表 --> 邻接表、邻接多重表、十字链表
重点介绍:邻接矩阵(数组)表示法、邻接表(链式)表示法
邻接矩阵
1、数组(邻接矩阵)表示法
建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各顶点间关系)
设图A=(V,E)有n个顶点,则
顶点表Vexs[n]
| i | 0 | 1 | 2 | … | n-1 |
|---|---|---|---|---|---|
| Vexs[i] | v1 | v2 | v3 | … | vn |
图的邻接矩阵是一个二维数组A.arcs[n] [n],定义为:
A
.
a
r
c
s
[
i
]
[
j
]
=
{
1
,
如
果
<
i
,
j
>
∈
E
?
或
者
(
i
,
j
)
∈
E
0
,
否
则
A.arcs [i][j]= \begin{cases} 1,\qquad\qquad如果<i,j>\in E \,或者(i,j)\in E\\ 0,\qquad\qquad否则 \end{cases}
A.arcs[i][j]={1,如果<i,j>∈E或者(i,j)∈E0,否则?

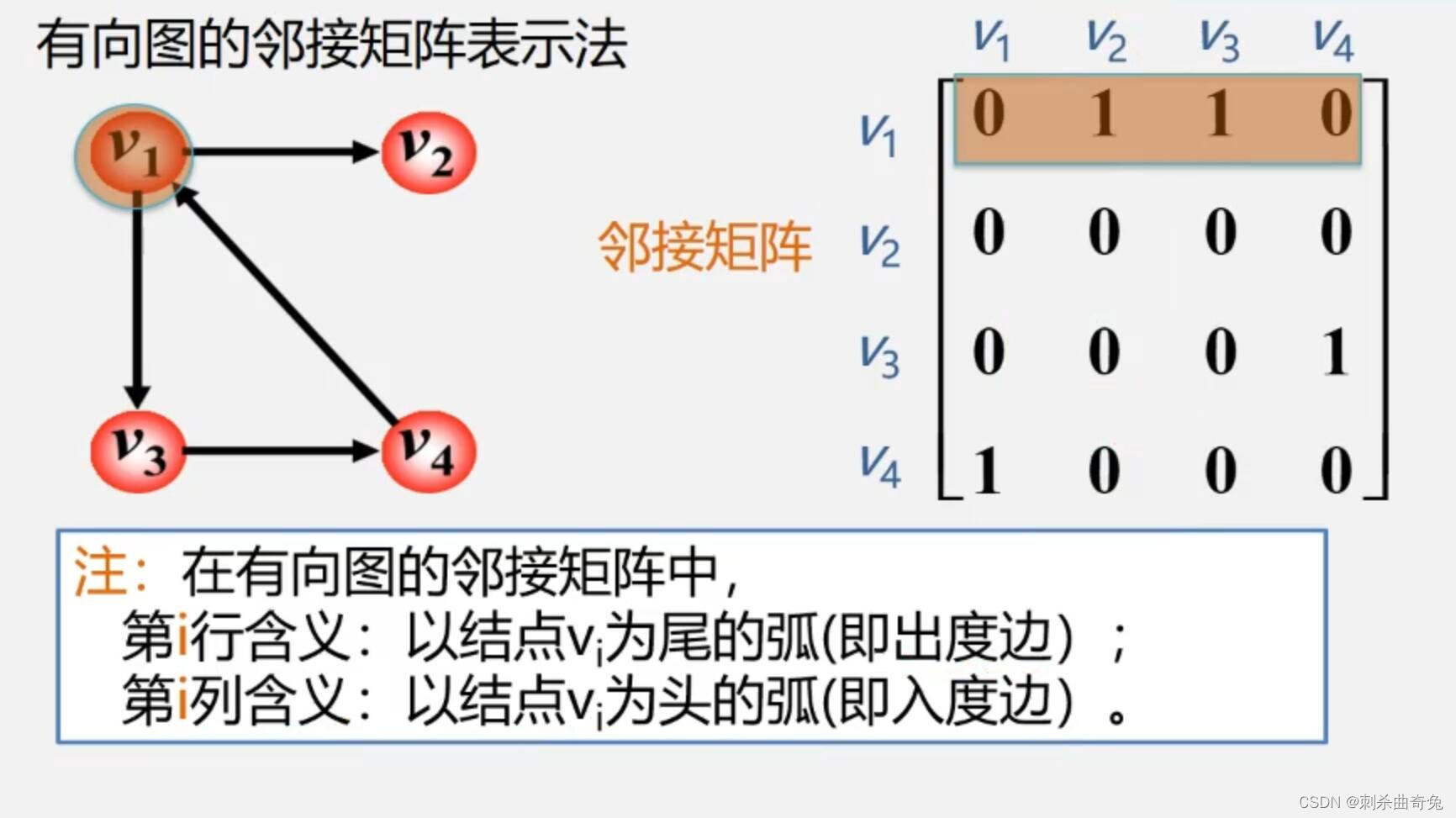
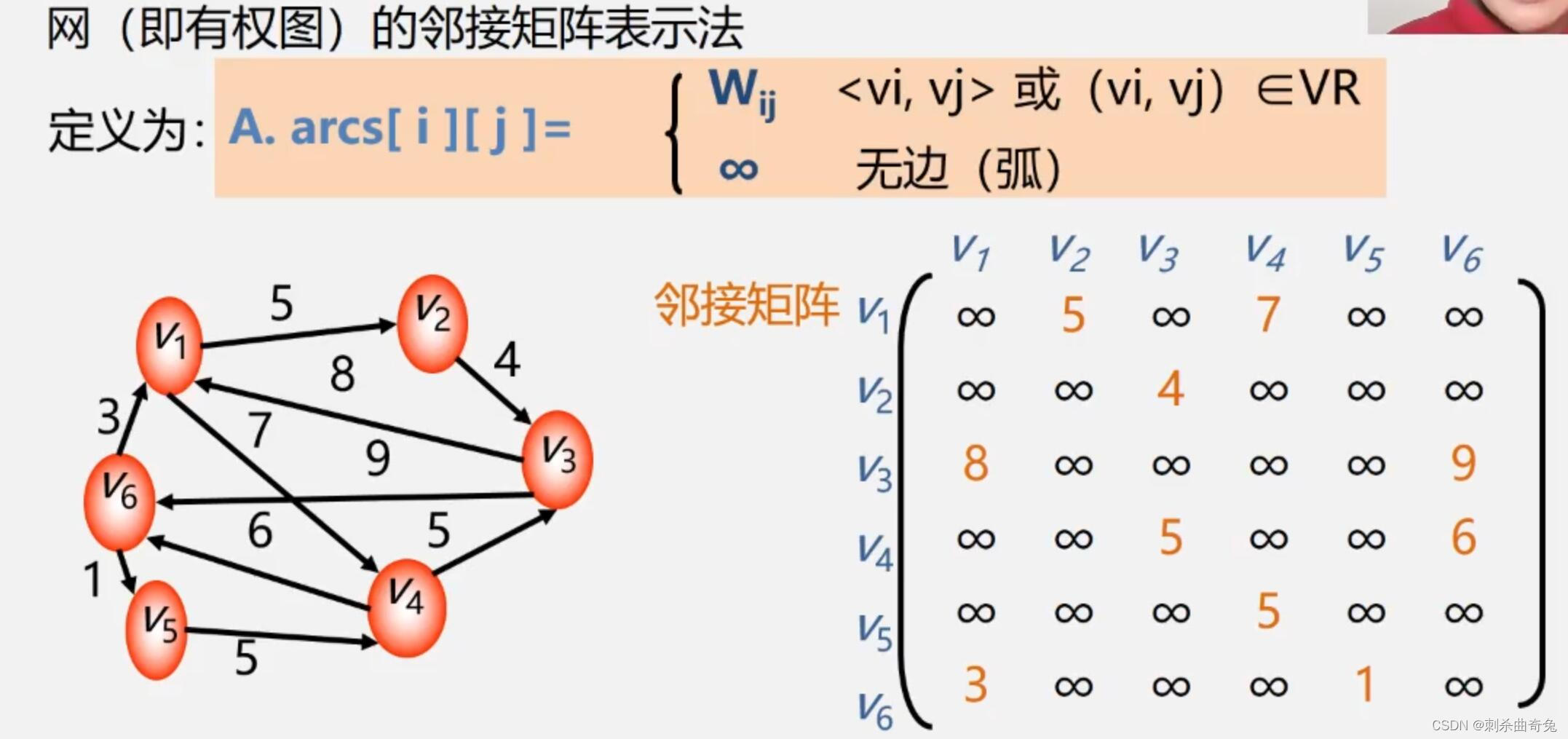
邻接矩阵的存储表示:用两个数组分别存储顶点表和邻接矩阵
#define Maxlnt 32767 //表示极大值,即oo
#define MVNum 100 //最大顶点数
typedef char VerTexType; //设顶点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型
typedef struct{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //图的当前点数和边数
}AMGraph; // Adjacency Matrix Graph
采用邻接矩阵表示法创建无向网
Status CreateUDN(AMGraph &G){
//采用邻接矩阵表示法,创建无向网G
cin> >G.vexnum> >G.arcnum;//输入总顶点数,总边数
for(i = 0; i<G.vexnum; ++i)
cin>>G.vexs[i];
//依次输入点的信息
for(i = o; i<G.vexnum;++i)//初始化邻接矩阵
for(j = 0; j<G.vexnum;++j)
G.arcs[i]j] = Maxlnt;//边的权值均置为极大值
for(k = 0; k<G.arcnum;++k){//构造邻接矩阵
cin> >v1> >v2> >w;
//输入一条边所依附的顶点及边的权值
i = LocateVex(G, v1);
j = LocateVex(G, v2);//确定v1和v2在G中的位置
G.arcs[i][j] = w; //边<v1,v2>的权值置为w
G.arcsj][1i]= G.arcs[i][j];
//置<v1, v2>的对称边<v2,v1>的权值为w
}//for
return OK;
}//CreateUDN
补充算法:在图中查找顶点
int LocateVex(AMGraph G, VertexType u) {
//图G中查找顶点u,存在则返回顶点表中的下标;否则返回-1
int i;
for(i=O;i<G.vexnum;++i)
if(u==G.vexs[i]) return i;
return -1;
}
2、采用邻接矩阵表示法创建无向网
(1)输入总顶点数和总边数。
(2)依次输入点的信息存入顶点表中。
(3)初始化邻接矩阵,使每个权值初始化为极大值。
(4)构造邻接矩阵。
邻接表
1、邻接表示法(链式)
无向图
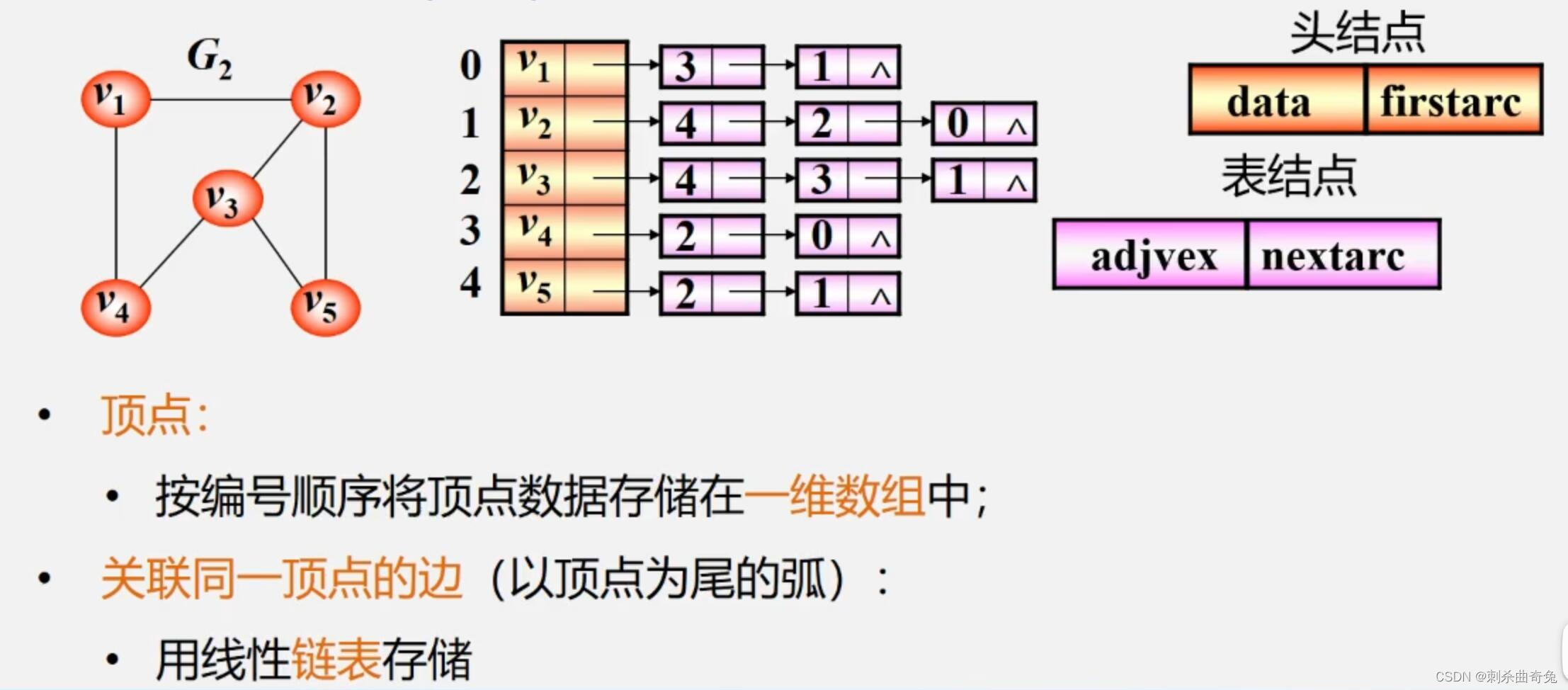
特点:
邻接表不唯一
若无向图中有n个顶点、e条边则其邻接表需n个头结点和2e个表结点
无向图中顶点vi的度为第i个单链表中的结点数
有向图
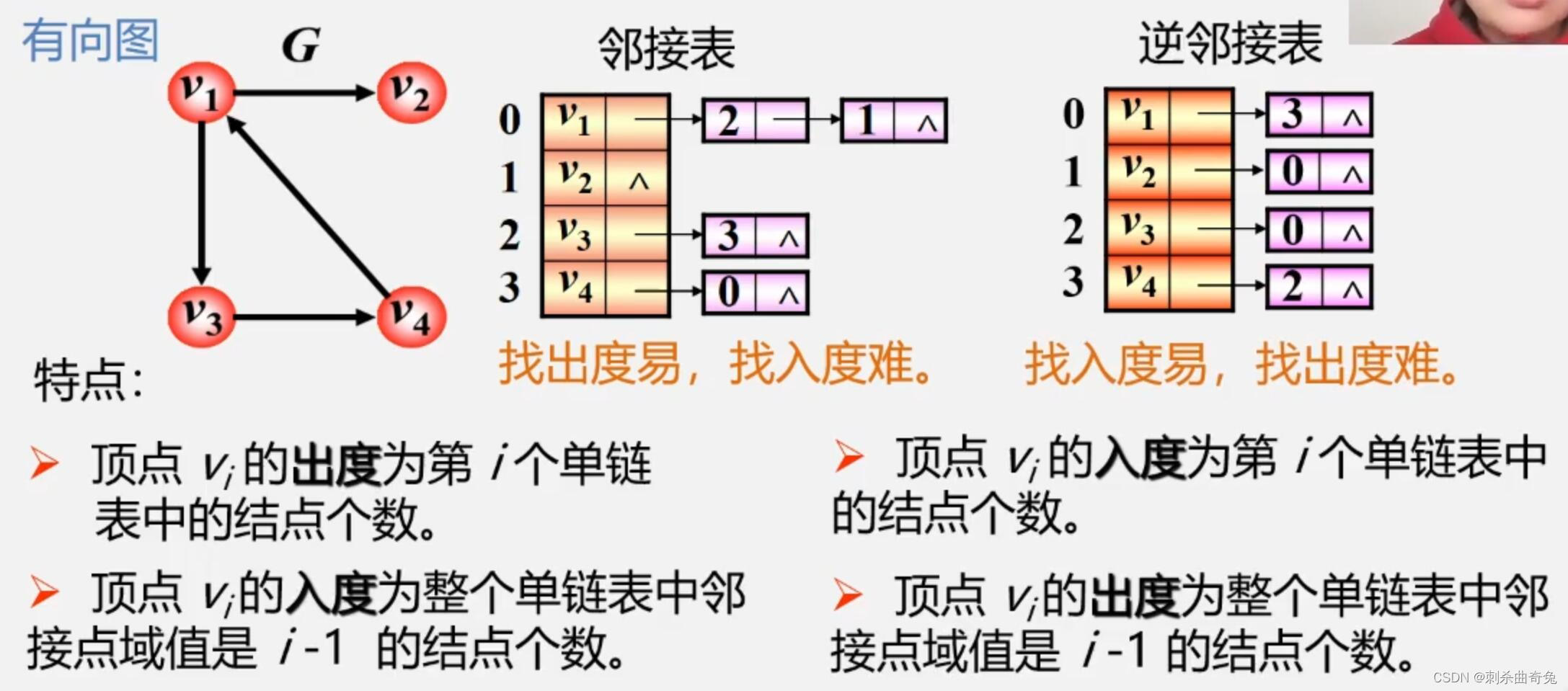
图的邻接表存储表示:
顶点表
typedef struct VNode{
VerTexType data; //顶点信息
ArcNode *firstarc; //指向第一条依附该顶点的指针
}VNode,AdjList[MVNum]; //AdjList表示邻接表类型
弧(边)的结点结构 单链表
#define MVNum 100 //最大顶点数
typedef struct ArcNode{ //边结点
int adjvex; //该边所指向的顶点的位置
struct ArcNode *nextarc; //指向下一条边的指针
Otherlnfo info; //和边相关的信息
}ArcNode;
图的结构定义
typedef struct{
AdjList vertices; //vertices--vertes的复数
int vexnum,arcnum; //图的当前顶点数和弧数
}ALGraph;
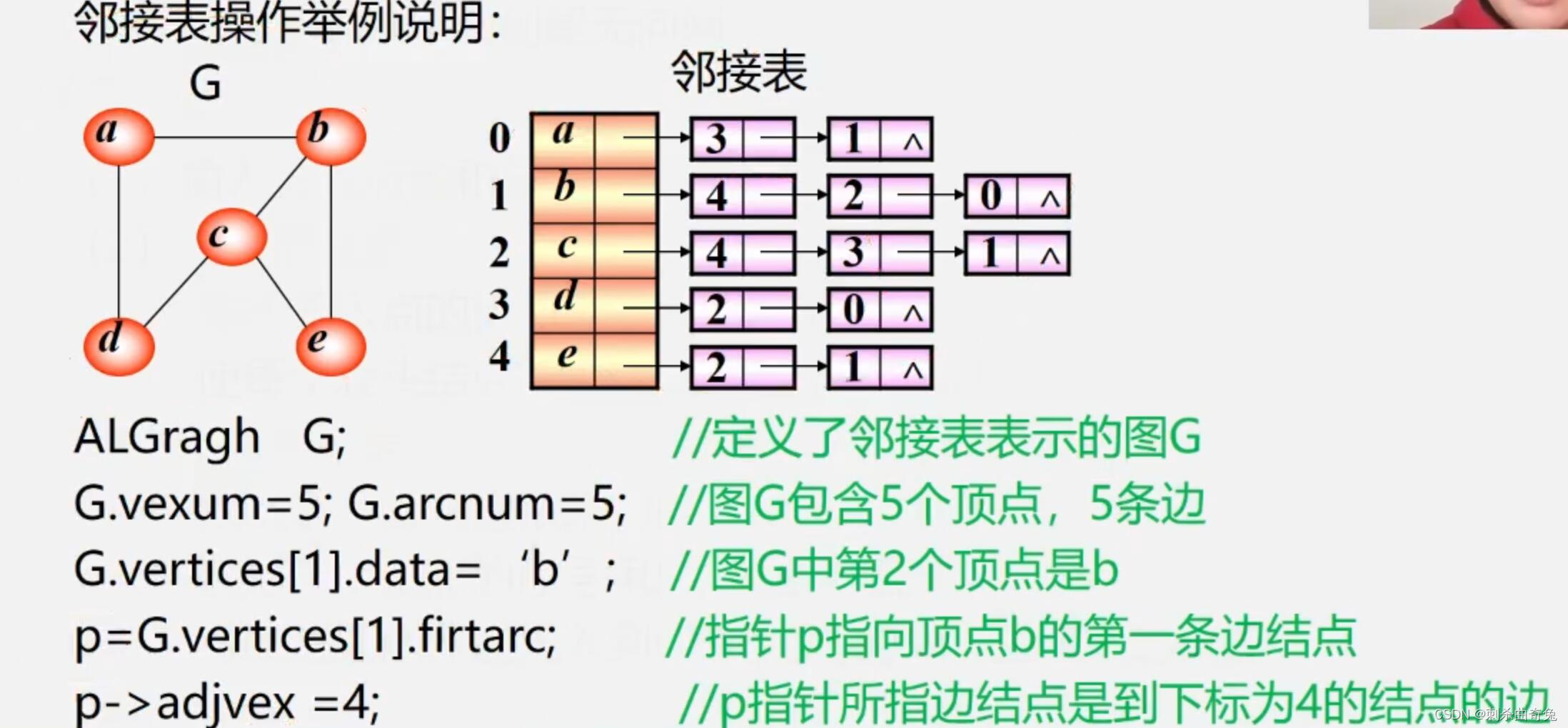
2、采用邻接表表示法创建无向网
算法思想
(1)输入总顶点数和总边数。
(2)建立顶点表
依次输入点的信息存入顶点表中
使每个表头结点的指针域初始化为NULL
(3)创建邻接表
依次输入每条边依附的两个顶点确定两个顶点的序号i和j,建立边结点
将此边结点分别插入到v,和v;对应的两个边链表的头部
利用邻接表表示法创建无向网
Status CreateUDG(ALGraph &G){
//采用邻接表表示法,创建无向图G
cin> >G.vexnum>>G.arcnum;//输入总顶点数,总边数
for(i = O; i<G.vexnum; ++i){
//输入各点,构造表头结点表
cin> >G.vertices[i].data;//输入顶点值
G.vertices[i].firstarc=NULL;
//初始化表头结点的指针域
}//for
for(k = O; k<G.arcnum;++k){//输入各边,构造邻接表
cin>>v1>>v2; //输入一条边依附的两个顶点
i = LocateVex(G, v1);
j = LocateVex(G, v2);
p1=new ArcNode; //生成一个新的边结点*p1
p1->adjvex=j; //邻接点序号为j
p1->nextarc= G.vertices[i].firstarc;
G.vertices[i].firstarc=p1;
//将新结点*p1插入顶点vi的边表头部
p2=new ArcNode; //生成另一个对称的新的边结点*p2
p2->adjvex=i; //邻接点序号为i
p2->nextarc= G.vertices[j].firstarc;
G.vertices[j].firstarc=p2;
//将新结点*p2插入顶点vj的边表头部
}
return OK;
}
十字链表–用于有向图
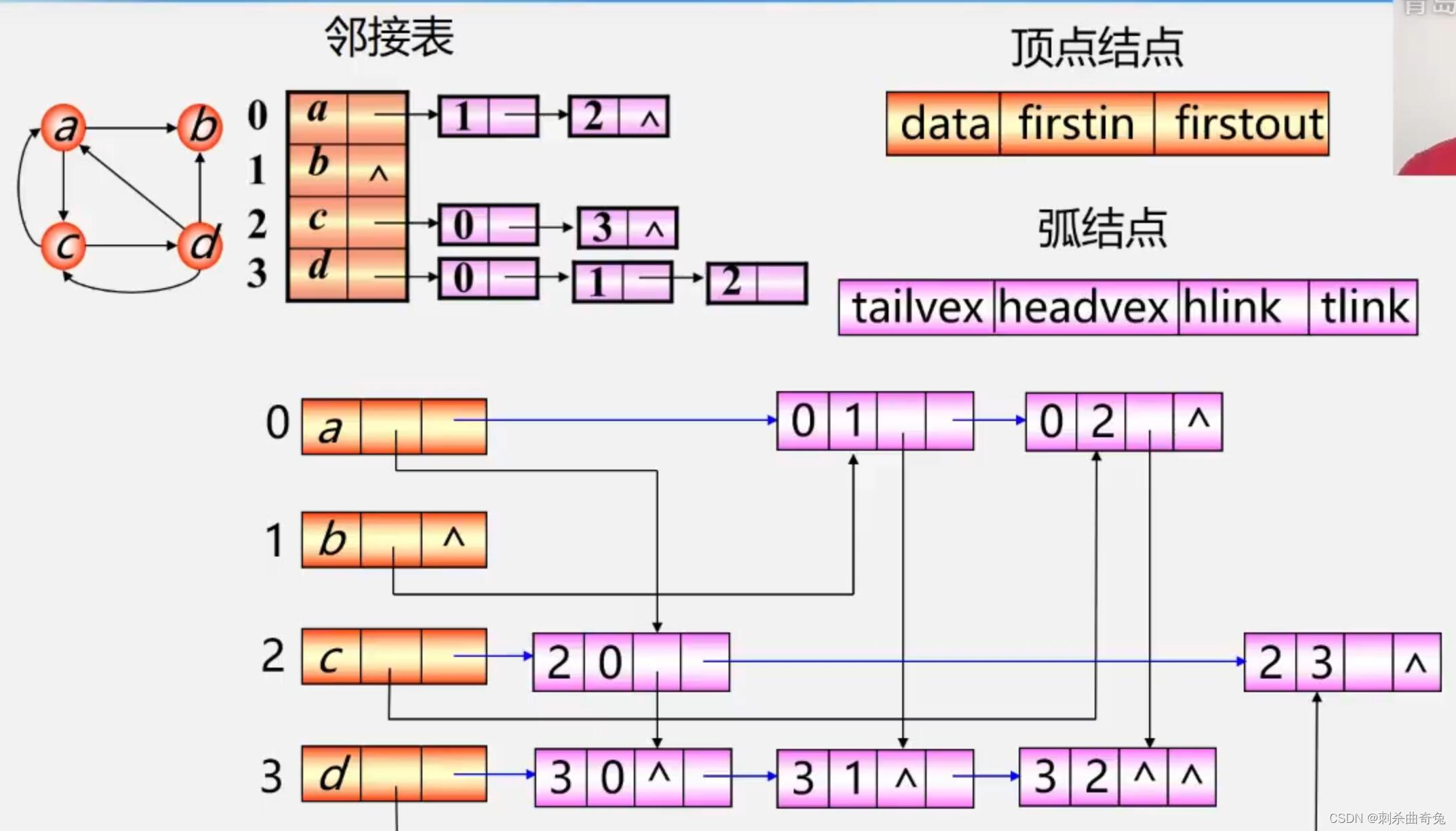
邻接多重表–用于无向图
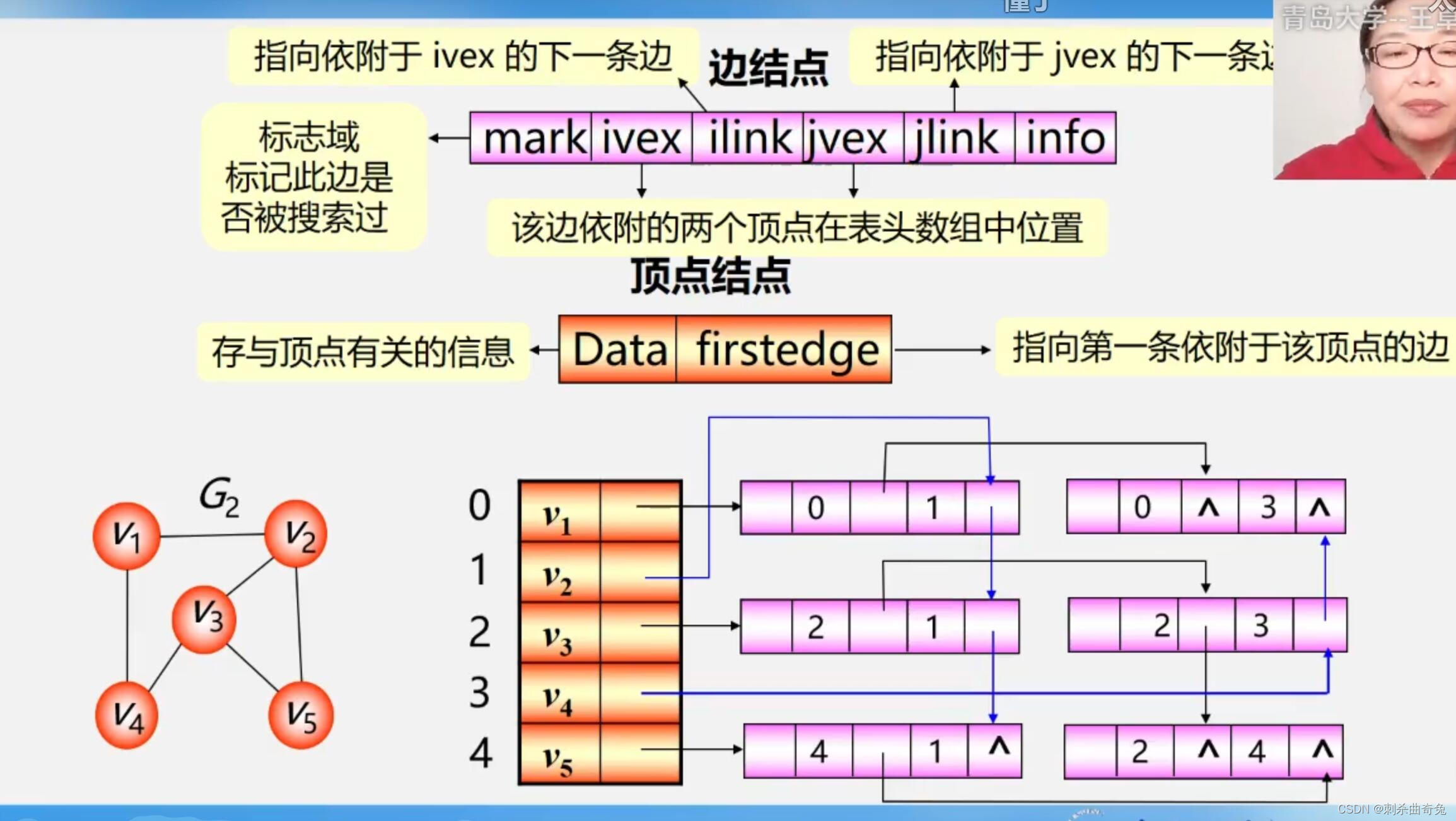
3.图的遍历
从已给的连通图中某一顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访问一次,就叫做图的遍历,它是图的基本运算。
遍历实质:找每个顶点的邻接点的过程
图的特点
图中可能存在回路,且图的任一顶点都可能与其它顶点相通,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。
怎样避免重复访问?
解决思路:设置辅助数组visited [n],用来标记每个被访问过的顶点。
初始状态visited [i]为0
顶点i被访问,改visited [i]为1,防止被多次访问
深度优先遍历(DFS)
- 在访问图中某一起始顶点v后,由v出发,访问它的任一邻接顶点w;
- 再从w出发,访问与w邻接但还未被访问过的顶点W2;
- 然后再从w2出发,进行类似的访问,
- 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点u为止。
- 接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。
- 如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;
- 如果没有,就再退回一步进行搜索重复上述过程,直到连通图中
所有顶点都被访问过为止。
深度优先搜索遍历算法实现
采用邻接矩阵表示图的深度优先搜索遍历
void DFS(AMGraph G, int v){ //图G为邻接矩阵类型
cout<<v; visited[v] = true; //访问第v个顶点
for(w=0;w<G.vexnum;w++)//依次检查邻接矩阵v所在的行
if((G.arcs[v][w]!=0)&&(!visited[w]))
DFS(G, w);
//w是v的邻接点,如果w未访问,则递归调用DFS
}
广度优先搜索(BFS)
方法:从图的某一结点出发,首先依次访问该结点的所有邻接点Vi1, Vi2,…Vin,再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点
重复此过程,直至所有顶点均被访问为止。
按广度优先非递归遍历连通图G
void BFS (Graph G, int v){//按广度优先非递归遍历连通图G
cout<<v; visited[v] = true;//访问第v个顶点
lnitQueue(Q); //辅助队列Q初始化,置空
EnQueue(Q, v); //v进队
while(!QueueEmpty(Q)){//队列非空
DeQueue(Q, u); //队头元素出队并置为u
for(w=FirstAdjVex(G,u);w>=O;w=NextAdjVex(G, u,w))
if(!visited[w]){//w为u的尚未访问的邻接顶点
cout<<w;
visited[w] = true;
EnQueue(Q, w);//w进队
}//if
}//while
}//BFS
4.图的应用
最小生成树
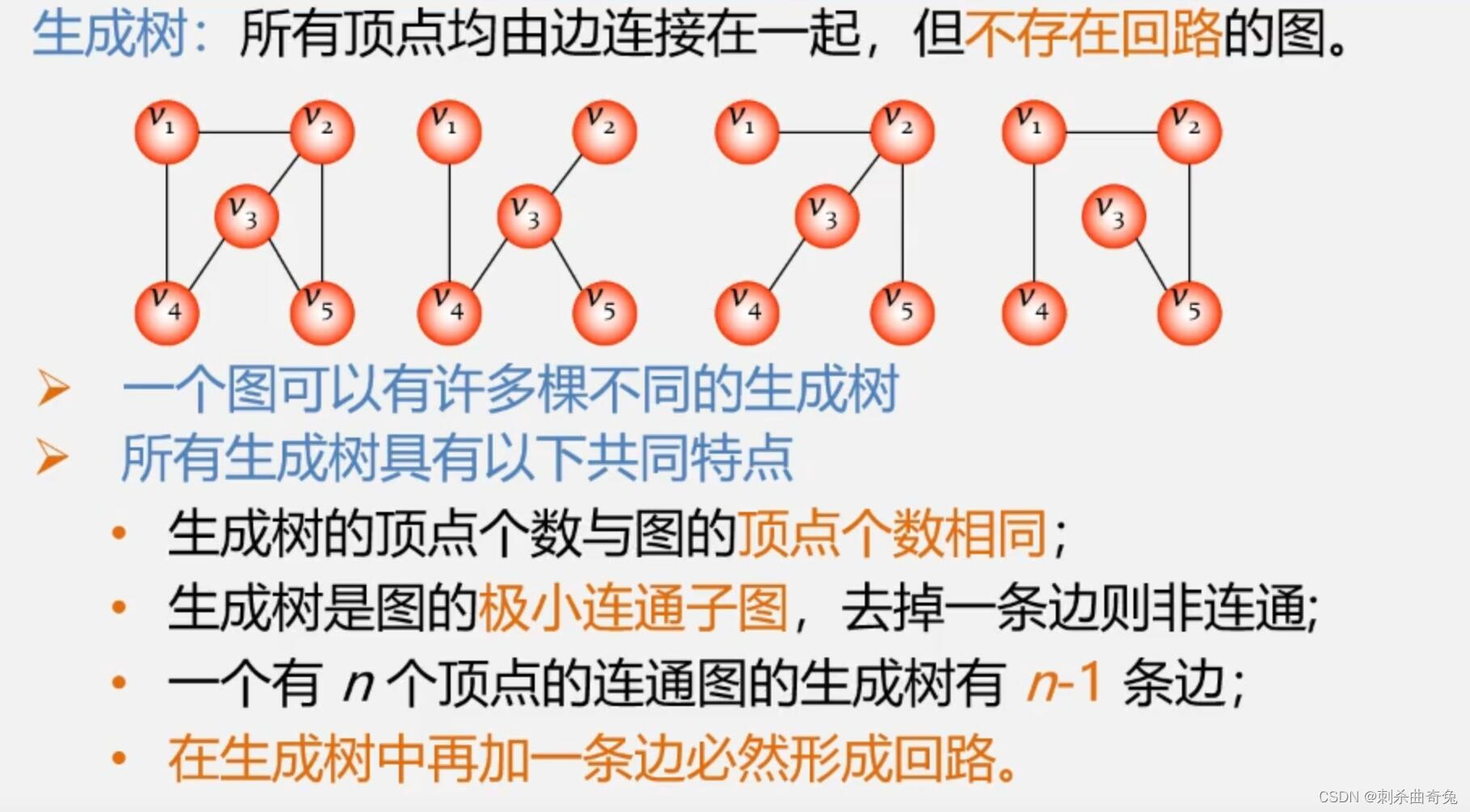
无向图的生成树
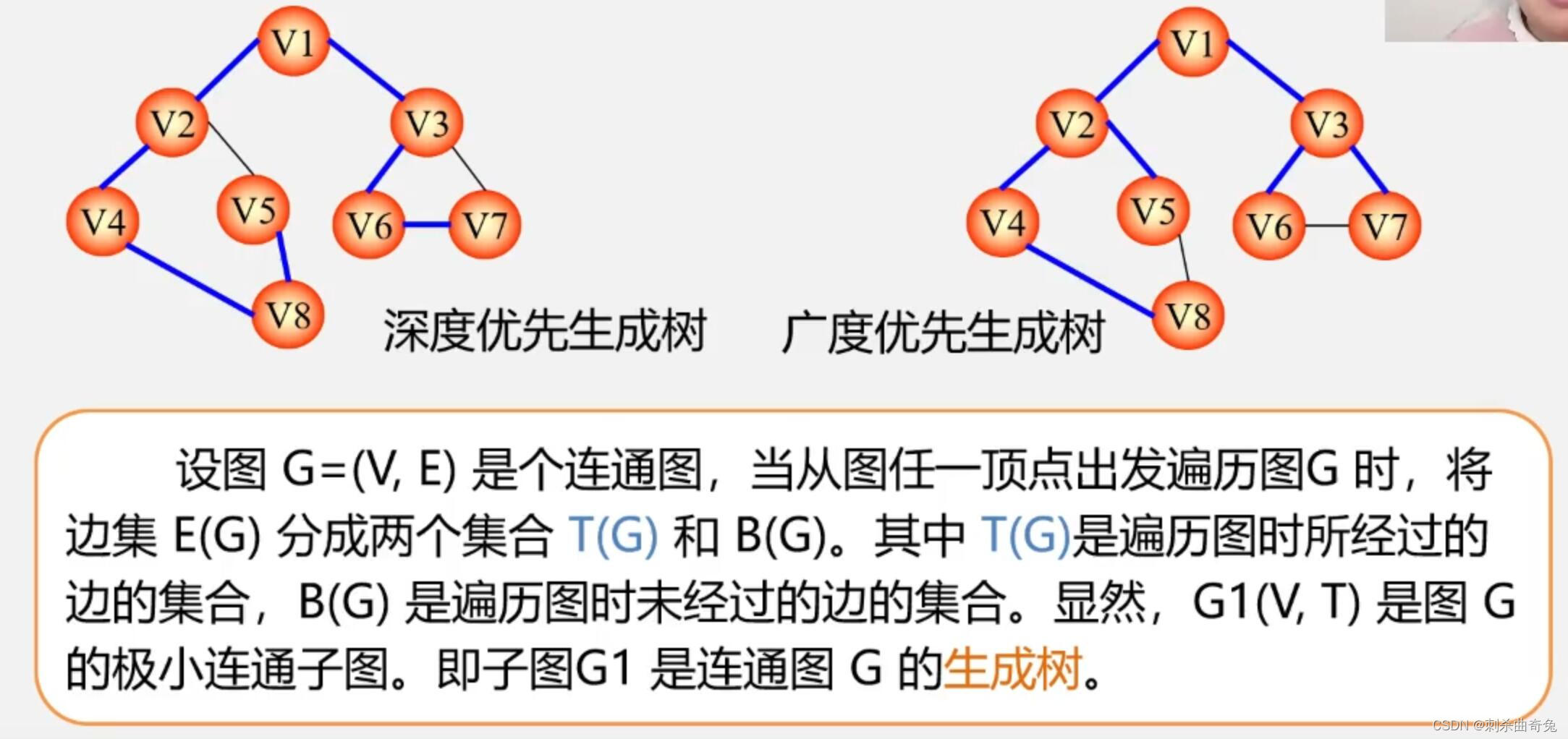
最小生成树
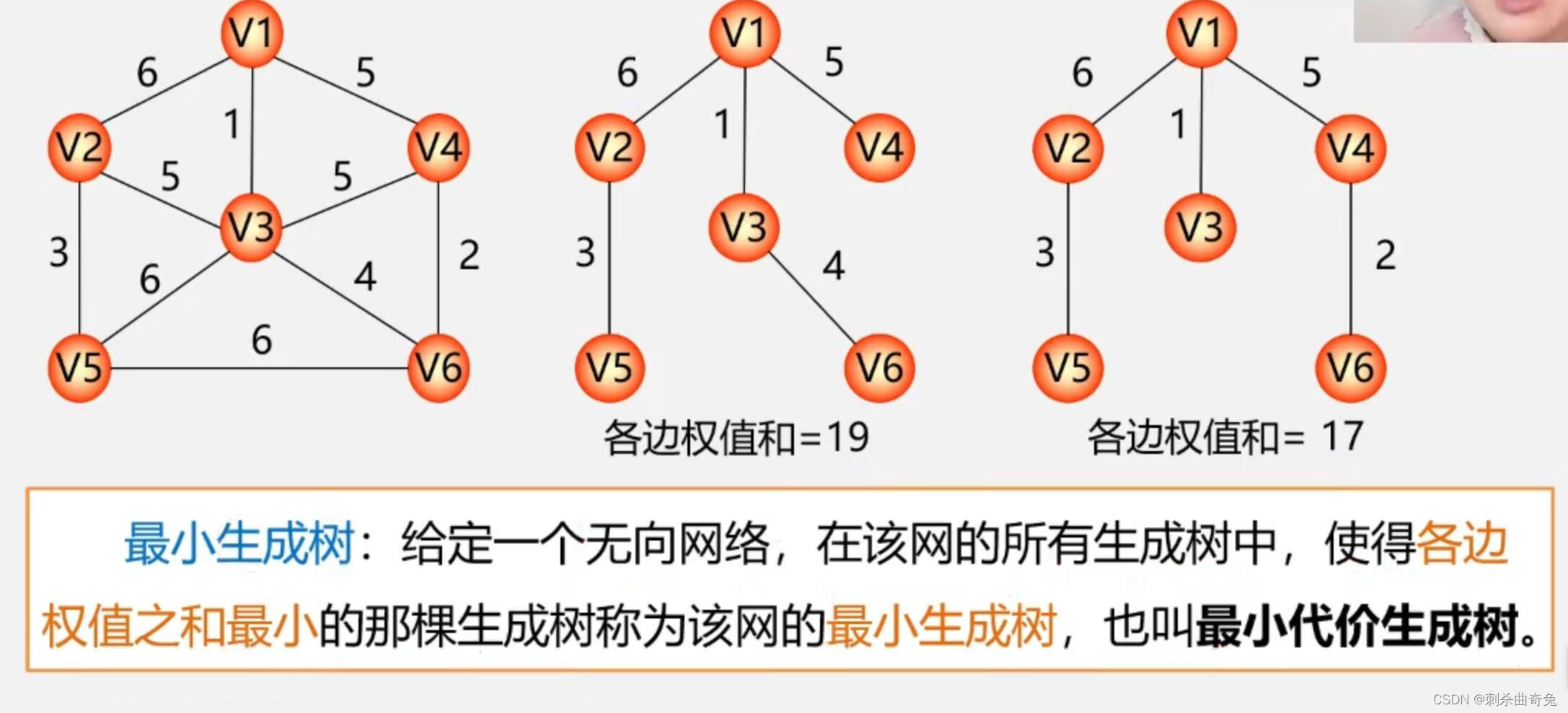
构造最小生成树
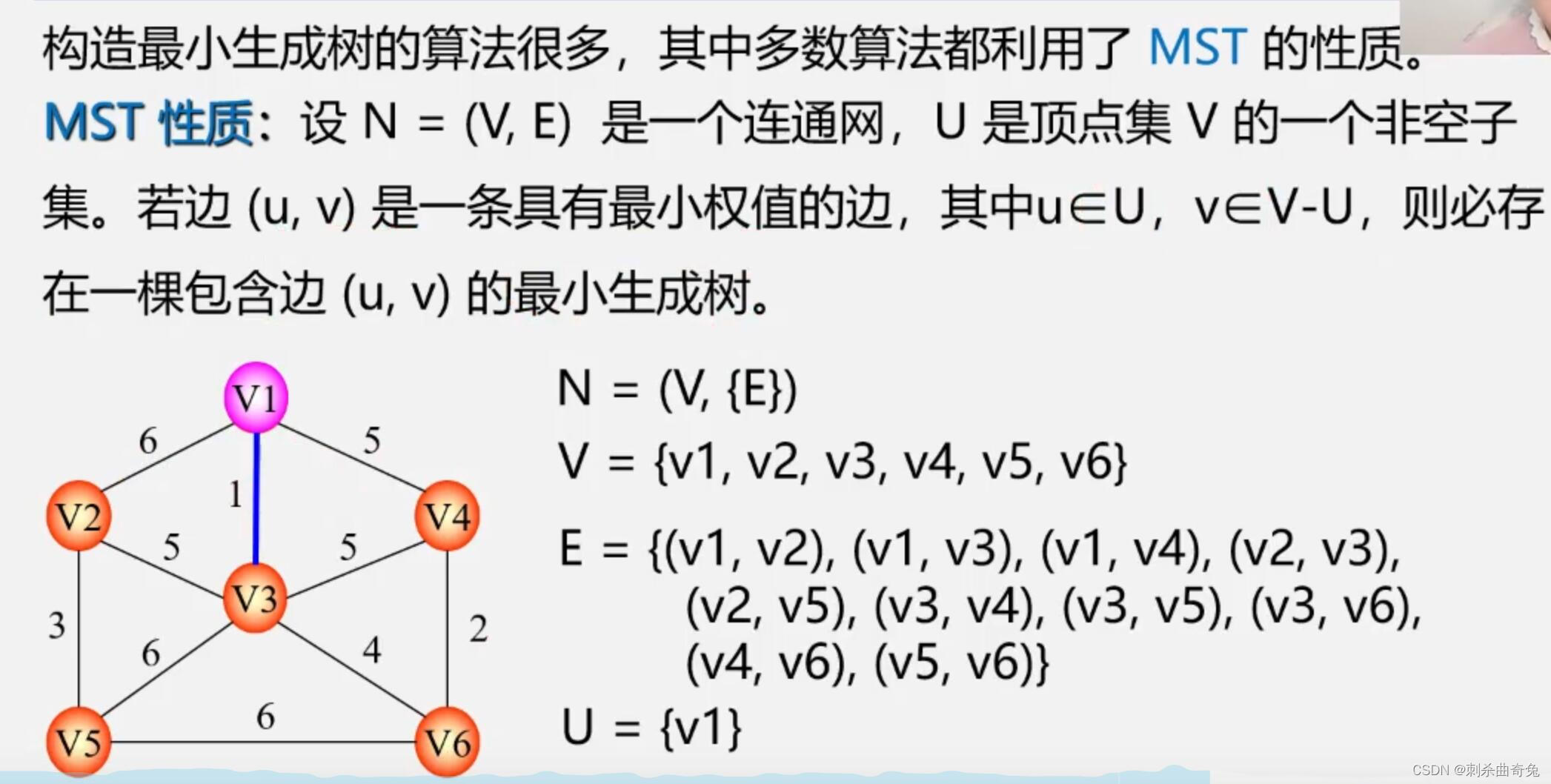
MST性质解释
在生成树的构造过程中,图中n个顶点分属两个集合:
已落在生成树上的顶点集:u
尚未落在生成树上的顶点集: V-U
接下来则应在所有连通U中顶点和V-U中顶点的边中选权值最小的边。
法一:普里姆算法
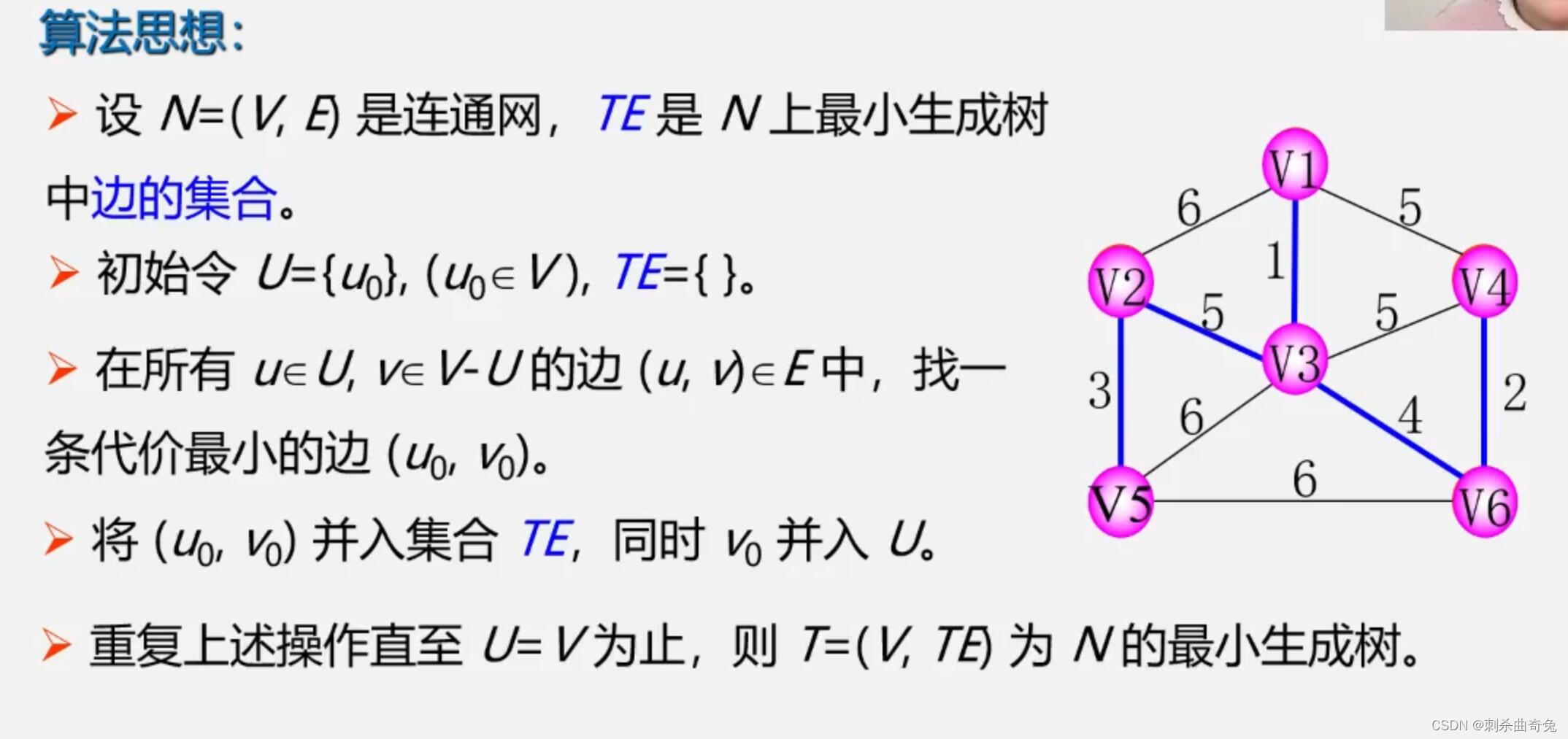
法二:克鲁斯卡尔算法

| 算法名 | 普里姆算法 | 克鲁斯卡尔算法 |
|---|---|---|
| 算法思想 | 选择点 | 选择边 |
| 时间复杂度 | O(n2)(n为顶点数) | o(eloge)(e为边数) |
| 适应范围 | 稠密图 | 稀疏图 |
最短路径
第一类问题:两点间最短路径
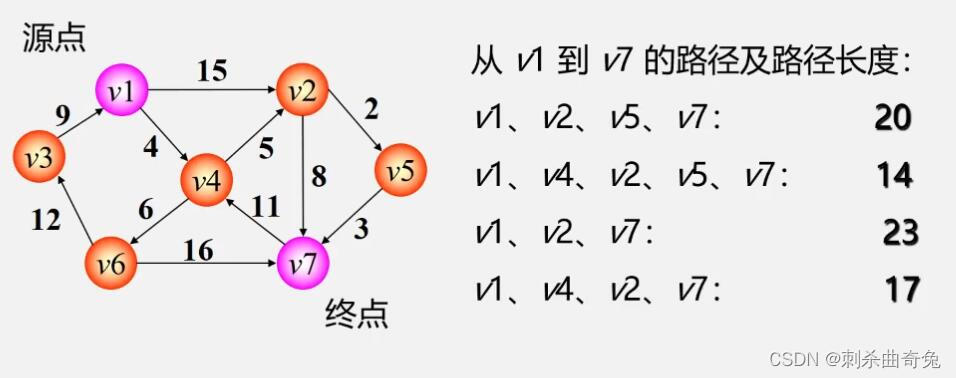
第二类问题:某源点到其他各点最短路径
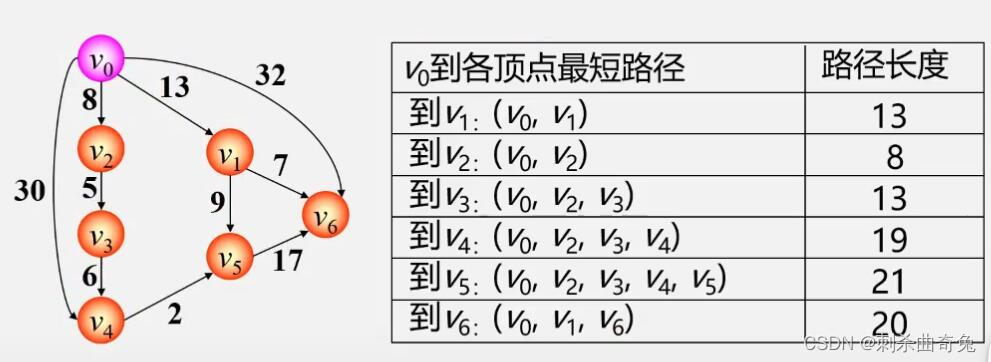
两种常见的最短路径问题:
一、单源最短路径—用Dijkstra(迪杰斯特拉)算法
二、所有顶点间的最短路径—用Floyd(弗洛伊德)算法
迪杰斯特拉(Dijistra)算法
1.初始化:先找出从源点vo到各终点v的直达路径(vorVk),即通过一条弧到达的路径。
2选择:从这些路径中找出一条长度最短的路径(vo,u)。
3.更新:然后对其余各条路径进行适当调整:
若在图中存在弧(u,vk),且(Vo,u) +(u,Vk)< (Vo,vk), 则以路径(Vo,u;Vk)代替(vo,Vk)。
在调整后的各条路径中,再找长度最短的路径,依此类推。
迪杰斯特拉(Dijistra)算法:按路径长度递增次序产生最短路径
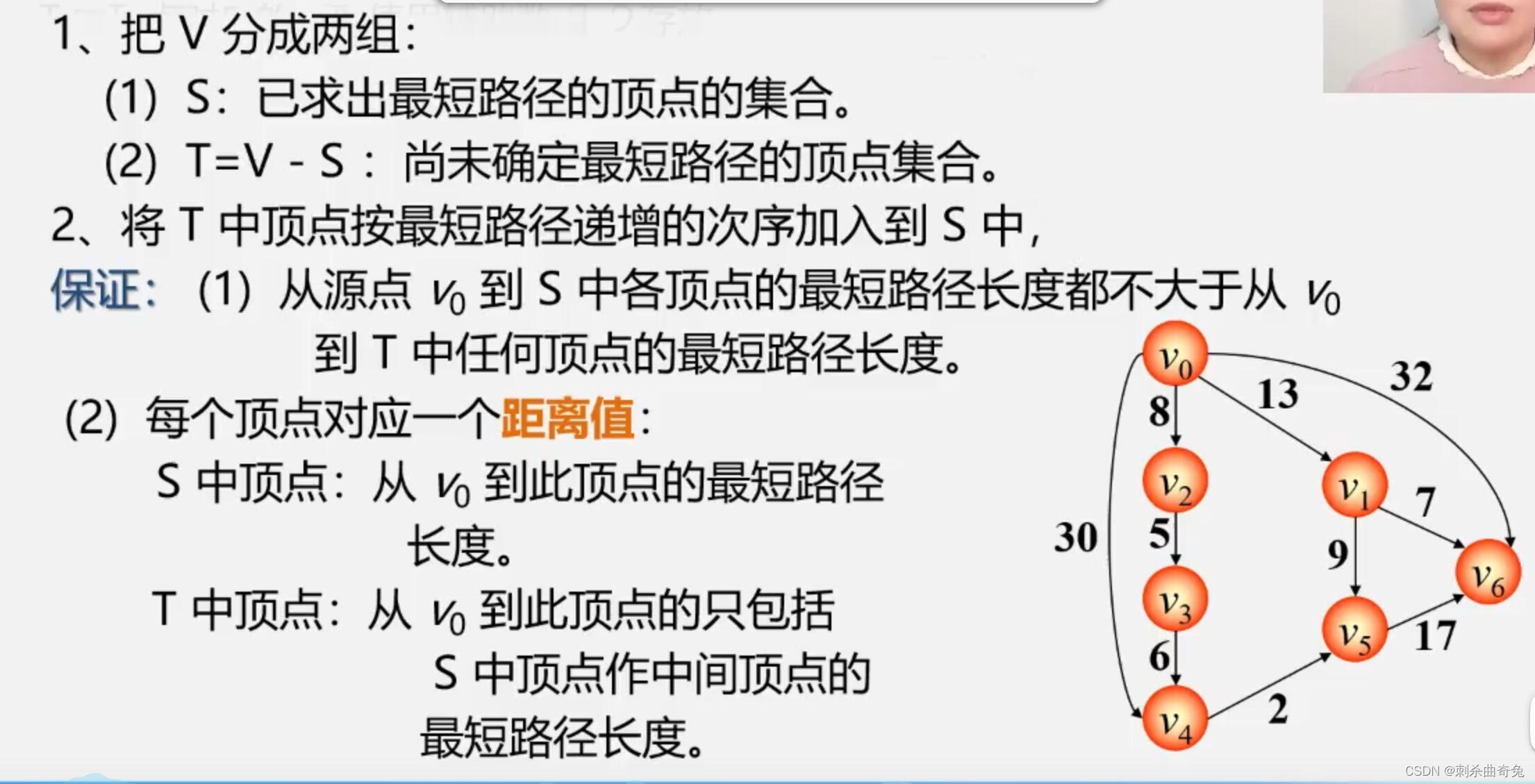
迪杰斯特拉(Dijistra)算法
 所有顶点间的最短路径
所有顶点间的最短路径
方法一:每次以一个顶点为源点,重复执行Dijikstra算法n次。
方法二:
弗洛伊德(Floyd)算法
算法思想:
逐个顶点试探
从vi,到vj的所有可能存在的路径中选出一条长度最短的路径
例:采用Floyd算法,求图中各顶点之间最短路径
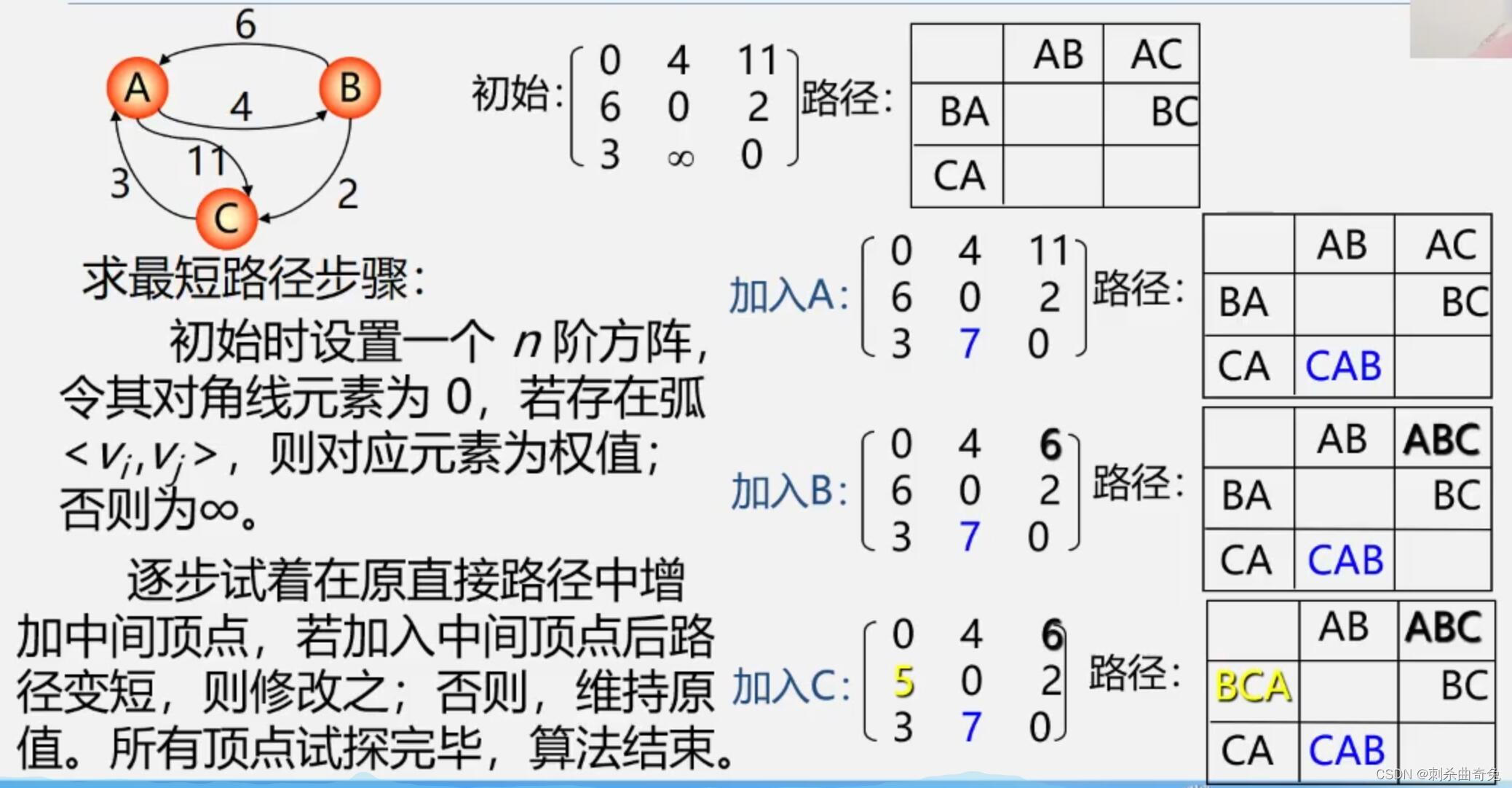
拓扑排序
有向无环图
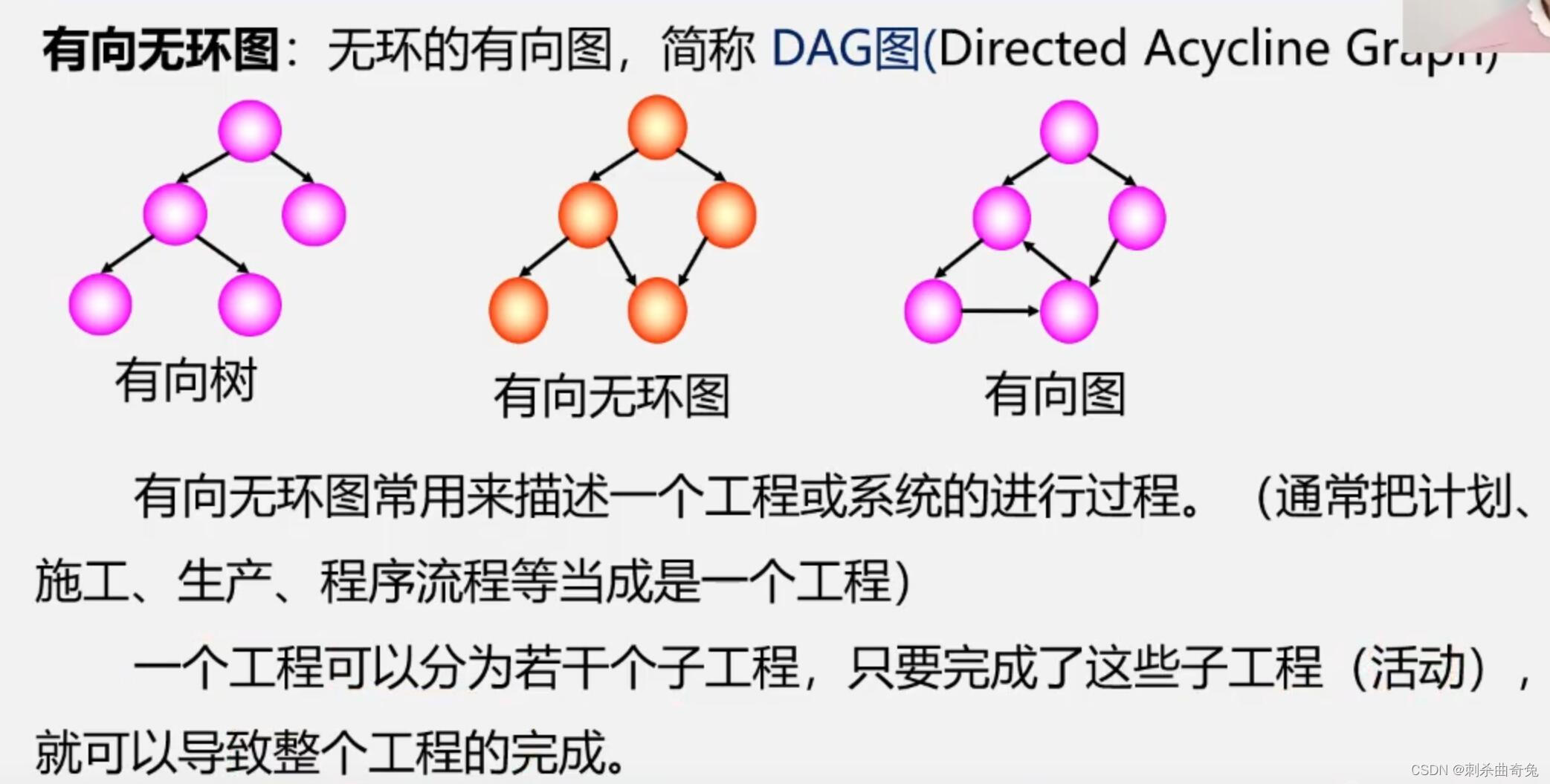
有向无环图及其应用

拓扑排序例:排课表
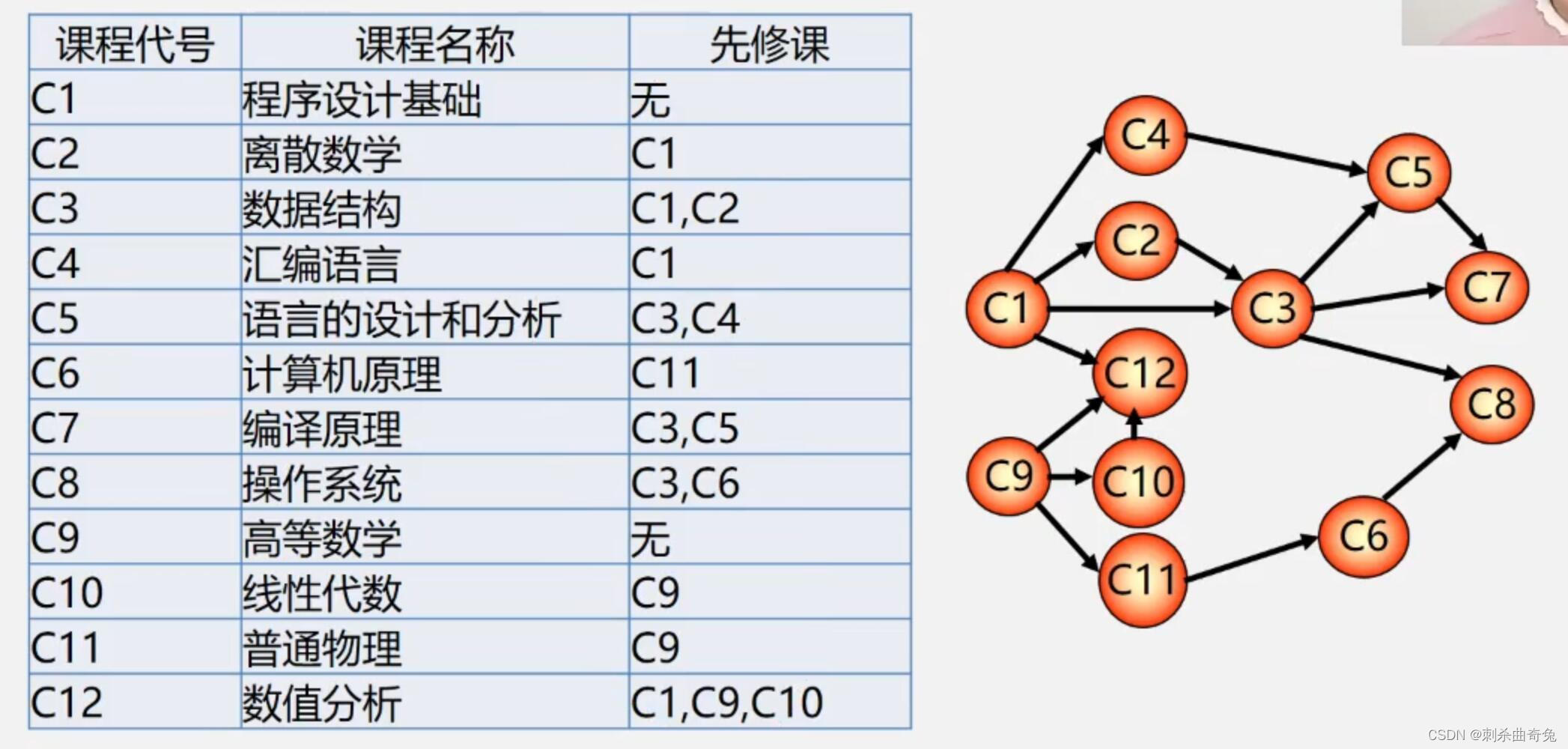
AOV网的特点:

问题:如何判别AOV网中是否存在回路?
拓扑排序:
在AOV网没有回路的前提下,我们将全部活动排列成一个线性序列,使得若AOV网中有弧<i, j>存在,则在这个序列中, i 一定排在 j 的前面,具有这种性质的线性序列称为拓扑有序序列,相应的拓扑有序排序的算法称为拓扑排序。
拓扑排序的方法:
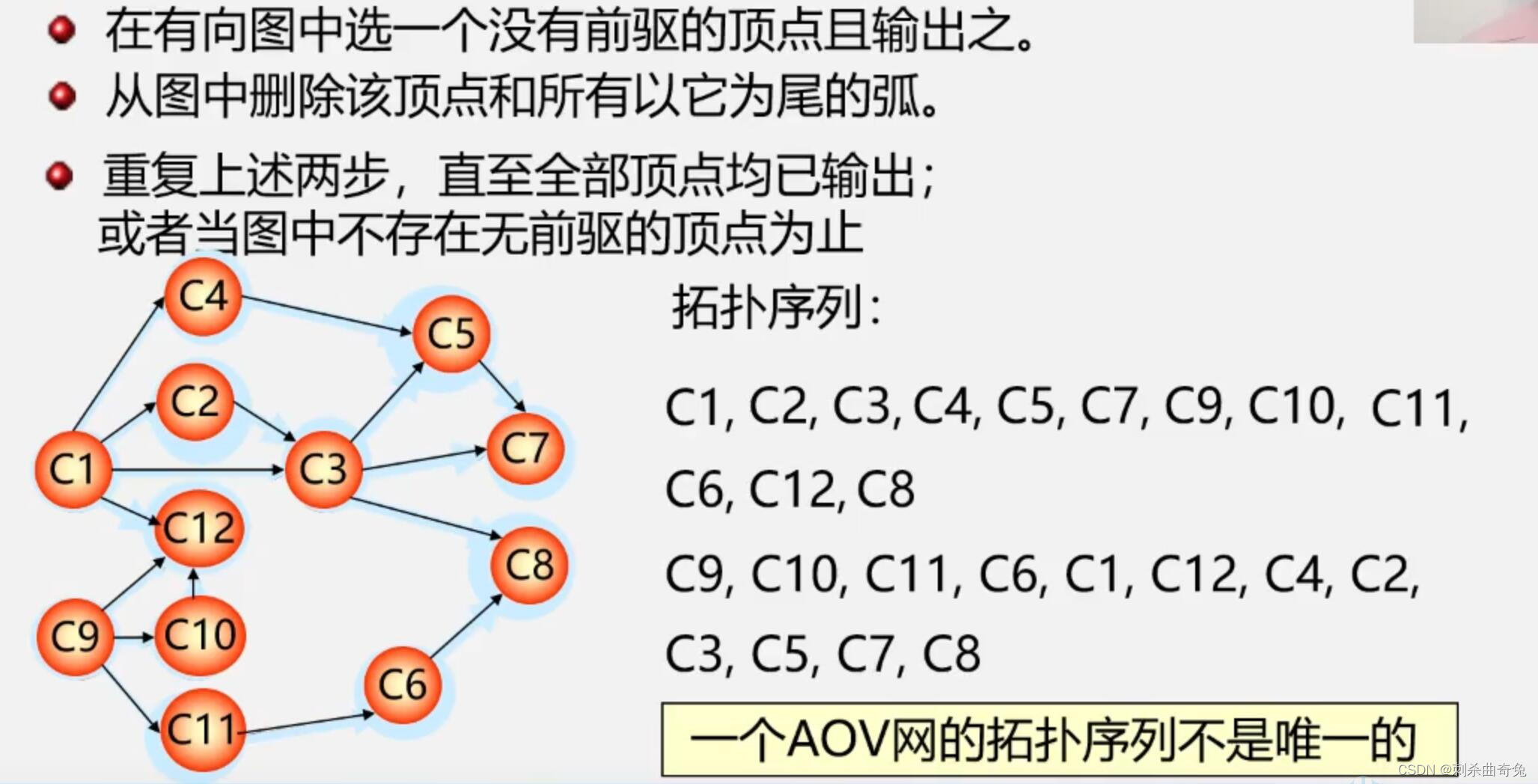
检测AOV网中是否存在环:
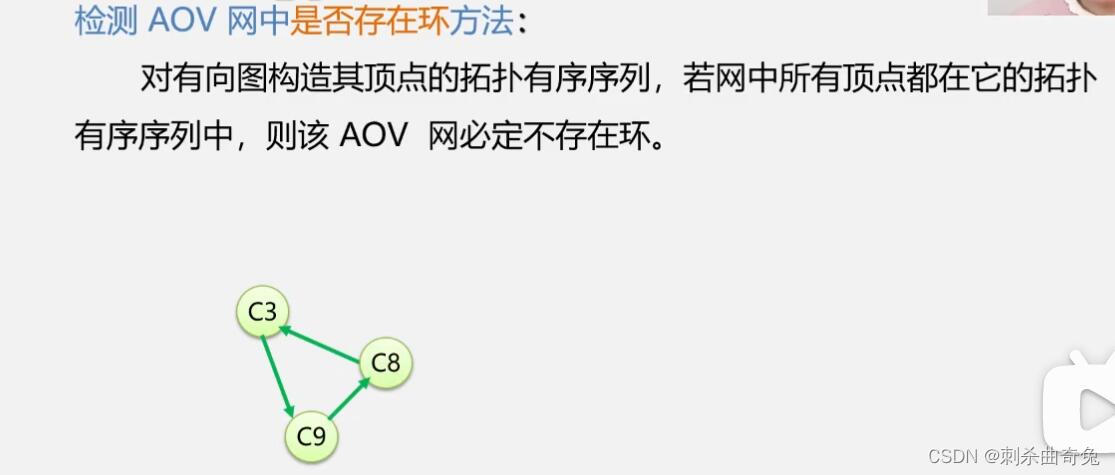
只剩下这个环时没有不存在前驱的结点,导致无法继续进行,序列结点与原总结点数不等,证明存在环
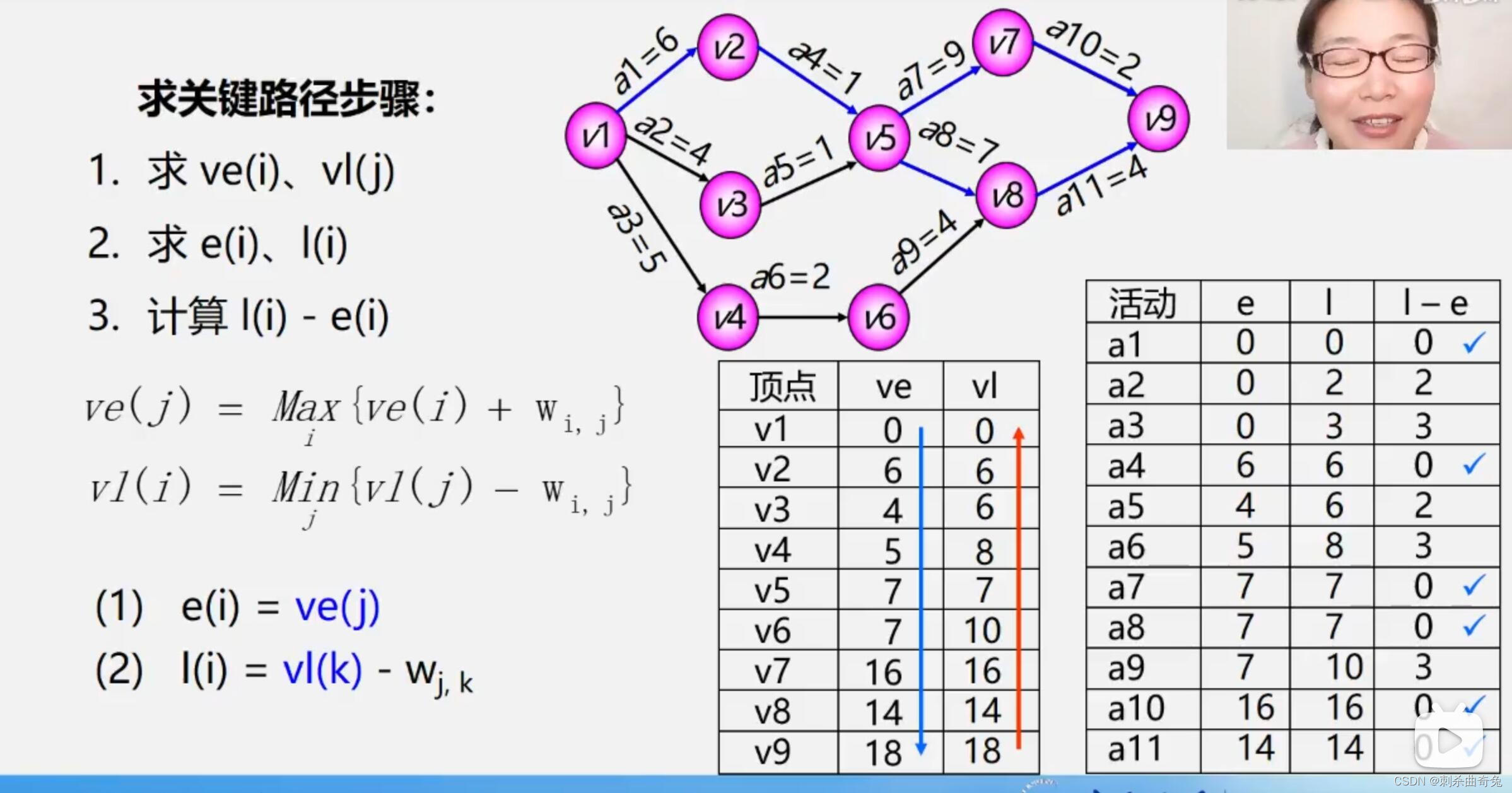
关键路径
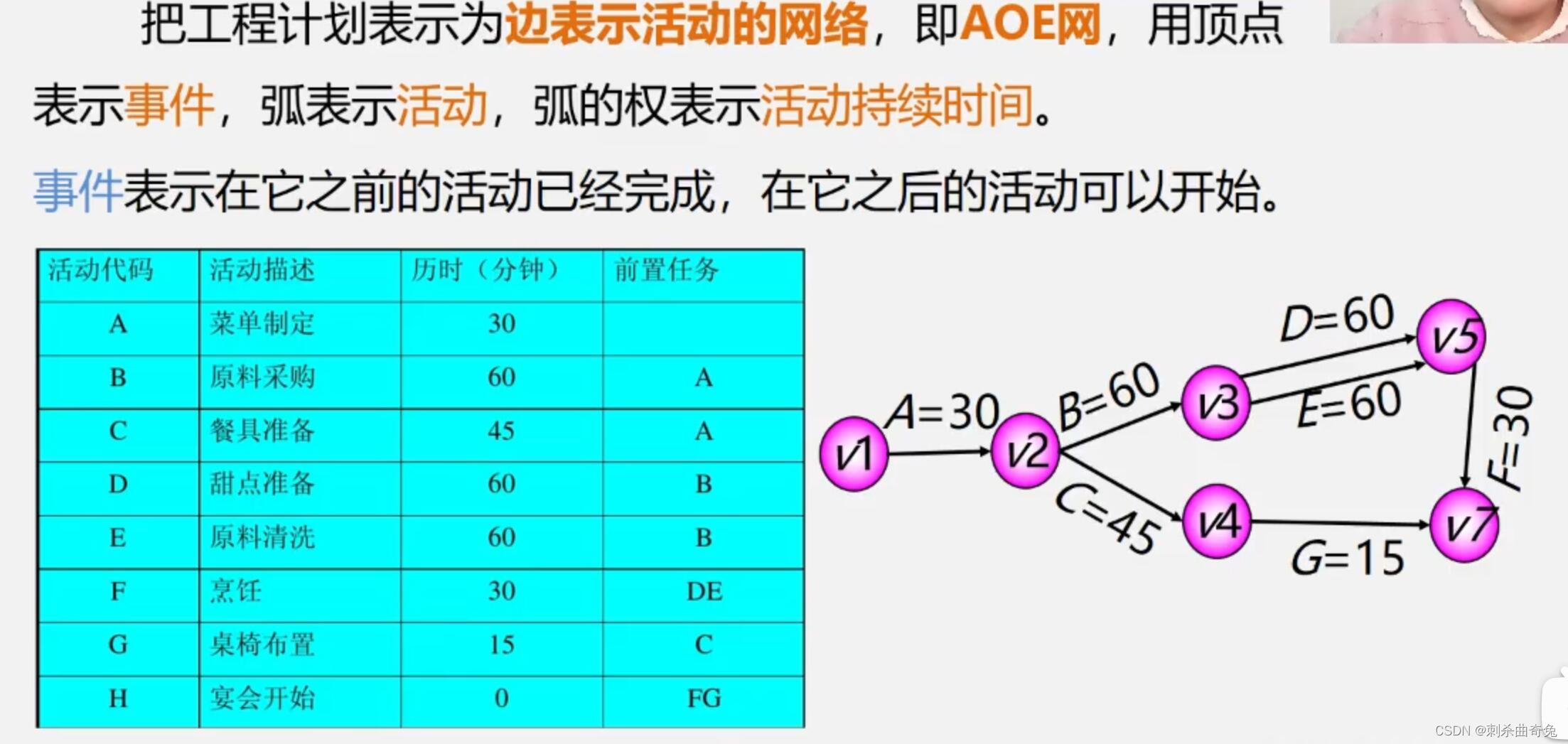
如何确定关键路径
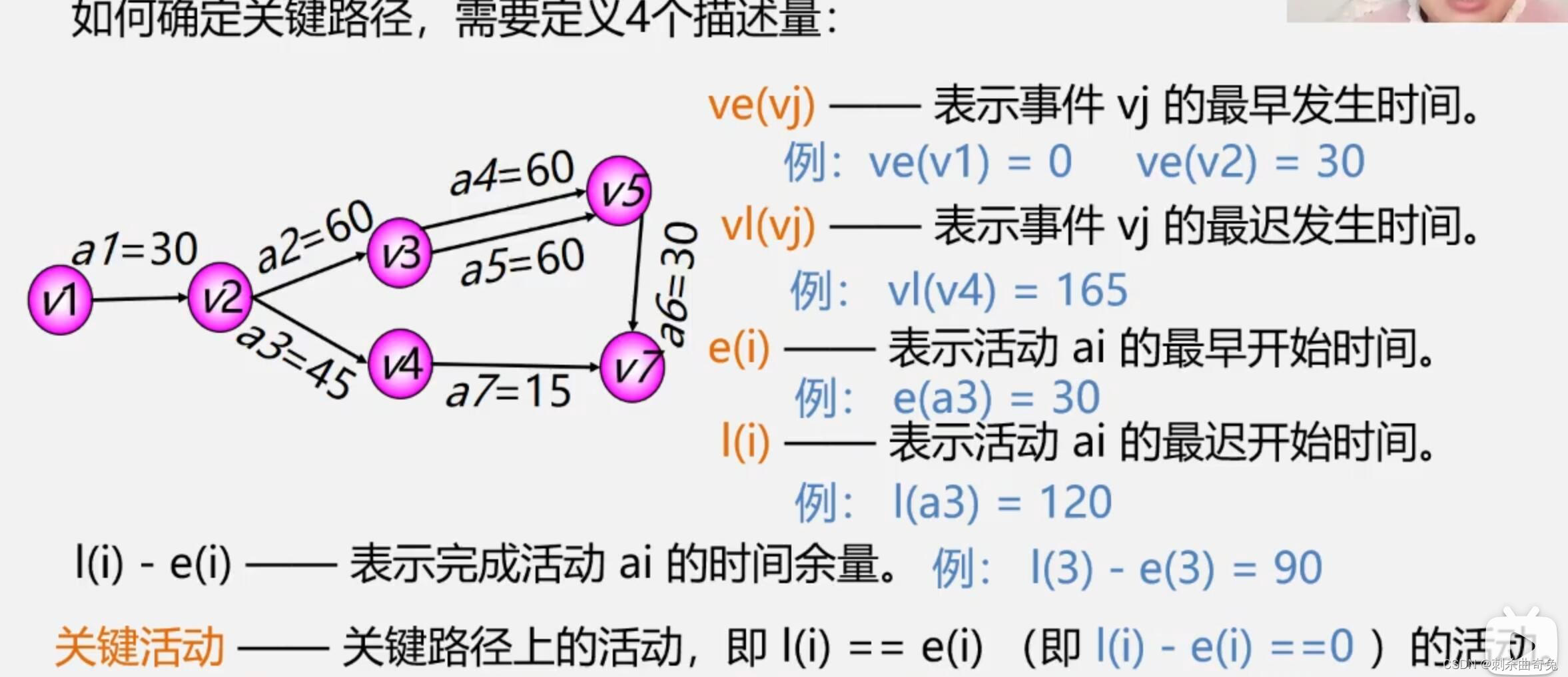
求关键路径步骤