工程电磁场仿真实验-用超松弛法求接地金属槽内电位分布
一、实验目的
1.熟悉利用超松弛法描绘出接地金属槽的电位分布情况;
2.学会使用MATLAB进行数值计算,并绘出相应的图形;
二、实验原理
1.有限差分法:
基本思想:将场域离散为许多网格 ,应用差分原理,将求解连续函数φ的微分方程问题转换为求解网格节点上φ的代数方程组的问题。
题目要求:
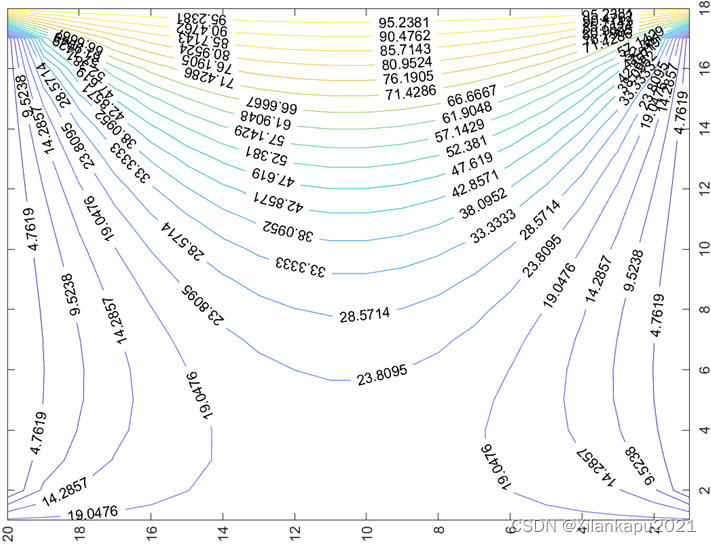
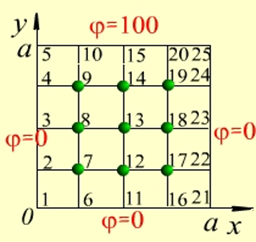
设有一个长直接地金属矩形槽( a = 20cm, b=18cm) , 如图所示, 其侧壁与底面电位均为0V, 顶盖电位为100V, 计算:迭代次数 N =?和电位分布。
具体要求:
(1)用matlab编写一个计算机程序。
(2)相邻两次迭代值的最大允许误差小于10-5。
(3)按正方形网格离散化场域,步长h = 1cm, 用有限差分法求槽内电位数值。
(如下图所示)
Matlab代码:
clear;%清除变量
for j=1:1:18%设置18mm长的纵坐标
a(1,j)=0;%左侧电位都为零
a(20,j)=0;%右侧电位都为零
end;%第一个for循环结束
for i=1:1:20%设置20mm长的横坐标
a(i,1)=0;%接地侧电位都为零
a(i,18)=100;%远地侧电位为零
end;%第二个for循环结束
w=1;%循环初步条件
n=0;%迭代次数
b=a;%将a的值赋予给b
while w >=0.00001;%设置两次迭代值的误差小于0.00001
w=0;%给w赋初值为0
for j=2:1:17;%纵坐标从2循环迭代到17(j=18上侧无数据无法进行迭代,且电位已知为100V;j=1同理电位已知为0V
for i=2:1:19;%横坐标从2循环迭代到19(i=0和i=20四周电位数据不够,不符合迭代条件且已知i=1电位为0V、i=20电位为0V
n=n+1,%记录迭代次数
temp=a(i,j);%将a(i,j)的值赋予给temp
a(i,j)=temp+1.72/4*(a(i+1,j)+a(i-1,j)+a(i,j+1)+a(i,j-1)-4*temp),%超松弛迭代法公式代码
if(abs(a(i,j)-temp)>w)%判断迭代循环条件
w=abs(a(i,j)-temp),%判断a(i,j)-temp的绝对值是否复合两次迭代值的误差
end;%if结构结束
end;%第二个for循环结束
end;%第一个for循环结束
end;%while语句结束
subplot(1,2,1),mesh(a) %将多个图画在1行2列的从左到右从上到下的第一个位置的同一平面上;指定a的三维网格图
axis([0,18,0,20,0,100])%设置下x,y,z坐标轴的限制范围
title('接地金属槽三维网格电位分布图')%添加标题
subplot(1,2,2),contour(a,20,'ShowText','on')%以20个等高线层绘制矩阵a的等高线图并注明等高线的数值
title('接地金属槽二维平面分布')%添加标题
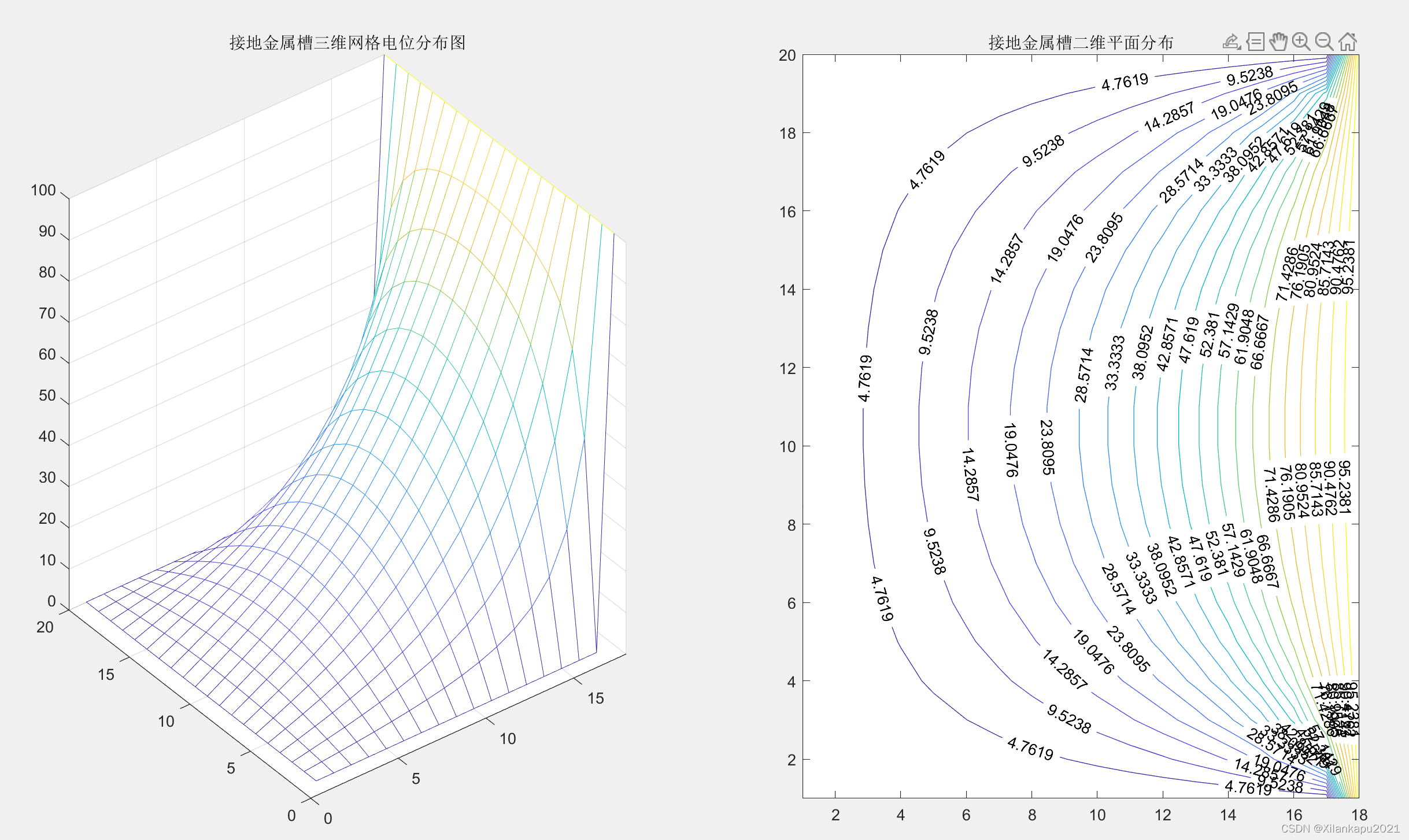
其中收敛因子a取值不同,对迭代次数有一定影响,如下表所示:
收敛因子(a) 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0
迭代次数(N) 93024 76896 63072 50688 39456 29088 16992 22752 46656 发散
表 1不同收敛因子对应的迭代次数
根据公式有 解得a的迭代值仍偏大,所以根据观察法初步判断最佳收敛因子在1.7-1.8之间。故通过实验法重复更改a的值有如下表:
收敛因子(a) 1.70 1.71 1.72 1.73 1.75
迭代次数(N) 16992 16128 16128 17280 19296
表 2缩小范围后的收敛因子与迭代次数关系表
因此,最后取最佳收敛因子a=1.72.
其中由于矩阵方程组谱半径小于1,则超松弛因子的的取值范围0<w<2是超松弛迭代法的必要条件。
松弛半径 0<w<1: 低松弛迭代法
松弛半径 w=1 : 高斯-赛德尔迭代法
松弛半径 1<w<2 :超松弛迭代法
当松弛因子w=2时,接地金属的电位图便发散,由于此时超松弛迭代法的计算结果已经无法收敛,所以两次迭代值的误差无法满足小于0.00001的精度要求。所以matlab会一直运行,不断迭代。所以发散的显示特征应该是没有输出图像。
各个离散点的电位值

附:特殊边界的接地金属的电位分布
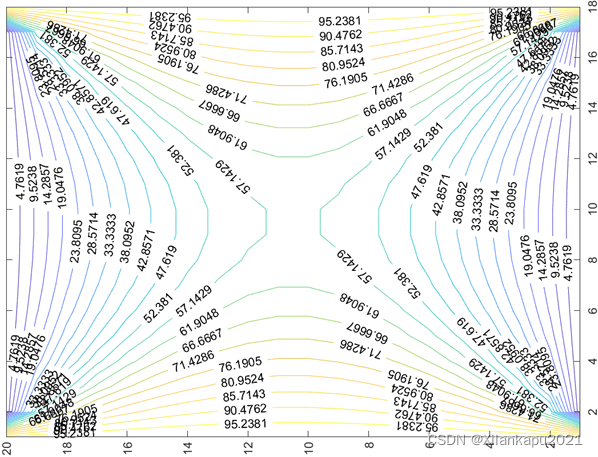
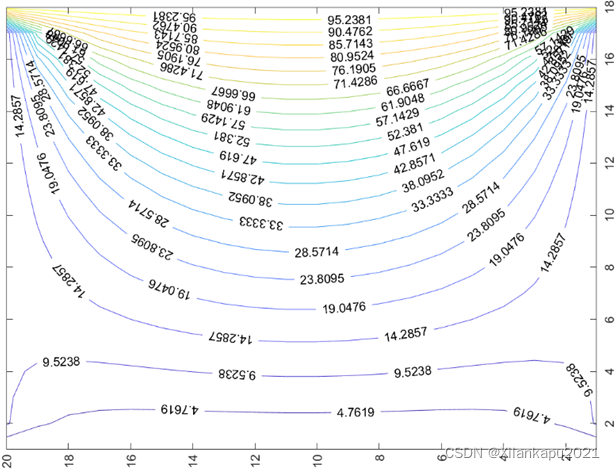
1.在工程电磁场用超松弛迭代求接地金属槽的电位分布时,其顶端的电位分布为100v(或为其他定值),而其余三侧的电位均为0V.当改变另外三侧的电位值不为0V时即可形成如下的电位分布图,便于理解三维分布图形式电位分布的含义。但下图展示二维电位分布图,若需了解掌握还请用matlab进行仿真。
二维电位分布图如下图所示: