?1 简介
经济快速发展背景下,物流配送活动成为大众生活中的关键部分.值得注意的是,由现代物流配送作业中看,强调多目标的实现,包括配送作业效率,客户满意度等,这就要求在配送线路上合理规划,并改进运输方式,这样在保证配送科学化的基础上,使配送效益提高.本次研究将对车辆路径优化问题做简单介绍,提出同时取送货车辆路径问题优化中的遗传算法应用,在此基础上做实证与仿真分析.





2 部分代码
%主函数
%基于遗传算法求解同时取送货的车辆路径问题
tic;
clc;
clear?all
close?all;
global?CARLOAD;
global?Popsize?Num;
global?Delivery?Pickup?Dis_MATRIX;
global?Pc?Pm;
global?genmax;
Pc=0.85;?%交叉概率
Pm=0.01;?%变异概率
CARLOAD=100;?%车辆最大载重
Popsize=100;?%种群规模
Num=100;?%调配点个数
genmax=200;?%最大迭代代数
data=xlsread('data.xlsx');
data=data(1:Num+1,:);
%计算各节点间的直线距离
Dis_MATRIX=ones(Num+1);
for?i=1:Num+1
? ?for?j=1:Num+1
? ? ? ?Dis_MATRIX(i,j)=sqrt((data(i,2)-data(j,2))^2+(data(i,3)-data(j,3))^2);
? ?end
end
vertexs=data(:,2:3);
Delivery=data(2:end,4);
Pickup=data(2:end,5);
chrom=[];
for?i=1:Popsize
? ?chrom(i,:)=randperm(Num);?%初始化种群
end
counter=1;
while?counter<=genmax
y=bestfit;
%找出最优的适应值、个体
[maxbestfit,maxindex]=max(bestfit);%取最优适应值的位置、最优适应值
maxindex=maxindex(1);
maxbestpop=bestpop(maxindex,:);%取最优个体
[R,Rlength,carNum]=OUTPUT(maxbestpop);?%最优路径
%迭代图
figure
x=1:1:genmax;
plot(x,y);
title('优化过程');
xlabel('迭代次数');
ylabel('最优适应值');
disp(['最优路径为:',num2str(R)]);
disp(['最短长度为:',num2str(Rlength)]);
disp(['车辆数为:',num2str(carNum)]);
%% 打印全局最优解路线图
j=1;
R=R;
RR=[];
for?i=2:length(R)
? ?
? ?if?R(i)==0
? ? ? ?VC{j}=RR;
? ? ? ?j=j+1;
? ? ? ?RR=[];
% ? ? ? ? RR=[RR R(i)];
? ?else
? ? ? ?
? ? ? ?RR=[RR?R(i)];
? ? ? ?
? ?end
end
draw_Best(VC,vertexs);
toc;
3 仿真结果

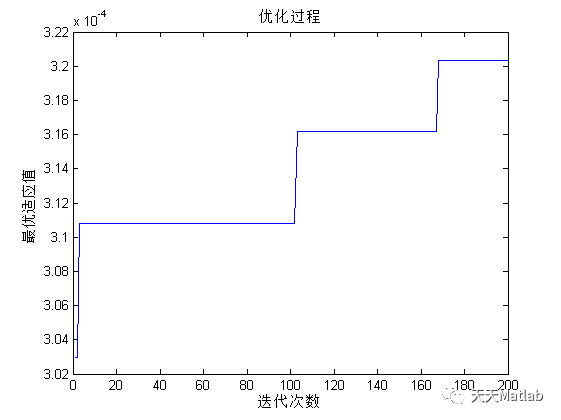
4 参考文献
[1]汤浩晨. "基于遗传算法的同时取送货车辆路径问题优化模型及算法研究." (2018).
部分理论引用网络文献,若有侵权联系博主删除。
