开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【一起啃西瓜书】机器学习-期末复习（不挂科） -> 正文阅读

[数据结构与算法]【一起啃西瓜书】机器学习-期末复习（不挂科）

【一起啃西瓜书】机器学习-期末复习（不挂科）

前言
试卷题型
第一章：绪论
- 一般过程
- 任务
- 数据
- 训练集
- 验证集
- 监督学习
- 无监督学习
- 半监督学习
第二章：模型评估与选择
- 欠拟合与过拟合
- 评估方法
- 性能度量
- - 错误率&精度
  - 查准率&查全率
- 交叉验证
第三章：线性模型
- 线性回归&分类
- 基本形式
- 线性模型优点
- 参数/模型估计
- 对数线性回归
- 对数几率回归
- 多分类学习
- - 一对其余
  - 两种策略比较
- 类别不平衡
- 优化提要
- 线性回归
- 波士顿房价预测
- 癌细胞预测
- - - 梯度下降
    - 逻辑回归api介绍
- 手写数字识别
第四章：决策树
- 基本流程
- 划分选择
- 剪枝处理
- - 预剪枝
  - 后剪枝
- ID3，C4.5和CART算法对比
第五章神经网络
- 试推导出BP算法中的更新公式
- Some note for comprehend
第六章：支持向量机
- 什么是支持向量机
- 试析SVM 对噪声敏感的原因
- 核函数的作用
- 正则化
第七章：贝叶斯分类器
第八章：集成学习
- Boosting&Bagging
第九章：聚类
- 聚类任务
第十章：降维与度量学习
- 降维
总结

前言

马上西瓜书期末考试，为了不挂科，需要有针对复习，内容来自专业各个学霸及老师的重点划分。

推荐:【一起啃西瓜书】机器学习总览

试卷题型

卷面共100分，含5种题型，考试时间120分钟。

判断题，8道,每题2分，共16分;
填空题，7道,每题2分，共14分;
简答题，5道,每题4分，共20分;
演算题，2道，每题10分，共20分;
编程题，2道，一道编程填空题（10分），一道编程题（20分)，共30分。

第一章：绪论

在这里插入图片描述
机器学习致力于研究如何通过计算的手段，利用经验来改善系统自身的性能，从而在计算机上从数据（经验）中产生“模型”，用于对新的情况给出判断（利用此模型预测未来的一种方法）。

分为三类：监督学习、无监督学习、强化学习。

一般过程

数据获取
特征工程
模型选择
模型训练
模型评估
超参数条件
预测

更详细：

机器学习过程中,通过确定两方面的参数来找到泛化性能最好的函数:

函数参数,也就是我们通常所说的w和b，这类参数可以通过各种最优化算法自动求得;
模型参数,比如多项式回归中的多项式次数,规则化参数入等(即超参数)，一般在模型训练之前通过手工指定（当然也可以采用网格法等算法进行寻优)。

确定模型超参数的过程称为模型选择(从Algorithm选择Models)。

机器学习的一般过程:

确定模型的一组超参数，
用训练集训练该模型,找到使损失函数最小的最优函数,
在验证集上对最优函数的性能进行度量，
重复1、2、3步，直到搜索完指定的超参数组合，
选择在验证集上误差最小的模型,并合并训练集和验证集作为整体训练模型，找到最优函数,
在测试集上对最优函数的泛化性能进行度量。

任务

分类:离散值
回归:连续值
聚类:无标记信息

有无标记信息

监督学习：分类、回归
无监督学习：聚类
半监督学习：两者结合

数据

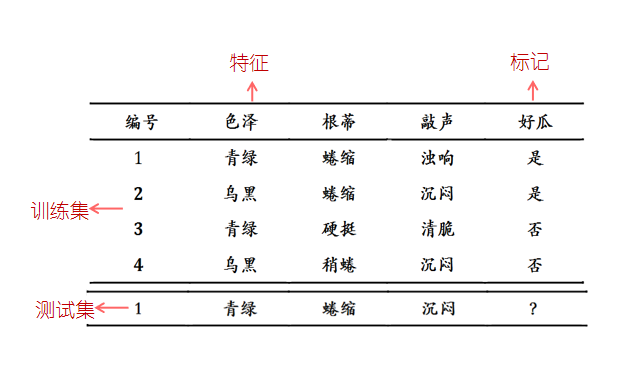
在这里插入图片描述

训练集

用于模型拟合的数据样本

验证集

在模型训练过程中单独留出来的样本集，它可以用于调整模型的超参数和用于对模型的初步评估。通常用来在模型迭代训练时，用以验证当前模型的泛化能力，但不能作为调参，选择特征等算法相关的选择的依据。

监督学习

定义：

输入数据是由输入特征值和目标值所组成。
函数的输出可以是一个连续的值(称为回归），或是输出是有限个离散值（称作分类）。

用已知某种或某些特征的样本作为训练集，以建立一个数学模型，再用已建立的模型来预测未知的样本的方法.是从标签化训练集数据集中推断出模型的机器学习任务.

无监督学习

定义：

输入数据是由输入特征值组成，没有目标值
- 输入数据没有被标记，也没有确定的结果。样本数据类别未知；
- 需要根据样本间的相似性对样本集进行类别划分

在算法构建过程中不考虑标签值，只通过特征信息去归纳一些新的规律出来.

半监督学习

定义：训练集同时包含有标记样本数据和未标记样本数据。

用少量有标注的样本和大量为标注的样本进行训练分类

第二章：模型评估与选择

欠拟合与过拟合

拟合：就是说这个曲线能不能很好的描述某些样本，并且有较强的泛化能力.

过拟合（训练集误差小，测试集误差大）
学习器把训练样本学习的“太好”，将训练样本本身的特点当做所有样本的一般性质（不考虑数据噪声），导致泛化性能下降
欠拟合（训练集误差大）
对训练样本的一般性质尚未学好

如何判断区分二者？

过拟合：模型过于复杂，导致训练误差低，测试误差高
欠拟合：模型简单，训练测试误差均高

解决：

过拟合

增加训练样本数量
正则化L1.L2
降维
集成学习方法
减少模型复杂度
丢弃法Dropout

欠拟合：

添加新特性
增加模型复杂度
减小正则化系数

决策树:拓展分支
神经网络:增加训练轮数

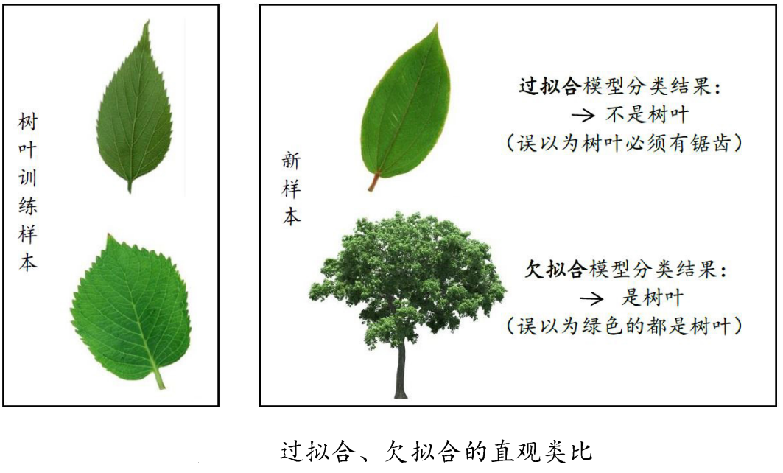
在这里插入图片描述

过拟合：学习器把训练样本本身特点当做所有潜在样本都会具有的一般性质.
欠拟合：训练样本的一般性质尚未被学习器学好.

评估方法

现实任务中往往会对学习器的泛化性能、时间开销、存储开销、可解释性等方面的因素进行评估并做出选择。

我们假设测试集是从样本真实分布中独立采样获得，将测试集上的“测试误差”作为泛化误差的近似，所以测试集要和训练集中的样本尽量互斥。

留出法：

直接将数据集划分为两个互斥集合
训练/测试集划分要尽可能保持数据分布的一致性
一般若干次随机划分、重复实验取平均值
训练/测试样本比例通常为2:1~4:1

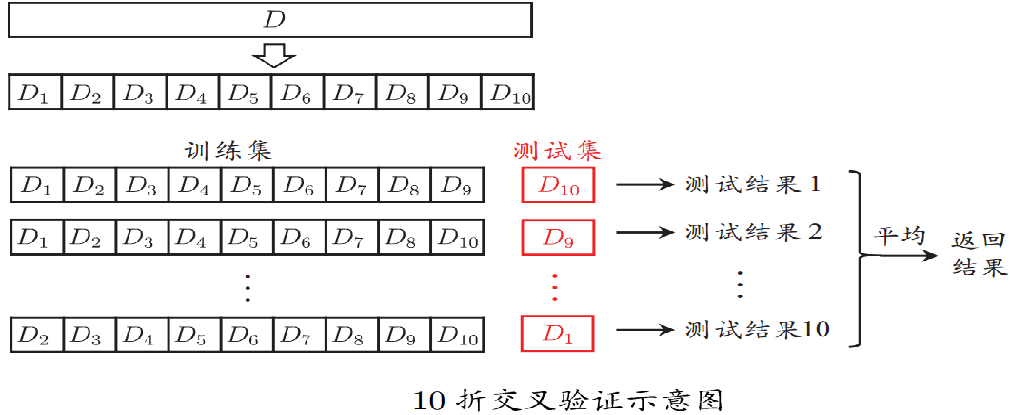
交叉验证法：

将数据集分层采样划分为k个大小相似的互斥子集，每次用k-1个子集的并集作为训练集，余下的一个子集作为测试集，最终返回k个测试结果的均值，k最常用的取值是10.

在这里插入图片描述
自助法：

以自助采样法为基础，对数据集D有放回采样m次得到训练集D’ , D\D’用做测试集。

实际模型与预期模型都使用m个训练样本
约有1/3的样本没在训练集中出现
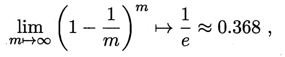
从初始数据集中产生多个不同的训练集，对集成学习有很大的好处
自助法在数据集较小、难以有效划分训练/测试集时很有用；由于改变了数据集分布可能引入估计偏差，在数据量足够时，留出法和交叉验证法更常用。

性能度量

性能度量是衡量模型泛化能力的评价标准，反映了任务需求；使用不同的性能度量往往会导致不同的评判结果

回归任务最常用的性能度量是“均方误差”：
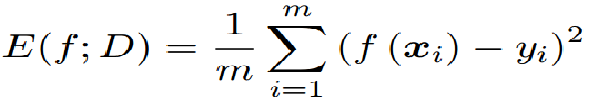
在这里插入图片描述

错误率&精度

对于分类任务,错误率和精度是最常用的两种性能度量：

错误率：分错样本占样本总数的比率
精度（正确率）：分对样本占样本总数的比率

查准率&查全率

信息检索、Web搜索等场景中经常需要衡量正例被预测出来的比率或者预测出来的正例中正确的比率，此时查准率和查全率比错误率和精度更适合。

统计真实标记和预测结果的组合可以得到“混淆矩阵”：

在这里插入图片描述
查准率：在预测结果中，预测正例对了所占所有预测正例中的比例（竖着来）

查全率：在真实情况中，预测正例对了所占所有真实情况中的比例（横着来）

在预测癌症患者时，优先考虑查全率，因为如果有一个人漏判了便很严重，所以我们更看重：真实患有癌症的情况下，模型预测正确的概率。

基于混淆矩阵，解释什么是TPR（True Positive Rate）真正利率，FPR（False Positive Rate）假正例率，查准率（P），查全率（R）？

TPR和R相等，都是真实正例被预测正确的比例，即：TPR=R=TP/TP+FN
FPR：真实反例被预测为正例的比率，即：FPR=FP/FP+TN
P：预测为正例的实例中，真正正例的比例，即：P=TP/TP+FP

在测试集上对最优函数的泛华性能进行度量.

交叉验证

为什么用交叉验证法？

交叉验证用于评估模型的预测性能，尤其是训练好的模型在新数据上的表现，可以在一定程度上减小过拟合
还可以从有限的数据中获取尽可能多的有效信息

第三章：线性模型

线性回归&分类

线性回归：试图学得一个线性模型以尽可能准确的预测实值输出标记
分类：即最常见的是二分类，在线性回归得出预测值之后，增加了一个“单位越界函数”

回归和分类的区别：

本质都是一致的，就是模型的拟合（匹配），但是分类问题的y值（label）更离散化一些.而且同一个y值可能对应一大批的x，这些x是具有范围的。所以分类问题更多的是（一定区域的X）对应着一个y标签。而回归问题的模型更倾向于（很小区域内的X或者一般是一个X）对应着一个y.

基本形式

线性模型一般形式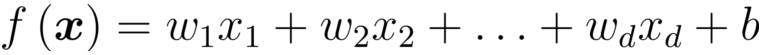： 在这里插入图片描述
$x$ ：属性描述的示例， $x i$ ：是 $x$ 在第 $i$ 个属性上的取值.

向量形式：

$f(x) = w^Tx + b$

$w = (w_1;w_2;...;w_d)$ ：向量表示

线性模型优点

形式简单、易于建模
可解释性
非线性模型的基础
- 引入层级结构或高维映射

线性回归（linear regression）目的

学得一个线性模型以尽可能准确地预测实值输出标记

单一属性的线性回归目标：

$f(x) = w^Tx + b$

参数/模型估计

参数/模型估计：最小二乘法（least square method）

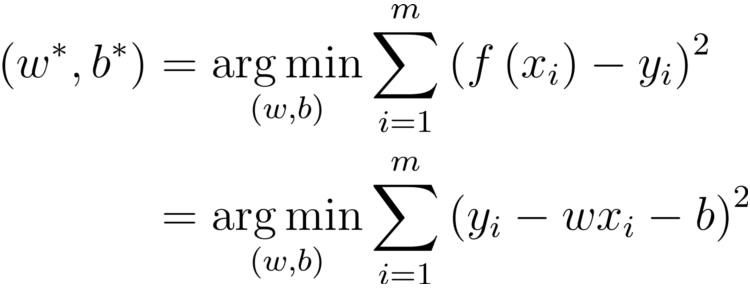
在这里插入图片描述
最小化均方误差

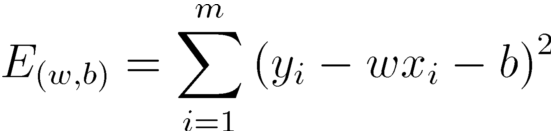
在这里插入图片描述
分别对 $w$ 和 $b$ 求导，可得：

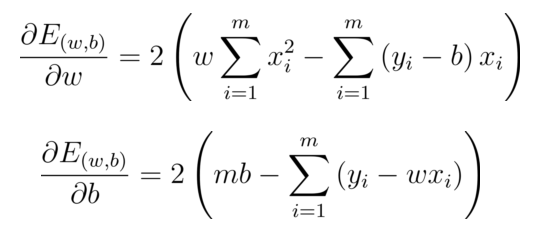
在这里插入图片描述
基于均方误差最小化来进行模型求解的方法为最小二乘法.

在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

对数线性回归

输出标记的对数为线性模型逼近的目标:

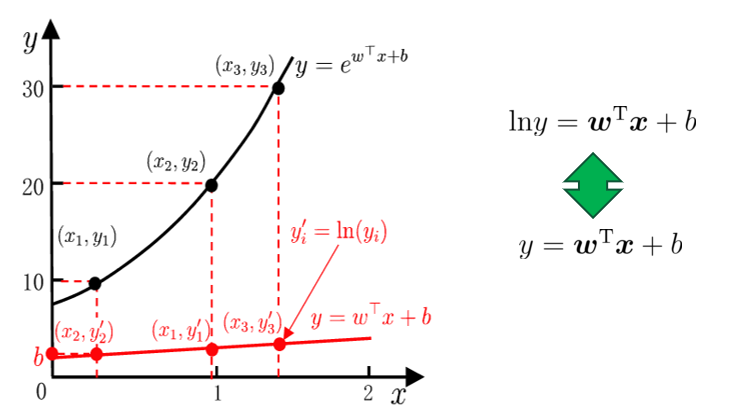
在这里插入图片描述

对数几率回归

二分类任务

$z = w^Tx + b$

寻找函数将分类标记与线性回归模型输出联系起来:

最理想的函数——单位阶跃函数
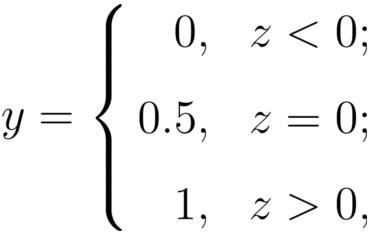
在这里插入图片描述

预测值大于零就判为正例，小于零就判为反例，预测值为临界值零则可任意判别

单位阶跃函数缺点：不连续

替代函数——对数几率函数（logistic function）

单调可微、任意阶可导

单位阶跃函数与对数几率函数的比较：
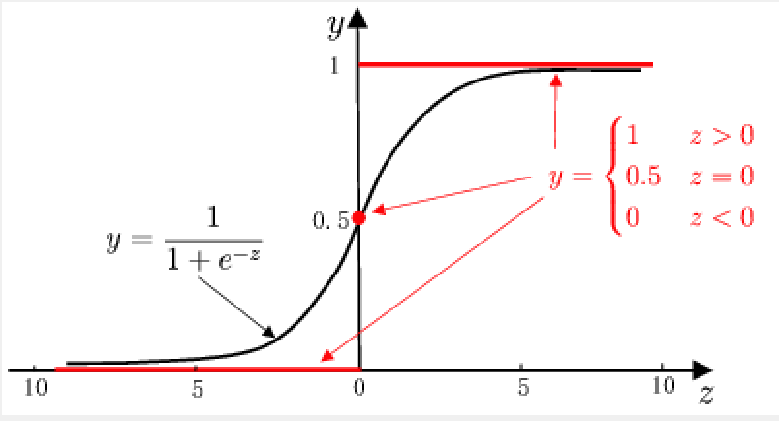
在这里插入图片描述

运用对数几率函数：
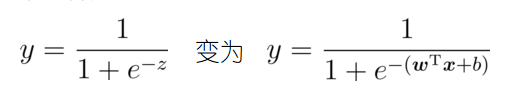
在这里插入图片描述
对数几率（log odds）

样本作为正例的相对可能性的对数

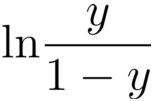
对数几率回归优点
无需事先假设数据分布
可得到“类别”的近似概率预测
可直接应用现有数值优化算法求取最优解

多分类学习

多分类学习方法

二分类学习方法推广到多类
利用二分类学习器解决多分类问题（常用）
- 对问题进行拆分，为拆出的每个二分类任务训练一个分类器
- 对于每个分类器的预测结果进行集成以获得最终的多分类结果

拆分策略

一对一（One vs. One, OvO）
一对其余（One vs. Rest, OvR）
多对多（Many vs. Many, MvM）

给定一个训练集有N个预测标签，将这N个类别两两配对，从而产生N(N-1)/2个分类结果，最终结果可通过投票产生：即把被预测得最多的类别作为最终分裂结果

拆分阶段

N个类别两两配对
- N(N-1)/2 个二类任务
各个二类任务学习分类器
- N(N-1)/2 个二类分类器

测试阶段

新样本提交给所有分类器预测
- N(N-1)/2 个分类结果
投票产生最终分类结果
- 被预测最多的类别为最终类别

一对其余

任务拆分

某一类作为正例，其他反例
- N 个二类任务
各个二类任务学习分类器
- N 个二类分类器

测试阶段

新样本提交给所有分类器预测
- N 个分类结果
比较各分类器预测置信度
- 置信度最大类别作为最终类别

两种策略比较

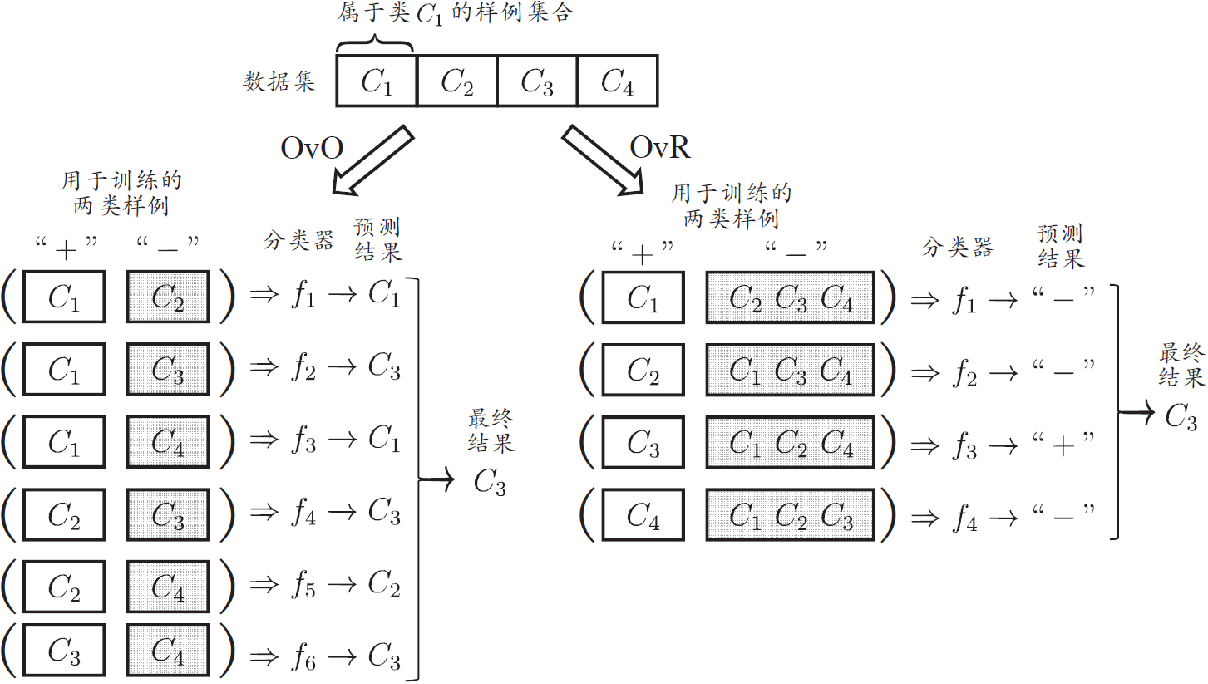
在这里插入图片描述
一对一

训练N(N-1)/2个分类器，存储开销和测试时间大
训练只用两个类的样例，训练时间短

一对其余

训练N个分类器，存储开销和测试时间小
训练用到全部训练样例，训练时间长

预测性能取决于具体数据分布，多数情况下两者差不多

多对多

多对多（Many vs Many, MvM）
若干类作为正类，若干类作为反类

纠错输出码（Error Correcting Output Code, ECOC）

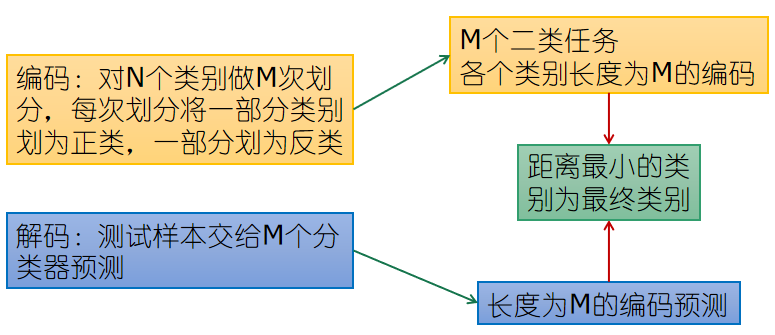
在这里插入图片描述
纠错输出码(Error Correcting Output Code, ECOC)

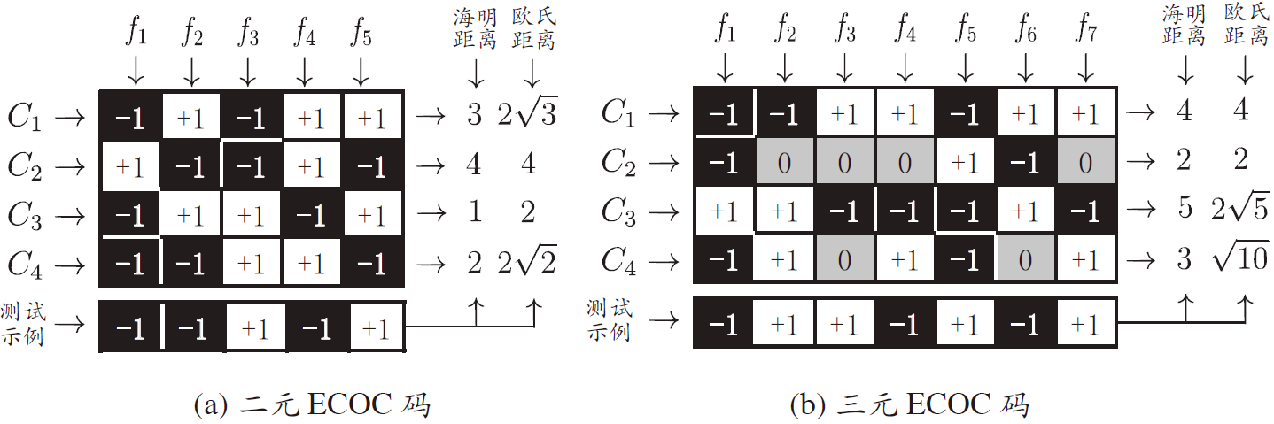
在这里插入图片描述

ECOC编码对分类器错误有一定容忍和修正能力，编码越长、纠错能力越强
对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强

类别不平衡

类别不平衡（class imbalance）

不同类别训练样例数相差很大情况（正类为小类）

在这里插入图片描述

再缩放

欠采样（undersampling）
- 去除一些反例使正反例数目接近（EasyEnsemble [Liu et al.,2009]）
过采样（oversampling）
- 增加一些正例使正反例数目接近（SMOTE [Chawla et al.2002]）
直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，将式 $y'/1-y' = y/1-y * m^-/m^+$ 嵌入到其决策过程中，称为阈值移动（threshold-moving）

优化提要

各任务下（回归、分类）各个模型优化的目标

最小二乘法：最小化均方误差
对数几率回归：最大化样本分布似然

参数的优化方法

最小二乘法：线性代数
对数几率回归：凸优化梯度下降、牛顿法

线性回归

线性回归是属于机器学习里面的监督学习，与分类问题不同的是，在回归问题中，其目标是通过对训练样本的学习，得到从样本特征到样本标签直接的映射，其中，在回归问题中，样本的标签是连续值（分类是离散值）。线性回归是一类重要的回归问题。在线性回归中，目标值与特征直接存在线性关系。

若线性回归方程得到多个解，下面哪些方法能够解决此问题？

获取更多的训练样本
选取样本有效的特征，使样本数量大于特征数
加入正则化项

线性回归分析中的残差（Residuals）

残差均值总是为零

线性回归分析中，目标是残差最小化。残差平方和是关于参数的函数，为了求残差极小值，令残差关于参数的偏导数为零，会得到残差和为零，即残差均值为零。

若下图展示了两个拟合回归线（A 和 B），原始数据是随机产生的。现在，我想要计算 A 和 B 各自的残差之和。注意：两种图中的坐标尺度一样。

关于 A 和 B 各自的残差之和，下列说法正确的是？

A 与 B 相同

A 和 B 中各自的残差之和应该是相同的。线性回归模型的损失函数为： $Loss=\sum(y'-(wxi+b))^2$
对损失函数求导，并令 ?Loss=0，即可得到 XW-Y=0，即残差之和始终为零。

波士顿房价预测

sklearn中已经提供了波斯顿房价数据集的相关接口，想要使用该数据集可以使用如下代码：

from sklearn import datasets

#加载波斯顿房价数据集
boston = datasets.load_boston()
#X表示特征，y表示目标房价
X = boston.data
y = boston.target

由数据集可以知道，每一个样本有13个特征与目标房价，而我们要做的事就是通过这13个特征来预测房价，我们可以构建一个多元线性回归模型，来对房价进行预测。

模型如下：

$y=b+w_1x_1+w_2x_2+...+w_nx_n$
$x_i$ ：第i个特征值， $w_i$ ：表示第i个特征对应的权重，b表示偏置，y是目标房价.

为了方便，我们稍微将模型进行变换：

$y=w_0x_0+w_1x_1+w_2x_2+...+w_nx_n$

其中 $x_0$ 等于1.

$Y = h e t a X$

$heta=(w_0, w_1,..,w_n)$
$X=(1,x_1,....,x_n)$

而我们的目的就是找出能够正确预测的多元线性回归模型，即找出正确的参数heta。

那么如何寻找呢？通常在监督学习里面都会使用这么一个套路，构造一个损失函数，用来衡量真实值与预测值之间的差异，然后将问题转化为最优化损失函数。 既然损失函数是用来衡量真实值与预测值之间的差异那么很多人自然而然的想到了用所有真实值与预测值的差的绝对值来表示损失函数。不过带绝对值的函数不容易求导，所以采用MSE(均方误差)作为损失函数，公式如下：

$Loss=\sum(y^i-p^i)^2/m$

线性回归的正规方程解

对线性回归模型，假设训练集中m个训练样本，每个训练样本中有n个特征，可以使用矩阵的表示方法，预测函数可以写为： $Y = h e t a X$

其损失函数可以表示为：
$Y-hetaX)^T(Y-hetaX)$

其中，标签Y为[m,1]的矩阵，训练特征X为[m,(n+1)]（n列特征+1列偏置）的矩阵，回归系数heta为[(n+1), 1]的矩阵，对heta求导，并令其导数等于0，可以得到: $X^T(Y-hetaX)=0$ 。

所以，最优解为： $heta=(X^TX)^{-1}X^TY$

这个就是正规方程解，我们可以通过最优方程解直接求得我们所需要的参数。

线性代数的知识

import numpy as np

def mse_score(y_predict,y_test):
    '''
    input:y_predict(ndarray):预测值
          y_test(ndarray):真实值
    ouput:mse(float):mse损失函数值
    '''
    #********* Begin *********#
    mse = np.mean((y_predict-y_test)**2)
    #********* End *********#
    return mse
class LinearRegression :
    def __init__(self):
        '''初始化线性回归模型'''
        self.theta = None
    def fit_normal(self,train_data,train_label):
        '''
        input:train_data(ndarray):训练样本
              train_label(ndarray):训练标签
        '''
        #********* Begin *********#
        # 特征值x水平拼接一列全为零的数（初始化偏置）
        x = np.hstack([np.ones((len(train_data),1)),train_data])
        # 计算权重的正规方程最优解
        self.theta = np.linalg.inv(x.T.dot(x)).dot(x.T).dot(train_label)
        #********* End *********#
        return self.theta
    def predict(self,test_data):
        '''
        input:test_data(ndarray):测试样本
        '''
        #********* Begin *********#
        # 特征值x水平拼接（左右拼接）一列全为零的数（初始化偏置）
        x = np.hstack([np.ones((len(test_data),1)),test_data])
        
        return x.dot(self.theta)  # WX=Y：预测值
        #********* End *********#

np.ones((5,1))  # 维度必须()或[]
np.ones([5,1])

array([[1.],
       [1.],
       [1.],
       [1.],
       [1.]])

性能评估

MSE

MSE （Mean Squared Error）叫做均方误差,公式如下：
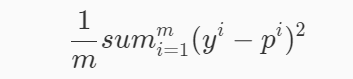
在这里插入图片描述

mse = np.mean((y_predict-y_test)**2)

在这里插入图片描述

RMSE（Root Mean Squard Error）均方根误差，公式如下：
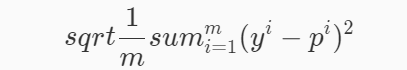
在这里插入图片描述

rmse = np.sqrt(np.mean((y_predict-y_test)**2))

RMSE其实就是MSE开个根号。有什么意义呢？其实实质是一样的。只不过用于数据更好的描述。

例如：要做房价预测，每平方是万元，我们预测结果也是万元。那么差值的平方单位应该是千万级别的。那我们不太好描述自己做的模型效果。怎么说呢？我们的模型误差是多少千万？于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的了，在描述模型的时候就说，我们模型的误差是多少万元。

MAE

MAE(平均绝对误差)，公式如下：

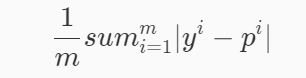
在这里插入图片描述
MAE虽然不作为损失函数，确是一个非常直观的评估指标，它表示每个样本的预测标签值与真实标签值的L1距离。

mae = np.mean((y_predict-y_test))

在这里插入图片描述

R-Squared

上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价那么误差单位就是万元。数子可能是3，4，5之类的。那么预测身高就可能是0.1，0.6之类的。没有什么可读性，到底多少才算好呢？不知道，那要根据模型的应用场景来。

看看分类算法的衡量标准就是正确率，而正确率又在0～1之间，最高百分之百。最低0。如果是负数，则考虑非线性相关。很直观，而且不同模型一样的。那么线性回归有没有这样的衡量标准呢？

R-Squared就是这么一个指标，公式如下：
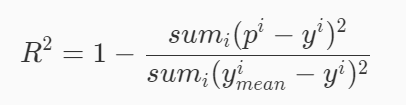
在这里插入图片描述
$R^2=1-MSE/Var$

r2 =1-mse_score(y_predict,y_test)/np.var(y_test)
r2 = 1- np.mean((y_predict-y_test)**2)/np.var(y_test)

np.var(y_test)：计算方差
在这里插入图片描述

scikit-learn线性回归实践

import pandas as pd
from sklearn.linear_model import LinearRegression

#获取训练数据
train_data = pd.read_csv('./step3/train_data.csv')
#获取训练标签
train_label = pd.read_csv('./step3/train_label.csv')
train_label = train_label['target']
#获取测试数据
test_data = pd.read_csv('./step3/test_data.csv')
lr = LinearRegression()
#训练模型
lr.fit(train_data,train_label)
#获取预测标签
predict = lr.predict(test_data)
#将预测标签写入csv
df = pd.DataFrame({'result':predict}) 
df.to_csv('./step3/result.csv', index=False)

LinearRegression的构造函数中有两个常用的参数可以设置：

fit_intercept：是否有截据，如果没有则直线过原点，默认为Ture。
normalize：是否将数据归一化,默认为False。

LinearRegression类中的fit函数用于训练模型，fit函数有两个向量输入：

X：大小为 [样本数量,特征数量] 的ndarray，存放训练样本
Y：值为整型，大小为 [样本数量] 的ndarray，存放训练样本的标签值

LinearRegression类中的predict函数用于预测，返回预测值，predict函数有一个向量输入：

X：大小为 [样本数量,特征数量] 的ndarray，存放预测样本

更详细，请参考:【线性回归】案例：波士顿房价预测

正规方程

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error

def linear_model1():
    """
    线性回归:正规方程
    :return:None
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(正规方程)
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

    return None

梯度下降

def linear_model2():
    """
    线性回归:梯度下降法
    :return:None
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(特征方程)
    estimator = SGDRegressor(max_iter=1000)
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

    return None

癌细胞预测

逻辑回归是在线性回归的输出结果加上激活函数进行非线性的映射，如：sigmoid函数。

$σ(t)=1/(1+e^{?t})$

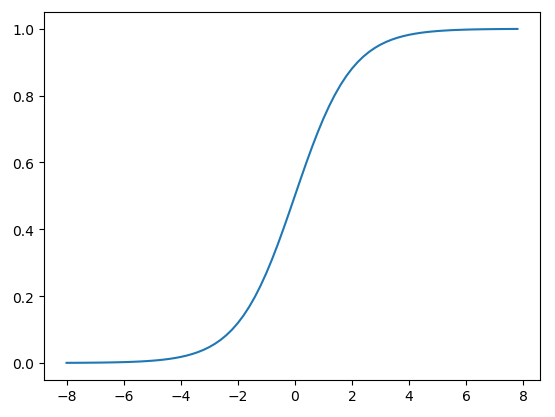
在这里插入图片描述
值域为(0,1)。

import numpy as np

def sigmoid(t):
    '''
    完成sigmoid函数计算
    :param t: 负无穷到正无穷的实数
    :return: 转换后的概率值
    :可以考虑使用np.exp()函数
    '''
    return 1 / (1 + np.exp(-t))

为什么需要损失函数？

训练逻辑回归模型的过程其实与之前学习的线性回归一样，就是去寻找合适的 $W^T$ 和 $b$ 使得模型的预测结果与真实结果尽可能一致。所以就需要一个函数能够衡量模型拟合程度的好坏，也就是说当模型拟合误差越大的时候，函数值应该比较大，反之应该比较小，这就是损失函数。

逻辑回归的损失函数

我们已经知道了逻辑回归计算出的样本所属类别的概率
$p=σ(W^T x+b)$ ，样本所属列表的判定条件为：
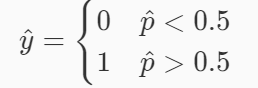
在这里插入图片描述
所以逻辑回归的损失函数如下，其中 cost 表示损失函数的值， y 表示样本的真实类别：

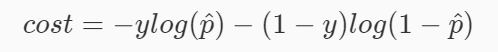
这个式子其实很好理解，当样本的真实类别为 1 时，式子就变成了 $c o s t = ? l o g (p)$ 。此时函数图像如下：

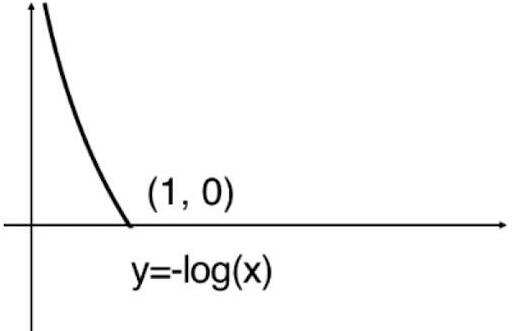
从图像能看出当样本的真实类别为1的前提下，p越大，损失函数值就越小。因为p越大就越说明模型越认为该样本的类别为 1。

当样本的真实类别为 0 时，式子就变成了 $c o s t = ? l o g (1 ? p)$ 。此时函数图像如下：
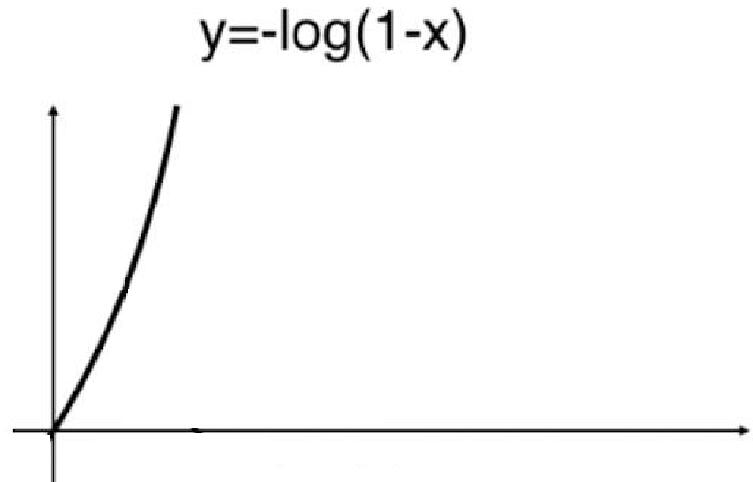
在这里插入图片描述
从图像能看出当样本的真实类别为0的前提下，p越大，损失函数值就越大。因为p越大就越说明模型越认为该样本的类别为 1。

在这里插入图片描述
逻辑回归的损失函数可以写成如下形式：

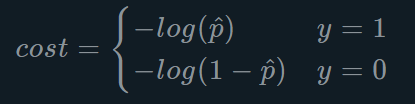
损失值能够衡量模型在训练数据集上的拟合程度
sigmoid函数的输入越大，输出就越大
训练的过程，就是寻找合适的参数使得损失函数值最小的过程

sigmoid函数(对数几率函数)相对于单位阶跃函数有哪些好处？

sigmoid函数可微分
sigmoid函数处处连续

逻辑回归的优点有哪些？

可以用现有的数值优化算法求解

梯度下降

梯度：梯度的本意是一个向量，由函数对每个参数的偏导组成，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向变化最快，变化率最大。

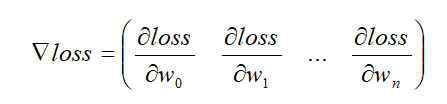
在这里插入图片描述
梯度下降算法原理

算法思想：梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使损失函数最小化。假设你迷失在山上的迷雾中，你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡。这就是梯度下降的做法：通过测量参数向量 θ 相关的损失函数的局部梯度，并不断沿着降低梯度的方向调整，直到梯度降为 0 ，达到最小值。

为了寻求损失函数的最小值，不断沿着函数变化最快的地方（梯度），降低梯度直到梯度为0即是函数最小值，即可获得最优参数向量。

梯度下降公式如下：

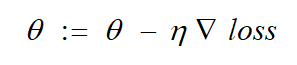
在这里插入图片描述
对应到每个权重公式为：

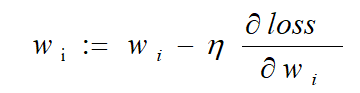
在这里插入图片描述
其中 η 为学习率，是 0 到 1 之间的值，是个超参数，需要我们自己来确定大小。

算法原理：

在传统机器学习中，损失函数通常为凸函数，假设此时只有一个参数，则损失函数对参数的梯度即损失函数对参数的导数。如果刚开始参数初始在最优解的左边，
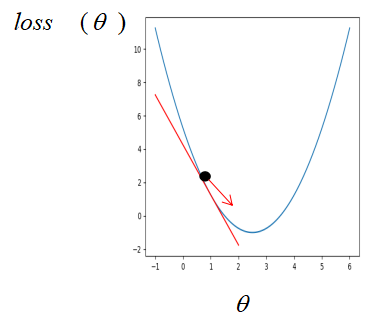
在这里插入图片描述
很明显，这个时候损失函数对参数的导数是小于 0 的（函数递减），而学习率是一个 0 到 1 之间的数，此时按照公式更新参数，初始的参数减去一个小于 0 的数是变大，也就是在坐标轴上往右走，即朝着最优解的方向走。同样的，如果参数初始在最优解的右边，

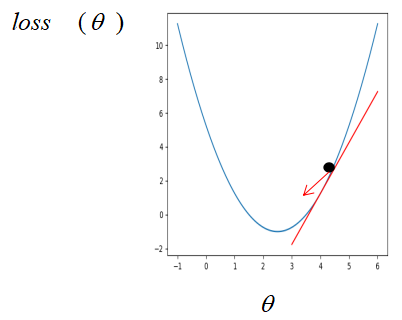
在这里插入图片描述
此时按照公式更新，参数将会朝左走，即最优解的方向。所以，不管刚开始参数初始在何位置，按着梯度下降公式不断更新，参数都会朝着最优解的方向走。

梯度下降算法流程

随机初始参数；
确定学习率；
求出损失函数对参数梯度；
按照公式更新参数；
重复 3 、 4 直到满足终止条件（如：损失函数或参数更新变化值小于某个阈值，或者训练次数达到设定阈值）。

import numpy as np
import warnings
warnings.filterwarnings("ignore")

def gradient_descent(initial_theta,eta=0.05,n_iters=1000,epslion=1e-8):
    '''
    梯度下降
    :param initial_theta: 参数初始值，类型为float
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :param epslion: 容忍误差范围，类型为float
    :return: 训练后得到的参数
    ''' 
    theta = initial_theta
    for i in range(n_iters):
        gradient = 2*(theta-3)  # 梯度计算
        last_theta = theta  # 记录上一次的参数向量
        theta = theta - eta*gradient  # 梯度下降
        # 如果损失函数值或参数更新变化值小于阈值则提前结束（Loss值变化不明显）
        if (abs(theta-last_theta) < epslion):
            break
    return theta

动手实现逻辑回归 - 癌细胞精准识别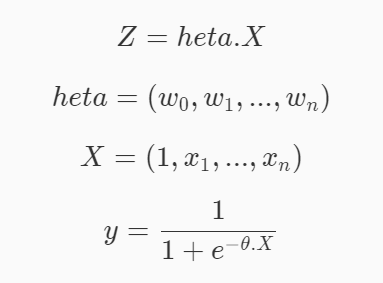 在这里插入图片描述
损失函数对每个参数的偏导：

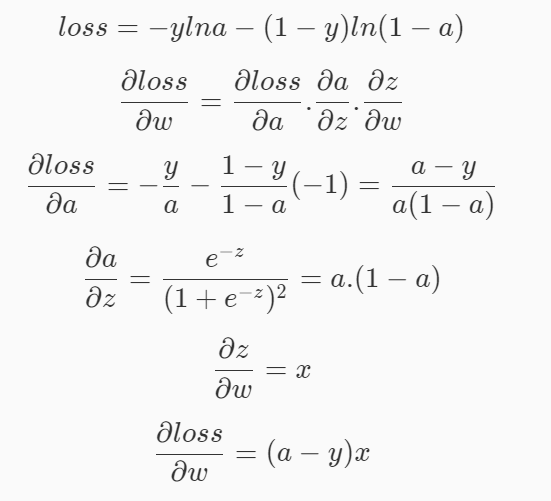
于是，在逻辑回归中的梯度下降公式如下：
$w_i=w_i-n(a-y)xi$

import numpy as np
import warnings
warnings.filterwarnings("ignore")

def sigmoid(x):
    '''
    sigmoid函数
    :param x: 转换前的输入
    :return: 转换后的概率
    '''
    return 1/(1+np.exp(-x))

def fit(x,y,eta=1e-3,n_iters=10000):
    '''
    训练逻辑回归模型
    :param x: 训练集特征数据，类型为ndarray
    :param y: 训练集标签，类型为ndarray
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :return: 模型参数，类型为ndarray
    '''
    # 初始化权重，x.shape()形状(m,n):m行n列，n为特征数
    theta = np.zeros(x.shape[1])  # theta形状(n,)
    i = 0
    while i < n_iters:
    	# 计算梯度
    	gradient = (sigmoid(x.dot(theta))-y).dot(x)
    	# 权重梯度下降，相当于沿着函数递减的方向移动x轴的值即theta
    	# 请结合高等数学来思考
    	theta = theta - eta*gradient
    	i += 1
    return theta

计算梯度:gradient = (sigmoid(x.dot(theta))-y).dot(x)代码演示：

# 生成4个数据，每一条数据3个特征值
x = np.arange(1,13).reshape((4, 3))
array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])
       
x.shape
(4, 3)

theta = np.ones(x.shape[1])
array([1., 1., 1.])

# 初始化y值
y = np.ones(x.shape[0])
array([1., 1., 1., 1.])

# x的每一行都和theta进行向量点积得到预测的y值
x.dot(theta)
array([ 6., 15., 24., 33.])

应该懂了嘛！

逻辑回归api介绍

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)
- solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}，
  - 默认: 'liblinear'；用于优化问题的算法。
  - 对于小数据集来说，“liblinear”是个不错的选择，而“sag”和’saga'对于大型数据集会更快。
  - 对于多类问题，只有'newton-cg'， 'sag'， 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
- penalty：正则化的种类
- C：正则化力度，默认为 1.0 ，越小代表正则化越强；

默认将类别数量少的当做正例

LogisticRegression方法相当于SGDClassifier(loss=“log”, penalty=" "),SGDClassifier实现了一个普通的随机梯度下降学习。而使用LogisticRegression(实现了SAG)

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression


# 1.获取数据
names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']

data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                  names=names)

# 2.基本数据处理
# 2.1 缺失值处理
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# 2.2 确定特征值,目标值
x = data.iloc[:, 1:10]
x.head()
y = data["Class"]
y.head()
# 2.3 分割数据
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)

# 3.特征工程(标准化)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习(逻辑回归)
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

# 5.模型评估
y_predict = estimator.predict(x_test)
y_predict
estimator.score(x_test, y_test)

更多内容，请参考:【机器学习】逻辑回归算法

# 0.5~1之间，越接近于1约好
y_test = np.where(y_test > 2.5, 1, 0)

print("AUC指标：", roc_auc_score(y_test, y_predict)

AUC的概率意义是随机取一对正负样本，正样本得分大于负样本得分的概率
AUC的范围在[0, 1]之间，并且越接近1越好，越接近0.5属于乱猜
AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5<AUC<1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

手写数字识别

数据简介

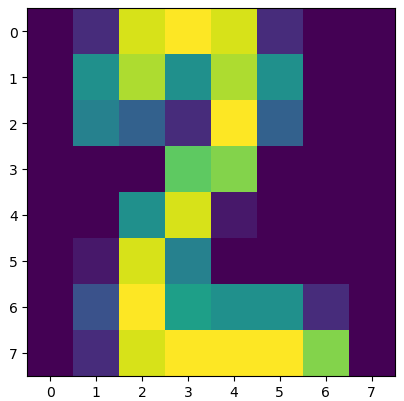
本关使用的是手写数字数据集，该数据集有 1797 个样本，每个样本包括 8*8 像素（实际上是一条样本有 64 个特征，每个像素看成是一个特征，每个特征都是float类型的数值）的图像和一个 [0, 9] 整数的标签。

比如下图的标签是 2 ：

在这里插入图片描述

from sklearn import datasets
import matplotlib.pyplot as plt
# 加载数据集
digits = datasets.load_digits()
# X表示图像数据，y表示标签
X = digits.data
y = digits.target
# 将第233张手写数字可视化
plt.imshow(digits.images[232])

logreg = LogisticRegression(solver='lbfgs',max_iter =10,C=10)
logreg.fit(X_train, Y_train)
result = logreg.predict(X_test)

train_image：训练集图像，类型为ndarray，shape=[-1, 8, 8]；

from sklearn.linear_model import LogisticRegression

def digit_predict(train_image, train_label, test_image):
    '''
    实现功能：训练模型并输出预测结果
    :param train_sample: 包含多条训练样本的样本集，类型为ndarray,shape为[-1, 8, 8]
    :param train_label: 包含多条训练样本标签的标签集，类型为ndarray
    :param test_sample: 包含多条测试样本的测试集，类型为ndarry
    :return: test_sample对应的预测标签
    '''
     # 训练集变形
     train_image = train_image.reshape(-1, 64)
     # 训练集标准化
     train_min = flat_train_image.min()
     train_max = flat_train_image.max()
     train_image = (train_image-train_min)/(train_max-train_min)
     # 测试集变形
     test_image = test_image.reshape((-1, 64))
     # 测试集标准化
     test_min = test_image.min()
     test_max = test_image.max()
     test_image = (test_image - test_min) / (test_max - test_min)
     # 训练--预测
     rf = LogisticRegression(C=4.0)  # C：正则化力度，默认为 1.0 ，越小代表正则化越强；
     rf.fit(train_image, train_label)
    
     return rf.predict(test_image)

X'=(x?min)/(max??min)

特征预处理中的归一化处理：

归一化首先在特征（维度）非常多的时候，可以防止某一维或某几维对数据影响过大，也是为了把不同来源的数据统一到一个参考区间下，这样比较起来才有意义，其次可以程序可以运行更快。

例如：一个人的身高和体重两个特征，假如体重50kg，身高175cm,由于两个单位不一样，数值大小不一样。如果比较两个人的体型差距时，那么身高的影响结果会比较大，因此在做计算之前需要先进行归一化操作。

请参考:【机器学习】带你搞懂什么是特征工程？(特征抽取&特征预处理&特征选择&数据降维)

第四章：决策树

基本流程

决策树基于树结构来进行预测

决策过程中提出的每个判定问题都是对某个属性的“测试”
决策过程的最终结论对应了我们所希望的判定结果
每个测试的结果或是导出最终结论，或者导出进一步的判定问题，其考虑范围是在上次决策结果的限定范围之内
从根结点到每个叶结点的路径对应了一个判定测试序列

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树

划分选择

决策树学习的关键在于如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”(purity)越来越高

经典的属性划分方法：

信息增益
增益率
基尼指数

信息增益

“信息熵”是度量样本集合纯度最常用的一种指标，假定当前样本集合D中第k类样本所占的比例为 $p_k$ ，则D的信息熵定义为：
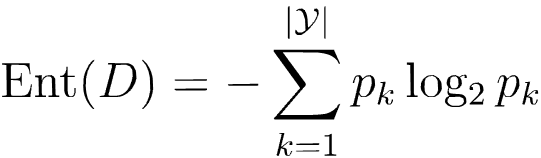
在这里插入图片描述
Ent(D)的值越小，则D的纯度越高。

计算信息熵时约定：若p=0， $p*log2^p = 0$ .
Ent(D)的最小值为0，最大值 $log2^y$ .

在这里插入图片描述

一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大
ID3决策树学习算法[Quinlan, 1986]以信息增益为准则来选择划分属性

信息增益实例

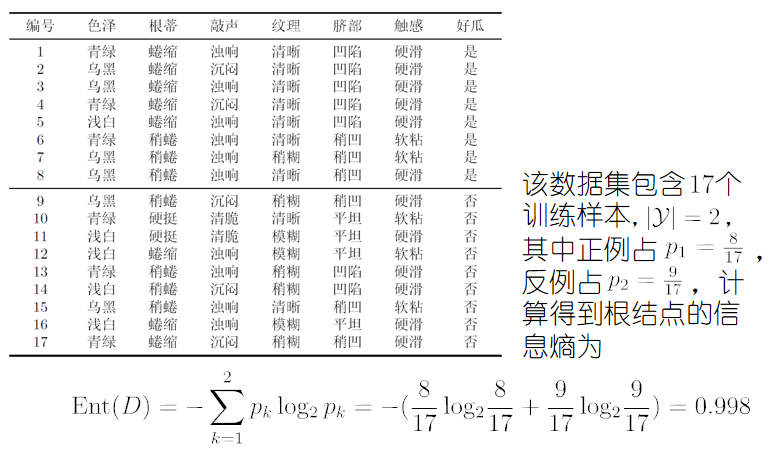
在这里插入图片描述

存在的问题

若把“编号”也作为一个候选划分属性，则其信息增益一般远大于其他属性。显然，这样的决策树不具有泛化能力，无法对新样本进行有效预测。

信息增益对可取值数目较多的属性有所偏好

增益率

在这里插入图片描述
存在的问题：

增益率准则对可取值数目较少的属性有所偏好

C4.5 [Quinlan, 1993]使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选取增益率最高的

基尼指数

数据集D的纯度可用“基尼值”来度量：

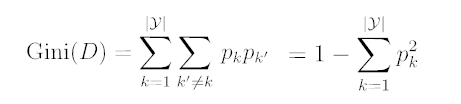
在这里插入图片描述

反映了从D中随机抽取两个样本，其类别标记不一致的概率.
Gini(D)：越小，数据集D的纯度越高.

在这里插入图片描述
CART [Breiman et al., 1984]采用“基尼指数”来选择划分属性

剪枝处理

为什么剪枝？

“剪枝”是决策树学习算法对付“过拟合”的主要手段
可通过“剪枝”来一定程度避免因决策分支过多，以致于把训练集自身的一些特点当做所有数据都具有的一般性质而导致的过拟合

剪枝的基本策略

预剪枝
后剪枝

判断决策树泛化性能是否提升的方法

留出法：预留一部分数据用作“验证集”以进行性能评估

预剪枝

决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点记为叶结点，其类别标记为训练样例数最多的类别

针对上述数据集，基于信息增益准则，选取属性“脐部”划分训练集。分别计算划分前（即直接将该结点作为叶结点）及划分后的验证集精度，判断是否需要划分。若划分后能提高验证集精度，则划分，对划分后的属性，执行同样判断；否则，不划分

预剪枝的优缺点

优点

降低过拟合风险
显著减少训练时间和测试时间开销

缺点

欠拟合风险：有些分支的当前划分虽然不能提升泛化性能，但在其基础上进行的后续划分却有可能导致性能显著提高。预剪枝基于“贪心”本质禁止这些分支展开，带来了欠拟合风险

后剪枝

先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点

后剪枝的优缺点

优点

后剪枝比预剪枝保留了更多的分支，欠拟合风险小，泛化性能往往优于预剪枝决策树

缺点

训练时间开销大：后剪枝过程是在生成完全决策树之后进行的，需要自底向上对所有非叶结点逐一考察

ID3，C4.5和CART算法对比

相同点：都采用贪心方法，以自顶向下递归的分治方式构造，随着树的构建，训练集递归地被划分为子集

不同点：

ID3算法基于信息增益为准则来选择划分属性，依赖于特征数目多的特征，没有考虑少特征和不完整数据，抗噪性差，容易产生过拟合.
C4.5算法基于增益率准则来选择划分属性，使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选取增益率最高的，对可取值数目较少的属性有所偏好。

第五章神经网络

试推导出BP算法中的更新公式

推导过程就是符号有点复杂，其他的就是高数里的链式求导。

Some note for comprehend

输出层与输入层之间的一层神经元称为隐层或隐含层，隐含层和输出层神经元都是拥有激活函数的神经元.
多层前馈神经网络：每层神经元与下层神经元全互联，神经元之间不存在同层连接，也不存在跨层连接.
输出层神经元与输出层神经元对信号进行加工，最终结果由输出神经元输出. 换言之，输入层只接受输入，不进行函数处理，隐层与输出层包含功能神经元.
包含一层隐层为两层神经网络（西瓜书为单隐层网络）
神经网络的学习过程，就是训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值；换言之，神经网络“学”到的东西，蕴含在连接权与阈值中.
个人理解神将网络就是由多个线性回归组成每一层网络的神经元，具有不同的权重与阈值（具有不同的功能），每一层加入不同的激活函数，进行非线性处理。

BP误差逆传播算法（error BackPropagation）

第六章：支持向量机

什么是支持向量机

支持向量机也称为“支持向量网络”，是一种判别式机器学习分类算法。它使用决策边界（超平面）一次将数据点分类两类（这并不意味着它只是一个二进制分类器，一次将数据分为两类）支持向量分类器的主要目标是找到“最佳超平面”（决策边界）。

试析SVM 对噪声敏感的原因

参考1：

SVM 的特性就是"支持向量" .即线性超平面只由少数"支持向量"所决定.若噪声成为了某个"支持向量"――这是非常有可能的.那么对整个分类的影响是巨大的.反观对率回归,其线性超平面由所有数据共同决定,因此一点噪声并无法对决策平面造成太大影响.

参考2：

因为SVM最终只用到了若干支持向量来生成分类的超平面,如果噪声更好成为支持向量,则整个超平面的划分就会有问题.而噪声往往又都是outlier离群点,容易成为支持向量.

参考3：

SVM的基本形态是一个硬间隔分类器，它要求所有样本都满足硬间隔约束（即函数间隔要大于1)
当数据集中存在噪声点但是仍然满足线性可分的条件时,SVM为了把噪声点也划分正确，超平面就会向另外一个类的样本靠拢,这就使得划分超平面的几何间距变小,从而降低了模型的泛化性能。
当数据集因为存在噪声点而导致已经无法线性可分时,此时就使用了核技巧,通过将样本映射到高维特征空间使得样本线性可分，这样就会得到—个复杂模型,并由此导致过拟合（原样本空间得到的划分超平面会是弯弯曲曲的，它确实可以把所有样本都划分正确，但得到的模型只对训练集有效)，泛化能力极差。
当数据集因为存在噪声点而导致已经无法线性可分时,此时就使用了核技巧,通过将样本映射到高维特征空间使得样本线性可分，这样就会得到—个复杂模型,并由此导致过拟合（原样本空间得到的划分超平面会是弯弯曲曲的，它确实可以把所有样本都划分正确，但得到的模型只对训练集有效)，泛化能力极差。

核函数的作用

隐含着一个从低维空间到高维空间的映射，这个映射可以把低维空间中的线性不可分的两类点变成线性可分的.

正则化

正则化的主要作用是防止过拟合，对模型添加正则化项可以限制模型的复杂度，使模型在复杂度和性能能达到平衡.

常用方法：有L1正则化和L2正则化。L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓“惩罚”是指对损失函数中的某些参数做一些限制.

L1正则化模型：Lasso回归

L2正则化模型：Ridge回归（岭回归）

第七章：贝叶斯分类器

第八章：集成学习

Boosting&Bagging

Boosting：个体学习器存在强依赖关系，必须串行生成的序列化方法.

Bagging和随机森林（RF）：个体学习器间不存在强依赖关系，可同时生成并行化方法.

区别：

1. 训练样本

Boosting：每一轮的训练集都是原始训练集，只是每次训练后会根据本轮的训练结果调整训练集中的各个样本的权重，调整完权重的训练集用于下一轮的训练.
Bagging：每个训练集都是以原始训练集中有放回的选取出来的，每个训练集各不相同且相互独立.

2. 样本权重不同

Boosting：根据每轮的训练不断调整权值，分类错误的样本拥有更高的权值.
Bagging：使用Boostraping的方式均匀抽样，每个样例权重相等

3. 分类器权重

Boosting：每个弱分类器都有响应的权重，对分类误差小的分类器有更大的权重，结果是基分类器加权结合.
Bagging：所有若分类器权重相同，对分类任务使用简单投票法，对回归任务使用简单平均法决定最终结果.

4. 并行计算

Boosting：各个预测函数只能顺序生成，因为每一个模型的训练永远建立在前一个模型的基础上.
Bagging：各个预测函数可以并行生成，因为数据集相互独立，每个模型之间也独立，没有序列关系.

5. 从偏差-方差

Boosting关注于降低偏差，Bagging关于降低方差

第九章：聚类

聚类任务

在“无监督学习”任务中研究最多、应用最广.
聚类目标：将数据集中的样本划分为若干个通常不相交的子集（“簇”，cluster）.
聚类既可以作为一个单独过程（用于找寻数据内在的分布结构），也可作为分类等其他学习任务的前驱过程.

“簇”可能对应于一些潜在的概念(类别)，如：“浅色瓜”，“有籽瓜”；这些概念对聚类算法而言是事先未知的，聚类过程能自动形成簇结构，簇所对应的概念语义由使用者来把握和命名.

第十章：降维与度量学习

降维

降维是将训练数据中的样本从高维空间转换到低位空间，该过程与信息论中有损压缩概念密切相关，不存在完全无损的降维。
降维是指通过保留一些比较重要的特征，去除一些冗余的特征，减少数据特征的维度。而特征的重要性取决于该特征能够表达多少数据集的信息，也取决于使用什么方法进行降维。一般情况会先使用线性的降维方法再使用非线性的降维方法，通过结果去判断哪种方法比较合适。

降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。

在哪里用到降维？

1）特征维度过大，可能会导致过拟合时

2）某些样本数据不足的情况（缺失值很多）

3）特征间的相关性比较大时

降维的好处？

（1）节省存储空间；

（2）加速计算速度，维度越少，计算量越少，并且能够使用那些不适合于高维度的算法；

（3）去除一些冗余的特征（原数据中既有平方米和平方英里的特征–即相关性大的特征）

（4）便于观察和挖掘信息（如将数据维度降到2维或者3维使之能可视化）

（5）特征太多或者太复杂会使得模型过拟合。

总结

单从机器学习角度来说：想要学好ML还是需要下更多功夫去钻研的。
单从考试角度来说：想考个及格/80+还是不难的，毕竟考试比较水，大家都懂。
考试既然水，分数就无所谓高低，重要的是我们学了多少东西。
如果看到这里，首先恭喜你与我同在，提前祝你考一个好的成绩。
如果有用的话，小伙伴帮忙点赞/打赏，算是对俺无私分享的支持与鼓励。
再次感谢大家的支持与陪伴，感谢其他学霸/大佬对此文的贡献，我仅仅是一个文字搬运工，分享快乐。

加油!

感谢!

努力!

数据结构与算法最新文章

【力扣106】从中序与后续遍历序列构造二叉

leetcode 322 零钱兑换

哈希的应用：海量数据处理

动态规划|最短Hamilton路径

华为机试_HJ41 称砝码【中等】【menset】【

【C与数据结构】——寒假提高每日练习Day1

基础算法——堆排序

2023王道数据结构线性表--单链表课后习题部

LeetCode 之反转链表的一部分

【题解】lintcode必刷50题＜有效的括号序列

加:2021-12-13 13:06:58 更:2021-12-13 13:08:03

360图书馆购物三丰科技阅读网日历万年历 2024年11日历

-2024/11/26 16:35:08-

图片自动播放器
↓图片自动播放器↓

TxT小说阅读器
↓语音阅读,小说下载,古典文学↓

一键清除垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

网站联系: qq:121756557 email:121756557@qq.com IT数码

[数据结构与算法]【一起啃西瓜书】机器学习-期末复习（不挂科）

【一起啃西瓜书】机器学习-期末复习（不挂科）

前言

试卷题型

第一章：绪论

一般过程

任务

数据

训练集

验证集

监督学习

无监督学习

半监督学习

第二章：模型评估与选择

欠拟合与过拟合

评估方法

性能度量

错误率&精度

查准率&查全率

交叉验证

第三章：线性模型

线性回归&分类

基本形式

线性模型优点

参数/模型估计

对数线性回归

对数几率回归

多分类学习

一对其余

两种策略比较

类别不平衡

优化提要

线性回归

波士顿房价预测

线性回归的正规方程解

性能评估

MSE

MAE

R-Squared

scikit-learn线性回归实践

正规方程

梯度下降

癌细胞预测

梯度下降

逻辑回归api介绍

手写数字识别

第四章：决策树

基本流程

划分选择

信息增益

增益率

基尼指数

剪枝处理

预剪枝

后剪枝

ID3，C4.5和CART算法对比

第五章 神经网络

试推导出BP算法中的更新公式

Some note for comprehend

第六章：支持向量机

什么是支持向量机

试析SVM 对噪声敏感的原因

核函数的作用

正则化

第七章：贝叶斯分类器

第八章：集成学习

Boosting&Bagging

第九章：聚类

聚类任务

第十章：降维与度量学习

降维

总结

第五章神经网络