hello,今天给大家带来一道算法题。这道算法题,是我目前为止,见过最难的一道题。那么到底是怎样的一道算法题呢?如下:
题目:给定一个数组, 求如果排序之后, 相邻两数的最大差值。 要求时间复杂度O(N), 且要求不能用非基于比较的排序。
我查了一下,暂时没有找到一个在线OJ的链接,只能自己写一个对数器,手动测试了。

当初我看到这个题目的时候,说这怎么可能呢?在一个无序的数组中,求相邻两个数据的最大差值。可是我们都知道,现在基于比较的排序算法,最快也只能够达到O(N*logN)的水平,而题目明确限制时间复杂度要是O(N),所以想通过基于比较的排序,排序之后再进行遍历,时间复杂度肯定是达不到要求的。
有人可能也会想说,不是还有基于非比较的排序算法吗?比如计数排序、基数排序、桶排序。但是题目又明确规定了不能使用基于非比较的排序算法。
这样的话,想使用排序算法,进行排序,这条路肯定是行不通的。只能另外想其他的办法。
-------------------------------------------------------------------------------------------我是分割线-----------------------------------------------------------------------------------------
重头戏来了!!!整个代码的流程如下:
-
先遍历一遍数组,保存整个数组的最大值和最小值。
-
假设数组中一共有N个元素,那么我们就需要准备N+1个桶。
这每一个桶里面,可以存储一定范围内的数值,而具体可以存储多大范围内的数值,需要用公式去计算。比如:第一个桶存储0……9之间的数,第二个桶存储10……19的数……
-
我们再次遍历一遍数组,将每一个数,放入到相应的桶里。
解释:为什么需要进行以上这3个步骤???这是一个非常值得思考的问题!!!
由题可知,一共有N个数,但是我们准备了N+1个桶。也就是说我们将每个数放入相应的桶中,就算这N个数都在各自的桶里,无论怎么放入,始终会多出来1个空桶。
而我们会根据一下这个公式,将每个数放入相应的桶:(arr【i】- min)* N / (max - min)。
以上这个公式,就能够计算出i位置的数,应该放入哪一个桶里。根据公式计算,最小值一定会放到第一个桶里,最大值也一定会放到最后一个桶里。那么既然第一个和最后一个桶肯定是有数据的,也就是说明那个空桶肯定是中间的某一个桶。
正是因为这个空桶的存在,会将很多种计算的可能性直接抹杀掉。说的具体点,假设一个桶的存储数的范围是0~9,也就是这个桶能够存储10个数,既然有一个空桶的话,那么肯定最后的答案是大于10的。
那么既然大于10的话,这两个数肯定不会在同一个桶里。这样的话,我们就排除了桶里面两个数据的情况,只需要考虑相邻两个桶之间的数,才可能是最终的答案。
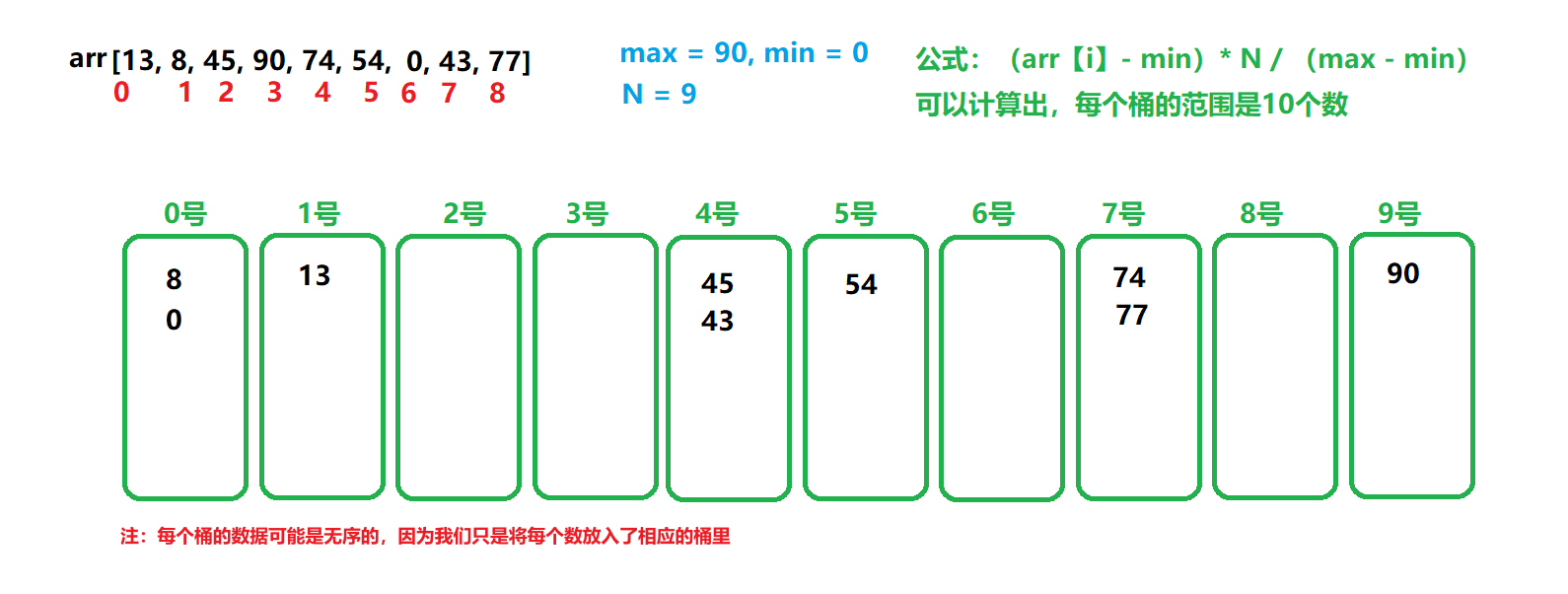
就如上图的形式,将所有的数据都放入相应的桶里。因为有空桶的存在,所以我们的答案必然是在两个不同桶之间的数据进行相减。而我们在进行相减的时候,只需要记录每个桶的最大值和最小值即可。也就是说,用后一个桶的最小值,减前一个桶的最大值。以这样的形式,循环N次,将每两个相邻的桶进行计算,就能得到最终的答案。
既然我们只需要每个桶里的最大值和最小值,那就准备两个数组maxs和mins,分别存储即可。代码如下:
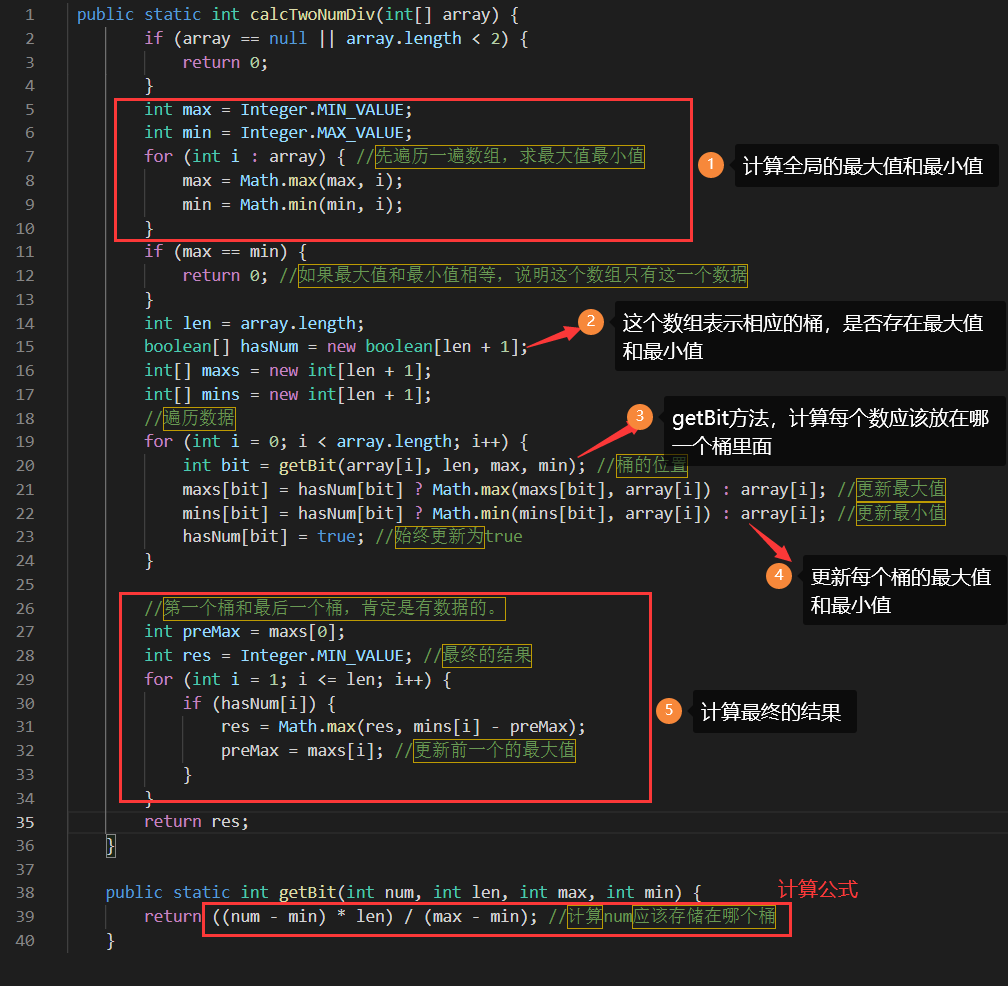
以上就是这道题的所有代码,代码不多,但是其中的算法思想我觉得真的是很厉害,很难想象出,想到这个方法的是什么人。
核心就在于那个空桶的存在,抹杀很多的可能性。使其最终的答案只可能存在于相邻两个桶之间的数。
提问:假设给定的某一个数组,算出来桶的数据后,只有一个是空桶。那么最终的答案就一定是这个空桶右边桶的数据减去左边桶的数据吗?
最后,我将整个代码全部放到下面,包括了一个对数器,用于测试以上代码的正确性。
import java.util.Arrays;
public class Code01_CalcTwoNumDiv {
public static void main(String[] args) {
int testTime = 5000; //测试次数
int N = 50; //数组长度
int range = 1000; //数据范围
boolean flag = true;
for (int i = 0; i < testTime; i++) {
int[] arr = generateArr(N, range);
int p1 = calcTwoNumDiv(arr);
int p2 = sortAfter(arr);
if (p1 != p2) {
flag = false;
break;
}
}
System.out.println(flag? "正确" : "错误");
}
public static int calcTwoNumDiv(int[] array) {
if (array == null || array.length < 2) {
return 0;
}
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int i : array) { //先遍历一遍数组,求最大值最小值
max = Math.max(max, i);
min = Math.min(min, i);
}
if (max == min) {
return 0; //如果最大值和最小值相等,说明这个数组只有这一个数据
}
int len = array.length;
boolean[] hasNum = new boolean[len + 1];
int[] maxs = new int[len + 1];
int[] mins = new int[len + 1];
//遍历数据
for (int i = 0; i < array.length; i++) {
int bit = getBit(array[i], len, max, min); //桶的位置
maxs[bit] = hasNum[bit] ? Math.max(maxs[bit], array[i]) : array[i]; //更新最大值
mins[bit] = hasNum[bit] ? Math.min(mins[bit], array[i]) : array[i]; //更新最小值
hasNum[bit] = true; //始终更新为true
}
//第一个桶和最后一个桶,肯定是有数据的。
int preMax = maxs[0];
int res = Integer.MIN_VALUE; //最终的结果
for (int i = 1; i <= len; i++) {
if (hasNum[i]) {
res = Math.max(res, mins[i] - preMax);
preMax = maxs[i]; //更新前一个的最大值
}
}
return res;
}
public static int getBit(int num, int len, int max, int min) {
return ((num - min) * len) / (max - min); //计算num应该存储在哪个桶
}
public static int sortAfter(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
Arrays.sort(arr);
int res = Integer.MIN_VALUE;
for (int i = 1; i < arr.length; i++) {
res = Math.max(res, arr[i] - arr[i - 1]);
}
return res;
}
public static int[] generateArr(int N , int range) {
int[] arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = (int)(Math.random() * range);
}
return arr;
}
}
好啦,本期更新就到此结束啊!!!我们下期见吧!!!