这个章节没听课很迷
集合的基本概念:
1.集合的成员必须互不相同,成员一般是无序的,没有先后次序的关系
2.表示方法:{1,2,3,4,5,6,7,8,9,10}
目录
集合的存储结构有两种:顺序存储与链式存储
顺序存储结构
定义代码实现(利用vector)
class Set
{
public:
virtual void makeEmpty() = 0;
virtual bool addMember(int x) = 0;
virtual bool delMember(int x) = 0;
// virtual void intersect(Set & r) = 0 ;
// virtual void union(Set & r) = 0 ;
// virtual void difference(Set & r) = 0 ;
virtual bool contains(int x)=0;
//其他方法的声明;
};
//组合复用vector来实现集合
class VectorSet : public Set
{
public:
VectorSet()
{ setSize = 0 ;
}
virtual void makeEmpty()
{ setSize = 0;
elem.clear();
}
private:
int setSize; //集合元素数目
vector<int> elem;
}
由于课程要求,我就实现集合的增删查并交
增
virtual bool addMember(int x)
{ //要考虑集合中没有重复元素。
vector<int>::iterator pos; //迭代器
pos = find(elem.begin(),elem.end(),x);
if (pos == elem.end())
{
++setSize;
elem.push_back(x);
return true;
}
else
return false ; //元素已经在集合中,添加失败
}
删(vector删除一个元素用erase()函数)
virtual bool delMember(int x)
{
vector<int>::iterator pos;
pos = find(elem.begin(),elem.end(),x);//找到x的位置
if (pos != elem.end())
{
elem.erase(pos); //删除该位置的元素
--setSize;
return true;
}
else
return flase;
}查
virtual bool contains(int x)
{
vector<int>::iterator pos;
pos = find(elem.begin(),elem.end(),x);
if (pos == elem.end())
return false;
else
return true;
}
并
void Union ( Vectorset& LA,Vectorset& LB ) {
int n1 = LA.setsize, n2 = LB.setsize;
int i, k, x;
for ( i = 0; i < n2; i++ ) {
x = LB.elem[i]; //在LB中取一元素
k = LA.contains(x); //在LA中搜索它
if (k == 0) //若在LA中未找到插入它
{
LA.addMember(x); LA.setsize++;
}
//插入到第n个表项位置
}
}交
void Intersection( Vectorset& LA,Vectorset& LB ) {
int n1 = LA.setsize;
int i=0, k, x;
while(i<n1){
x=LA.elem[i];
k = LB.contains(x); //在LA中搜索它
if (k == 0) //若在LA中未找到插入它
{
LA.delMember(x);
LA.setsize--;
}
}
}链式结构
也可以实现增删查并交
下面这个链式集合默认实现了排序。。。
class Set
{
public:
virtual void makeEmpty() = 0;
virtual bool addMember(int x) = 0;
virtual bool delMember(int x) = 0;
// virtual void intersect(Set & r) = 0 ;
// virtual void union(Set & r) = 0 ;
// virtual void difference(Set & r) = 0 ;
virtual bool contains(int x)=0;
//其他方法的声明;
};
template <class T>
struct LinkNode { //链表结点类的定义
T data; //数据域
LinkNode<T> * link; //链指针域
};
template <class T>
class ListSet : public Set
{
public:
ListSet() { first = new LinkNode<T>; } //构造函数
ListSet(T x) { first = new LinkNode<T>(x); }
virtual void makeEmpty();
protected:
LinkNode<T> * first; //表头指针
}
增
template <class T>
bool LinkedSet<T>::addMember(const T& x) {
//把新元素x加入到集合之中
LinkNode<T> *p = first->link, *pre = first;
while (p != NULL && p->data < x) //当data等于x时退出,循链扫描
{
pre = p;
p = p->link;
}
if (p != NULL && p->data == x)
return false; //集合中已有此元素, 不加入
LinkNode<T> *s = new LinkNode(x); //创建结点
s->link = p;
pre->link = s; //链入
if (p == NULL)
last = s; //链到链尾时改链尾指针
return true;
};删
template <class T>
bool LinkedSet<T>::delMember (const T& x) {
//把集合中成员x删去
LinkNode<T> *p = first->link, *pre = first;
while (p != NULL && p->data < x) //循链扫描
{
pre = p;
p = p->link;//快慢指针
}
if (p != NULL && p->data == x) { //找到,可删
pre->link = p->link; //利用前后指针进行删除
if (p == last)
last = pre; //删链尾时改尾指针
delete p; //删除含x结点
return true;
}
else
return false; //集合中无此元素
};查
template <class T>
bool LinkedSet<T>::contains(const T& x) {
//把集合中成员x删去
LinkNode<T> *p = first->link, *pre = first;
while (p != NULL && p->data < x) //循链扫描
{
pre = p;
p = p->link;//快慢指针
}
if (p != NULL && p->data == x) { //找到
return true;
}
else
return false; //集合中无此元素
};并
和上面的顺序结构的集合的'并'很像
主要思想是,先进行LA中链表的循环(到link指针为空截止)
{
每次取出LA的一个节点,在LB链表中查找,若查找到就continue继续下一步
若未查找到就插入到LB链表末尾
}
交
(快慢指针在链表操作的作用很高效,恰好就可以找到某节点的前驱节点)
这个交就要利用快慢指针进行删除。。
主要思想是,先进行LA中链表的循环(到link指针为空截止)
{
每次取出LA的一个节点,在LB链表中查找,
若查找到就在LB链表删除掉这个节点
若未查找到continue继续下一步
}
并查集
即将编号为1…N的N个对象划分为不相交集合,在每个集合中,选择其中某个元素代表所在集合。
? 并查集是一种树型的数据结构,用于处理一些不相交集合的合并问题。
? 并查集的主要操作有(考点)
? 1-合并两个不相交集合(合并过程)
? 2-判断两个元素是否属于同一个集合(查找过程)------Kruskal算法(图最小生成树)
? 3-路径压缩
例子:?
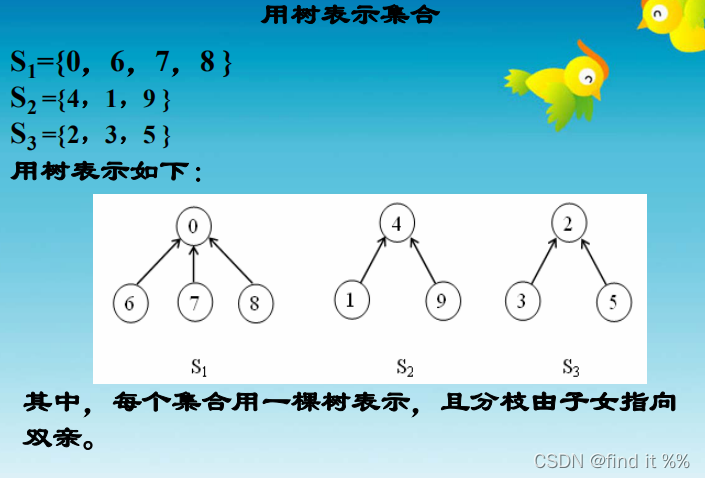
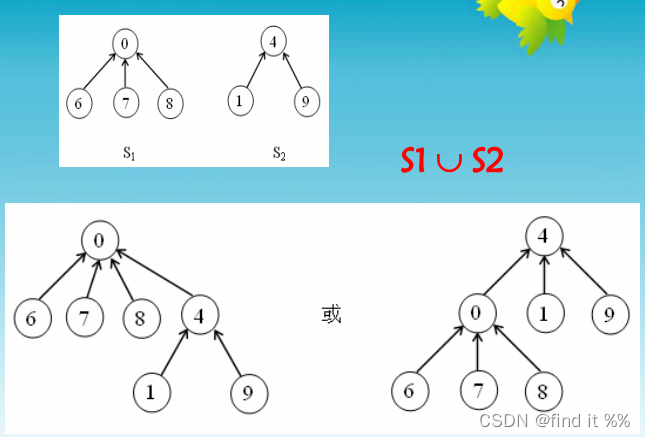
并查集这篇文章很好,我直接转了