题目描述

题目简单明了,我们直接给题解。
常规解法

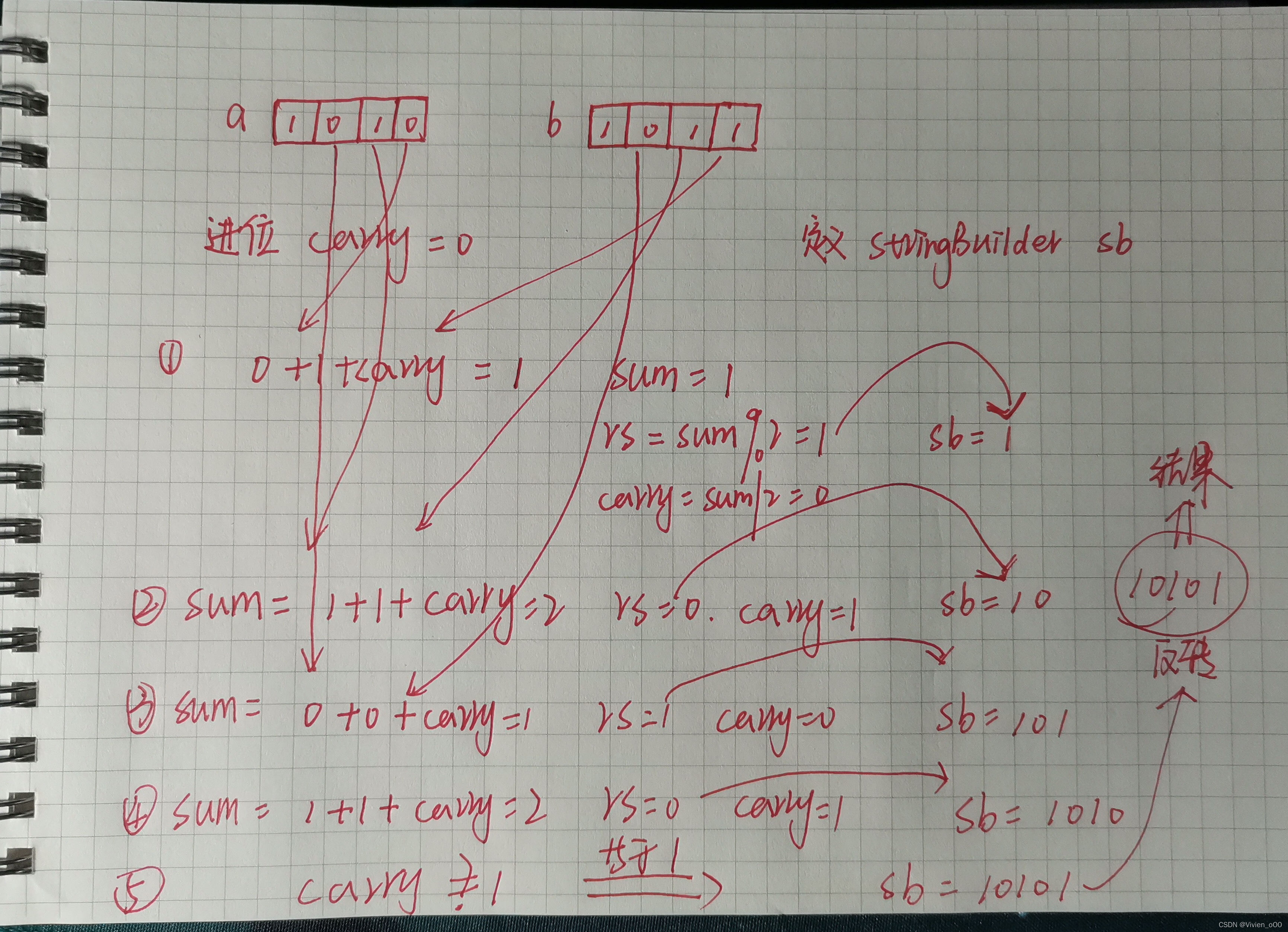
看上图:
很明显我们直到,二进制运算对2取余就是当前位,除于2就是进位。
比如: 0+0=0;进位为0,当前位为0;
0+1=1;进位位0,当前位为1;
1+1=10;进位为1,当前位为0;
从后往前运算,每次从a和b各取一个数字和进位相加;每次得到的当前位的结果,拼接起来,进位放在下一位运算。
ans.append(sum % 2);
//除二为进位
ca = sum / 2;
如果一个字符串已经运算完,另一个还没有运算完,就将已经运算玩的哪的二进制设位0,进行运算,
//i>0 代表a没遍历完,就让a等于它本来的值,否则就等于0
sum += i >= 0 ? a.charAt(i) - '0' : 0;
sum += j >= 0 ? b.charAt(j) - '0' : 0;
最后当两个都遍历完,如果进位位1,就将其拼接起来。最后将所拼接的字符串反转就是我们所得的结果。
代码:
public static String addBinary2(String a, String b) {
//定义一个StringBuilder用来拼接结果
StringBuilder ans = new StringBuilder();
//初始化进位为0,
int ca = 0;
//直到两个字符串都遍历完为止
for (int i = a.length() - 1, j = b.length() - 1; i >= 0 || j >= 0; i--, j--) {
//sum = ca + a + b
int sum = ca;
//i>0 代表a没遍历完,就让a等于它本来的值,否则就等于0
sum += i >= 0 ? a.charAt(i) - '0' : 0;
sum += j >= 0 ? b.charAt(j) - '0' : 0;
//结果是对二取余数
ans.append(sum % 2);
//除二为进位
ca = sum / 2;
}
//遍历完如果进位为1,就将一加到后面
ans.append(ca == 1 ? ca : "");
//最后对字符串进行反转
return ans.reverse().toString();
}
位运算
首先我们先说一下:
位运算加法是用异或 ^:
相同为0,不同为1
0 ^ 0 结果为0
0 ^ 1 结果为1
1 ^ 1 结果为0,因为进位了
进位用and也就是与运算&
只有同时为1是才为1
0 & 0 结果为0
0 & 1 结果为0
1 & 1 结果为1
首先看图解:


首先初始化一个字符数组,长度为a和b最长的那个+1,因为有可能会有进位。将这和字符数组初始化为全‘0’数组
char[] rs = new char[Math.max(a.length(), b.length()) + 1];
//将其初始化位0
for (int i = 0; i < rs.length; i++) {
rs[i] = '0';
}
定义两个数组max,min,分别存两个字符串。
char[] max = (a.length() >= b.length() ? a : b).toCharArray();
char[] min = (a.length() >= b.length() ? b : a).toCharArray();
将短的那个赋值给我们定义字符数组
//将短的赋给rs
for (int i = 0; i < min.length; i++) {
rs[rs.length - 1 - i] = min[min.length - 1 - i];
}
然后max和re从后往前逐位进行运算
int carry = 0;
//诸位进行运算
for (int i = 0; i < max.length; i++) {
int left = rs[rs.length - 1 - i] == '0' ? 0 : 1;
int right = max[max.length - 1 - i] == '0' ? 0 : 1;
int v = left ^ right ^ carry;
carry = (left & right) + ((left ^ right) & carry);
rs[rs.length - 1 - i] = v > 0 ? '1' : '0';
}
最后将carry放在第一位即可
//进位大于一 就加个一
if (carry > 0) {
rs[0] = '1';
return new String(rs);
} else {
rs[0] = ' ';
return new String(rs).trim();
}
最后关于其中位运算代码,在作以解释
int v = left ^ right ^ carry;
异或可以进行多位运算,等同于加法。
可以计算作为验证
carry = (left & right) + ((left ^ right) & carry);
计算进位
对于left & right和(left ^ right) & carry
他们两个的结果不可能同时为1,大家可以自己运算。
我们讲讲为什么要这么算进位
当不算进位,两个数都为0的时候,不论进位值为几,这几个数相加都不可能产生进位。left & right和(left ^ right)都为0,所以与carry无关。
当两个同时为1时一定产生进位,左边已经为1,但(left ^ right)为0,与进位无关。所以最后的进位结果是1;
当两个数一个为0一个为1时,加号左边为0,(left ^ right)为1,此时与carry有关,当carry为1,时会产生进位,当carry为0时不产生进位,所以时&carry。
完整代码:
//初始话一个最大长度+1的字符数组,因为最后可能产生进位,所以加一
char[] rs = new char[Math.max(a.length(), b.length()) + 1];
//将其初始化位0
for (int i = 0; i < rs.length; i++) {
rs[i] = '0';
}
//max等于长的字符串,min等于短的字符串
char[] max = (a.length() >= b.length() ? a : b).toCharArray();
char[] min = (a.length() >= b.length() ? b : a).toCharArray();
//将短的赋给rs
for (int i = 0; i < min.length; i++) {
rs[rs.length - 1 - i] = min[min.length - 1 - i];
}
int carry = 0;
//诸位进行运算
for (int i = 0; i < max.length; i++) {
int left = rs[rs.length - 1 - i] == '0' ? 0 : 1;
int right = max[max.length - 1 - i] == '0' ? 0 : 1;
int v = left ^ right ^ carry;
carry = (left & right) + ((left ^ right) & carry);
rs[rs.length - 1 - i] = v > 0 ? '1' : '0';
}
//进位大于一 就加个一
if (carry > 0) {
rs[0] = '1';
return new String(rs);
} else {
rs[0] = ' ';
return new String(rs).trim();
}