[数据结构与算法]数据结构（图+部分算法）

图

图是一种数据结构，其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。 结点也可以称为顶点。

邻接矩阵

邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是的row和col表示的是1…n个点。

邻接表

1)邻接矩阵需要为每个顶点都分配n个边的空间，其实有很多边都是不存在,会造成空间的一定损失.

2)邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成

基本用法

package graph;

import java.util.ArrayList;
import java.util.Arrays;

public class Graph {

    private ArrayList<String>vertexList;//存储顶点集合
    private int[][]edges;//存储图对应的邻接矩阵
    private int numOfEdges;//表示边的数目

    //构造器
    public Graph(int n){
        //初始化矩阵和vertexList
        edges=new int[n][n];
        vertexList=new ArrayList<String>(n);
        numOfEdges=0;
    }

    //图中常用的方法
    //返回结点的个数
    public int getNumOfVertex(){
        return vertexList.size();
    }
    //得到边的数目
    public int getNumOfEdges(){
        return numOfEdges;
    }
    //返回结点i(下标)对应的数据
    public String getValueByIndex(int i){
        return vertexList.get(i);
    }

    //返回v1和v2的权值
    public int getWeight(int v1,int v2){
        return edges[v1][v2];
    }

    //显示图对应的矩阵
    public void showGraph(){
        for(int[]link:edges){
            System.out.println(Arrays.toString(link));
        }
    }


    //插入结点
    public void insertVertex(String vertex){
        vertexList.add(vertex);
    }

    //添加边

    /**
     *
     * @param v1 表示点的下标即第几个顶点
     * @param v2
     * @param weight
     */
    public void insertEdge(int v1,int v2,int weight){
        edges[v1][v2]=weight;
        edges[v2][v1]=weight;
        numOfEdges++;
    }

    public static void main(String[] args) {

        int n=5;
        String[] vertexValue ={"A","B","C","D","E"};

        Graph graph = new Graph(n);

        for(String value:vertexValue){
            graph.insertVertex(value);
        }

        //添加边
        graph.insertEdge(0,1,1);
        graph.insertEdge(0,2,1);
        graph.insertEdge(1,2,1);

        graph.showGraph();

    }
}

图的遍历

深度优先

深度优先遍历基本思想

图的深度优先搜索(Depth First Search) 。

1)深度优先遍历，从初始访问结点出发，初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点， 可以这样理解：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。

2)我们可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。

3)显然，深度优先搜索是一个递归的过程

深度优先遍历算法步骤

1)访问初始结点v，并标记结点v为已访问。

2)查找结点v的第一个邻接结点w。

3)若w存在，则继续执行4，如果w不存在，则回到第1步，将从v的下一个结点继续。

4)若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。

5)查找结点v的w邻接结点的下一个邻接结点，转到步骤3。

    //定义一个数组boolean[]，记录某个结点是否被访问过
    private boolean [] isVisited;

    //构造器
    public Graph(int n){
        //初始化矩阵和vertexList
        edges=new int[n][n];
        vertexList=new ArrayList<String>(n);
        numOfEdges=0;
        isVisited=new boolean[n];
    }

    //得到第一个邻接结点的下标w
    public int getFirstNeighbor(int index){
        for(int j=0;j<vertexList.size();j++){
            if(edges[index][j]>0){
                return j;
            }
        }
        return -1;
    }

    //根据前一个邻接结点的下标来获取下一个邻接结点
    public int getNextNeighbor(int v1,int v2){
        for(int j=v2+1;j<vertexList.size();j++){
            if(edges[v1][j]>0){
                return j;
            }
        }
        return -1;
    }

    //深度优先的遍历算法
    //i 第一次就是 0
    private void dfs(boolean[]isVisited,int i){
        //首先我们访问结点，输出
        System.out.print(getValueByIndex(i)+"->");
        //将给结点设置为已经访问
        isVisited[i]=true;
        //查找结点i的第一个邻接结点w
        int w=getFirstNeighbor(i);
        while(w!=-1){//说明有
            if(!isVisited[w]){
                dfs(isVisited,w);
            }
            //如果w结点已经被访问过
            w=getNextNeighbor(i,w);
        }
    }

    //对dfs 进行一个重载，遍历我们所有的结点，并进行dfs
    public void dfs(){
        //遍历所有的结点，进行dfs[回溯]
        for (int i = 0; i < getNumOfVertex(); i++) {
            if(!isVisited[i]){
                dfs(isVisited,i);
            }
        }
    }

广度优先

广度优先遍历基本思想

图的广度优先搜(Broad First Search) 。

类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点

广度优先遍历算法步骤

1)访问初始结点v并标记结点v为已访问。

2)结点v入队列

3)当队列非空时，继续执行，否则算法结束。

4)出队列，取得队头结点u。

5)查找结点u的第一个邻接结点w。

6)若结点u的邻接结点w不存在，则转到步骤3；否则循环执行以下三个步骤：

6.1 若结点w尚未被访问，则访问结点w并标记为已访问。

6.2 结点w入队列

6.3 查找结点u的继w邻接结点后的下一个邻接结点w，转到步骤6。

//对一个结点进行广度优先遍历的方法

    private void bfs(boolean[] isVisited,int i){
        int u;//表示队列的头结点对应的下标
        int w;//邻接结点w
        //队列，结点访问的顺序
        LinkedList<Integer> queue = new LinkedList<>();
        //访问结点，输出结点信息
        System.out.print(getValueByIndex(i)+"=>");
        //标记为以访问
        isVisited[i]=true;
        //将结点加入队列
        queue.addLast(i);

        while(!queue.isEmpty()){
            //取出队列的头结点
            u=queue.removeFirst();
            //得到第一个邻接结点的下标w
            w=getFirstNeighbor(u);
            while(w!=-1){//找到
                //是否访问过
                if(!isVisited[w]){
                    System.out.print(getValueByIndex(w)+"=>");
                    //标记已经访问
                    isVisited[w]=true;
                    //入队
                    queue.addLast(w);
                }

                //以u前驱结点，找w后面的下一个邻接结点
                w=getNextNeighbor(u,w);//体现出广度优先
            }
        }

    }

    //遍历所有结点，都进行广度优先
    public void bfs(){
        for (int i = 0; i < getNumOfVertex(); i++) {
            if(!isVisited[i]){
                bfs(isVisited,i);
            }
        }
    }

二分查找（非递归）

package binarySearch;

public class BinarySearch {
    public static void main(String[] args) {

        int[] arr = new int[]{1, 3, 8, 10, 11, 67, 100};
        int i = binarySearch(arr, 10);
        System.out.println(i);

        int i1 = binarySearch(0, arr.length, 10, arr);
        System.out.println(i1);

    }

    /**
     * @param arr    待查找的数组，arr是升序排序
     * @param target 需要查找的数
     * @return 返回对应的下标，-1 表示没找到
     */
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {//说明继续查找
            int mid = (left + right) / 2;
            if (arr[mid] == target) {
                return mid;
            } else if (arr[mid] > target) {
                right = mid - 1;//需要向左边查找
            } else {
                left = mid + 1;//需要向右边查找
            }
        }
        return -1;
    }

    public static int binarySearch(int left, int right, int target, int[] arr) {
        int mid = (left + right) / 2;
        if (left > right) return -1;
        if(arr[mid]==target)return mid;

        if (arr[mid] > target)
            return binarySearch(mid + 1, right, target, arr);
        else
            return binarySearch(left, mid - 1, target, arr);
    }

}

分治算法

分治(Divide-and-Conquer§)算法设计模式如下：

if |P|≤n0

  then return(ADHOC(P))

//将P分解为较小的子问题 P1 ,P2 ,…,Pk

for i←1 to k

do yi ← Divide-and-Conquer(Pi)  递归解决Pi

T ← MERGE(y1,y2,…,yk)  合并子问题

return(T)

其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。ADHOC§是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC§求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法，用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。

分治算法的最佳实现——汉诺塔

package dac;

public class HanoiTower {
    public static void main(String[] args) {
        hanoiTower(5,'A','B','C');
    }

    //汉诺塔的移动方法
    //使用分治算法
    public static void hanoiTower(int num,char a,char b,char c){
        //如果只有一个盘
        if(num==1){
            System.out.println("第一个盘从 "+a+"->"+c);
        }else{
            //如果我们有n>=2情况，我们总是可以看作是两个盘 1、最下面的一个盘2、上面的所有盘
            //1、先把 最上面的所有盘A->B，移动过程中会使用到c
            hanoiTower(num-1,a,c,b);
            //2、把最下边的盘A->C
            System.out.println("第"+num+"个盘从 "+a+"->"+c);
            //3、把B塔的所有盘 从B->C ,移动过程会使用到a塔
            hanoiTower(num-1,b,a,c);
        }
    }


}

动态规划

动态规划算法介绍

1)动态规划(Dynamic Programming)算法的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法

2)动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

3)与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )

4)动态规划可以通过填表的方式来逐步推进，得到最优解.

最佳实践——背包问题

package dynamic;

public class KnapsackProblem {
    public static void main(String[] args) {
        int[]w={1,4,3};//物品的重量
        int[]val={1500,3000,2000};//物品的价值

        int m=4;//背包的容量
        int n=val.length;//物品的个数

        //创建二维数组
        //v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
        int [][]v=new int[n+1][m+1];
        //为了记录放入商品的情况，定义一个二维数组
        int [][]path =new int[n+1][m+1];

        //初始化第一行和第一列，这里在本程序中，可以不去处理，因为默认就是0
        for (int i = 0; i < v.length; i++) {
            v[i][0]=0;//将第一列设置为0
        }
        for (int i = 0; i < v[0].length; i++) {
            v[0][i]=0;//将第一行设置为0
        }

        //更据得到的公式来动态规划处理
        for (int i = 1; i < v.length; i++) {//不处理第一行 ，i是从1开始
            for(int j=1;j<v[0].length;j++){//不处理第一列 j是从1开始
                if(w[i-1]>j){
                    v[i][j]=v[i-1][j];
                }else{
                    //v[i][j]=Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);
                    if(v[i-1][j]<val[i-1]+v[i-1][j-w[i-1]]){
                        v[i][j]=val[i-1]+v[i-1][j-w[i-1]];
                        //把当前的情况记录到path
                        path[i][j]=1;
                    }else{
                        v[i][j]=v[i-1][j];
                    }
                }
            }
        }

        //输出一下v 看看目前的情况
        for (int i = 0; i < v.length; i++) {
            for (int j=0;j<v[i].length;j++){
                System.out.print(v[i][j]+" ");
            }
            System.out.println();
        }

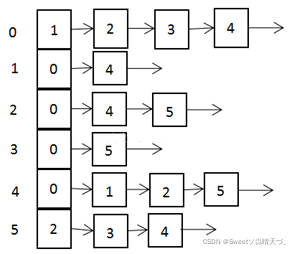
        System.out.println("======================");
        //输出最后放入的哪些商品

        int i=path.length-1;
        int j=path[0].length-1;
        while(i>0&&j>0){//从path的最后开始找
            if(path[i][j]==1){
                System.out.println("第"+i+"个商品放入到背包");
                j-=w[i-1];
            }
            i--;
        }
    }
}