本来这一题不在我的做题范围内的,但是上一篇文章有位朋友留言问我能不能做一下这一题,然后打开看了一下, 噢?简单题? 那做一下吧,结果掉进坑里了…
1. 题目描述
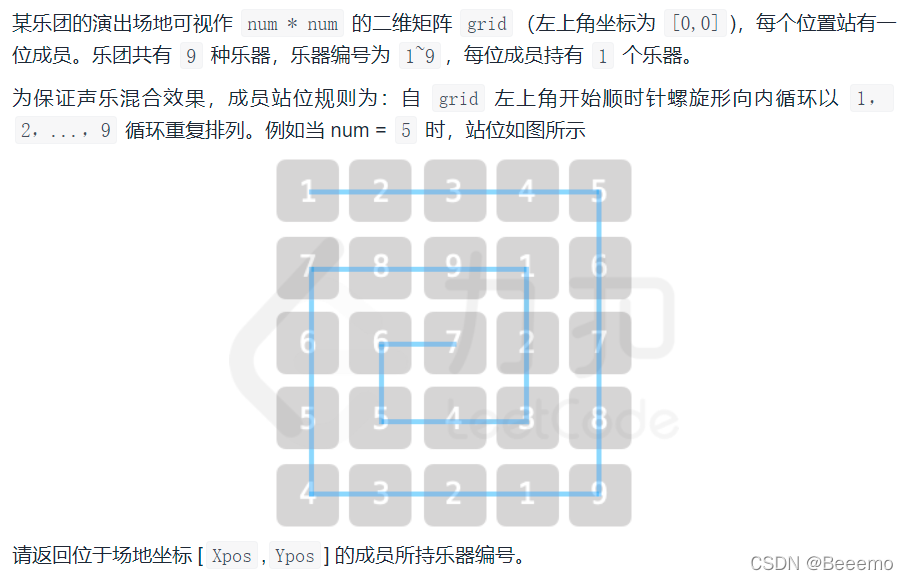

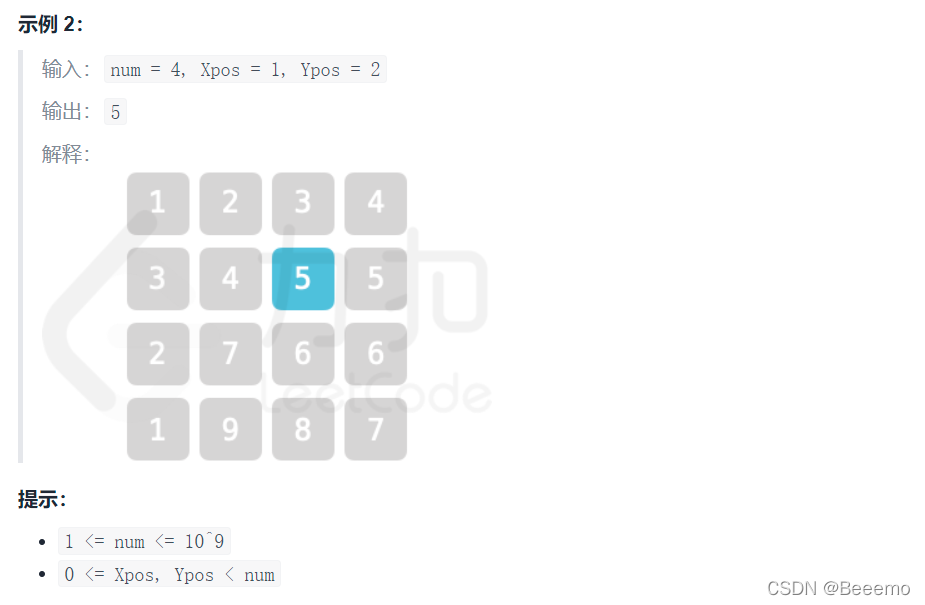
2. 解题思路
既然这是一个num*num的矩阵,而且数字是顺时针按1-9递增的,那么就可以顺时针依次剥掉一层“外皮”,从num*num的矩阵变成(num-1)*(num-1)的矩阵,如下图所示:
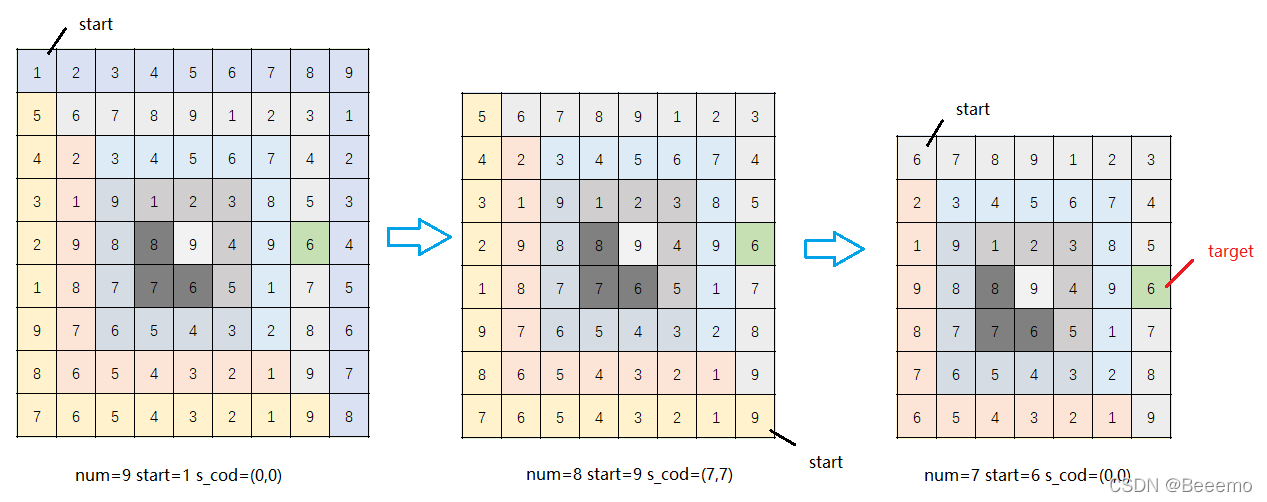
每一种颜色为一层 “外皮”,依次剥掉的 “外皮”,每剥掉一次则重新计算起始方块中的坐标和数值与目标方块的坐标,通过目标方块的坐标与起始方块的坐标判断是否在本层中,是则可以通过起始方块的数值计算目标方块的数值。显然,在这种逻辑下,递归是一个解决方案之一。然而一提交,我还是太年轻了,怎么想得到他的乐团居然能有971131546*971131546那么多人呢?结果就是栈溢出,无法求解
看来递归是不行了,得另谋出路。究竟怎么样才可以快速剥掉若干层“外皮” 到达目标位置那一层呢?想了很久还是找不出别的解决方法,于是只能看看大神们的思路怎么样。一看大佬们的思路茅塞顿开,它被命名为求面积之差,那就可以知道起始点与目标层起点之间间隔了多少个位置从而推算出目标层起点的数值,语言显然有点苍白无力,还是来看个图吧:
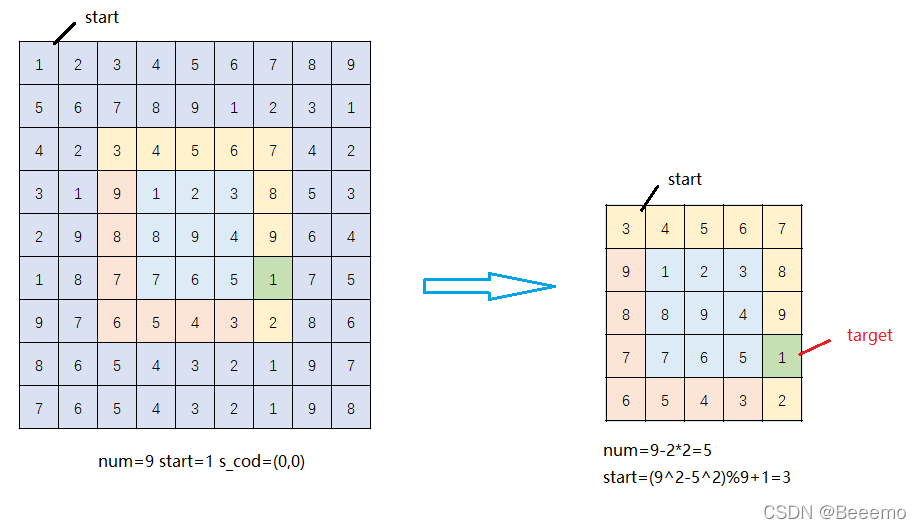
这个过程应该一眼就能看懂了,就不过多解释了,剩下的步骤依然是用前面递归的想法进行实现。
当这个算法提交正确之后,我就在想,可以把递归改成非递归试一下,说不定会减少内存占用呢?毕竟递归一次后栈里面就多一个东西。兴致勃勃地把他改成了非递归实现,一验证?咦怎么结果还有负数的?可是我逻辑是正确的呀?百思不得其解打印过程变量看了一眼,好家伙,int不够用溢出了,马上改为了long,这下子终于正常运行了,没什么好多说的了,有兴趣就看看下面的代码吧。
3. 代码实现
3.1 逐层递归(卒 | 栈溢出)
public int orchestraLayout(int num, int xPos, int yPos) {
int iter = 0;
int start = 1;
return digui(iter, num, xPos, yPos, start);
}
public int digui(int iter, int num, int xPos, int yPos, int strat) {
if (iter % 2 == 0) {
if (xPos == 0)
return (strat + yPos - 1) % 9 + 1;
else if (yPos == num - 1)
return (strat + num + xPos - 2) % 9 + 1;
else
xPos--;
} else {
if (xPos == num - 1)
return (strat + num - yPos - 2) % 9 + 1;
else if (yPos == 0)
return (strat + num + num - xPos - 3) % 9 + 1;
else
yPos--;
}
strat = (strat + num * 2 - 2) % 9 + 1;
return digui(++iter, --num, xPos, yPos, strat);
}
3.2 去除外层再递归
public int orchestraLayout(int num, int xPos, int yPos) {
int round = Math.min(Math.min(xPos, num - 1 - xPos), Math.min(yPos, num - 1 - yPos));
int start = (int) (((long) num * num - (long) (num - round * 2) * (num - round * 2)) % 9 + 1);
return digui(0, num - round * 2, xPos - round, yPos - round, start);
}
public int digui(int iter, int num, int xPos, int yPos, int strat) {
System.out.println("iter:" + iter + ", num:" + num + ", xPos:" + xPos + ", yPos:" + yPos + ", strat:" + strat);
if (iter % 2 == 0) {
if (xPos == 0)
return (strat + yPos - 1) % 9 + 1;
else if (yPos == num - 1)
return (strat + num + xPos - 2) % 9 + 1;
else
xPos--;
} else {
if (xPos == num - 1)
return (strat + num - yPos - 2) % 9 + 1;
else if (yPos == 0)
return (strat + num + num - xPos - 3) % 9 + 1;
else
yPos--;
}
strat = (strat + num * 2 - 2) % 9 + 1;
return digui(++iter, --num, xPos, yPos, strat);
}
这是本题我所提交的代码中的最优表现(好像还是刷LeetCode的第一次双百)

3.3 去除外层直接求解
public int orchestraLayout(int num, int xPos, int yPos) {
int round = Math.min(Math.min(xPos, num - 1 - xPos), Math.min(yPos, num - 1 - yPos));
int start = (int) (((long) num * num - (long) (num - round * 2) * (num - round * 2)) % 9 + 1);
num = num - round * 2;
xPos = xPos - round;
yPos = yPos - round;
if (xPos == 0)
return (start + yPos - 1) % 9 + 1;
else if (yPos == num - 1)
return (int) ((start + (long) num + xPos - 2) % 9 + 1);
else if (xPos == num - 1)
return (int) ((start + (long) num * 3 - yPos - 4) % 9 + 1);
else
return (int) ((start + (long) num * 4 - xPos - 5) % 9 + 1);
}
虽然代码看起来很简洁,非递归,然而却不是最优解。

3.4 对比
看完结果是不是有点震惊?非递归居然比递归所占用的内存还要多?一开始我也是有这样的疑惑,认真想了一下之后发现也有道理。因为在递归时候,虽然是栈内存中会多一个递归函数,但计算相对数值不大,只需要使用int变量即可;而在改成了非递归之后,虽然是少了个栈内存,但由于计算没有递归便捷,计算过程容易超出int范围而必须使用long,众所周知long所占的空间是比int大的,这应该也是造成本次差异的重要原因。

最后再来吐槽一句,这真的是简单题吗??????