概念定义
1.1 等差数列
??等差数列是指任意两个相邻的数的差是相等的,这个差值被称为公差,我们在数学中通常用d表示,a?作为首项。
ai的递推公式如下:
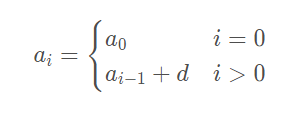
1.2 等比数列
??等比数列是指任意两个相邻的数之间的差是相等的,我们在数学中用q表示公共比,a?为首项。
ai的递推公式如下:
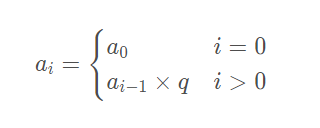
1.3 斐波那契数列
??斐波那契数列是一个除第0项和第一项外,后面的数都由其前面两个数之和组成,公式如下:
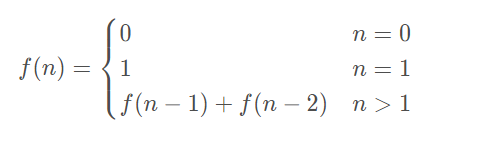
斐波那契数列在对递归的理解有着至关重要的作用,同时它也是一道经典的动态规划问题。
二. 推荐专栏
三. 相关练习
3.1 斐波那契数
对于斐波那契数列,我们要想直到该数列中的某个值,那我们得需直到其前面的两个值,即公式f(n) = f(n - 1) + f(n - 2),所以我们可以用递归的方式进行计算。
例如我们要计算f(4),那我们首先要知道f(3)和f(2),要知道f(3)和f(2)我们首先要知道f(1) 和f(0),题目中给出我们f(0) = 0, f(1) = 1。那我们可以重复调用一个函数,每次调用都n-1,当n = 0或n = 1时返回0或1。
代码如下:
int fib(int n){
//如果n == 0,因为我们f(0) = 0,则直接返回0
if(n == 0){
return 0;
}
//同理返回
if(n == 1 || n == 2){
return 1;
}
//当n > 1时,我们需要知道其前面的两个数列值,分别调用fib(n - 1)和fib(n - 2)
return fib(n - 1) + fib(n - 2);
}
3.2 第 N 个泰波那契数
这道题和上道题没有太大的区别,只是将公式改为 Tn+3 = Tn + Tn+1 + Tn+2,这次我们用循环的方式来解决,循环的话我们只需从i = 3开始,同时用三个变量分别记录i - 1,i - 2,i - 3,以保证我们能够得到i
代码如下:
int tribonacci(int n){
int t0 = 0, t1 = 1, t2 = 1;
int num = 0;
if(n == 0)return 0;
if(n == 1 || n == 2)return 1;
for(int i = 3; i <= n; i++){
num = t0 + t1 + t2;
t0 = t1;
t1 = t2;
t2 = num;
}
return num;
}
3.3 单调数列
这道题我们首先要判断其为递增,还是递减,如何在判断是否单调
代码如下:
bool isMonotonic(int* nums, int numsSize){
if(numsSize <= 2){
return true;
}
int flag, i;
//判断增序还是降序
for(i = 1; i < numsSize; i++){
if(nums[i] > nums[i - 1]){
flag = 1;
break;
}
else if(nums[i] < nums[i - 1]){
flag = -1;
break;
}
if(nums[i] == nums[i - 1])flag = 0;
}
if(!flag)return true;
//判断是否单调
for(int i = 2; i < numsSize; i++){
if(flag == 1 && nums[i] < nums[i - 1]){
return false;
}
if(flag == -1 && nums[i] > nums[i - 1]){
return false;
}
}
return true;
}