数据结构笔记总结(到线性表结束)
数据结构绪论
逻辑结构与物理结构
逻辑结构
逻辑结构:是指数据对象中数据元素之间的相互关系面向问题的。
逻辑结构可以分为四类。
集合结构
即数据除了在同一集合中无其他关系。
线性结构
数据元素之间是一对一关系
树形结构
数据元素之间呈现一对多关系
图形结构
数据元素之间呈现多对多关系
物理结构
线性存储
数据均放在连续的存储空间中。可以进行随机访问。链式存储
链式存储
把数据存储在任意存储单元,各个数据的关系通过指针来表示
算法
概念
说白了就是解决问题办法
特性
基本的输入输出
有穷性
指算法在执行有限的步骤之后,自动结束而不会出现无线循环,并且每一个步骤在可接受范围内完成
确定性
算法每一步都具有确定的定义,不能同一种情况进入不同的分支
可行性
算法的每一步都必须可行
设计要求
正确性
算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性,能正确反应问题的需求、能够的到问题的正确答案
本人翻译:就是算法算出来的必须是对的
健壮性
当输入数据不合法时,算法也能做出相关处理,而不是产生异常或莫名奇妙的结果
本人翻译:就是当用户点一份蛋炒饭时程序不会炸
可读性
算法设计的另一目的是为了便于月的、理解和交流
本人翻译:说白了就是要让人能看懂
时间效率高和存储量低
本人翻译:跑程序时电脑不卡,跑的快,又不占内存
算法优劣的判断方法
时间复杂度
时间复杂度所需消耗的时间即基本操作执行次数
时间复杂度的计算
该方法就是大O阶表示法的计算方法
(1)用常数 1取代运行时间中的所有加法常数
(2)在修改后的运行次数函数中,只保留最高阶项
(3)如果最高阶项存在且不是 1,则去除与这个项相乘的常数
常用时间复杂度的比较
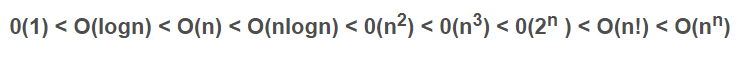
空间复杂度
运行完一个程序所需内存的大小
注:感觉用得不多,目前了解定义就行
线性表
定义
零个或多个数据元素的有限序列
线性表的顺序存储结构
定义
用一段连续得存储空间对数据进行存储
本人翻译:说白了就是数组
特性
拥有随机访问特性
时间复杂度
(1)对于存取操作
线性表的顺序存储结构,对于存取操作,其时间复杂度为O(1)
因为元素位置可以直接计算得到
(2)对于插入和删除操作
对于插入和删除操作,其时间复杂度为O(n)因为插入或删除后,需要移动其余元素
使用场景
因此,线性表顺序存储结构比较适用于元素存取操作较多,增删操作较少的场景
线性表的链式存储结构
定义
一个或多个结点组合而成的数据结构称为链表
节点
节点一般由两部分组成
数据域
用来装需要存储的数据
指针域
存储指向下一个节点的指针
头节点
为了能更加方便地对链表进行操作,会在单链表的第一个结点(即头指针)前附设一个结点,称为 头结点
该节点不装任何实际数据方便操作
注:并非每个链表都有
头指针
指向第一个节点的指针称之为头指针
注:不一定是头指针
单链表
单链表的时间复杂度
(1)存取操作
而对于单链表结构,假设需要获取第 i 个元素,则必须从第一个结点开始依次进行遍历,直到达到第 i 个结点。因此,对于单链表结构而言,其数据元素读取的时间复杂度为O(n)
注:你需要从第一个开始一个一个去找,而不是通过下标一下子找到,所以时间复杂度为O(n)
(2)插入删除
对其任意一个位置进行增删操作,其时间复杂度为O(n)
注:之所以还为O(n)主要原因是你需要找到所需插入的元素
链式表与顺序表的优缺点
缺点
链式表存取操作的时间复杂度更高
优点
虽然插入删除两种时间复杂度都为都为O(n),但是如果需要插入删除,顺序表由于每次插入删除都要移动其他元素,所以每次都为O(n),而链式表第一次插入时查找到所需要的位置,之后的插入删除操作仅需要修改一下指针,所以之后的插入删除操作的时间复杂度为O(1)
链式表与顺序表的选择
经常进行存取操作时,可选择顺序表
经常进行插删操作时,可选择链式表
循环链表
定义
将单链表中的终端结点的指针端由空指针改为指向头结点就使整个单链表形成一个环这种头尾相接的单链表称为单循环链表,简称 循环链表
个人翻译:就是把链表最后的节点的下一个节点指向第一个节点
注:头节点的作用是判断首尾,并非每一个循环链表都需要头节点
作用
循环链表要好使用需要设置一个尾指针指向循环链表的最后一个节点,这样便可以使寻找尾节点的时间复杂度调为O(1),并且寻找头节点也只需要移动到下一个或下下个节点,时间复杂度也为O(1)
双向链表
定义
在单链表的每个结点中,再设置一个指向其前驱结点的指针域
双向循环链表
既然单链表有循环链表,那双向链表自然有双向循环链表
双向循环链表重点
双向循环链表最重要的是在插入删除时的操作顺序
插入时:
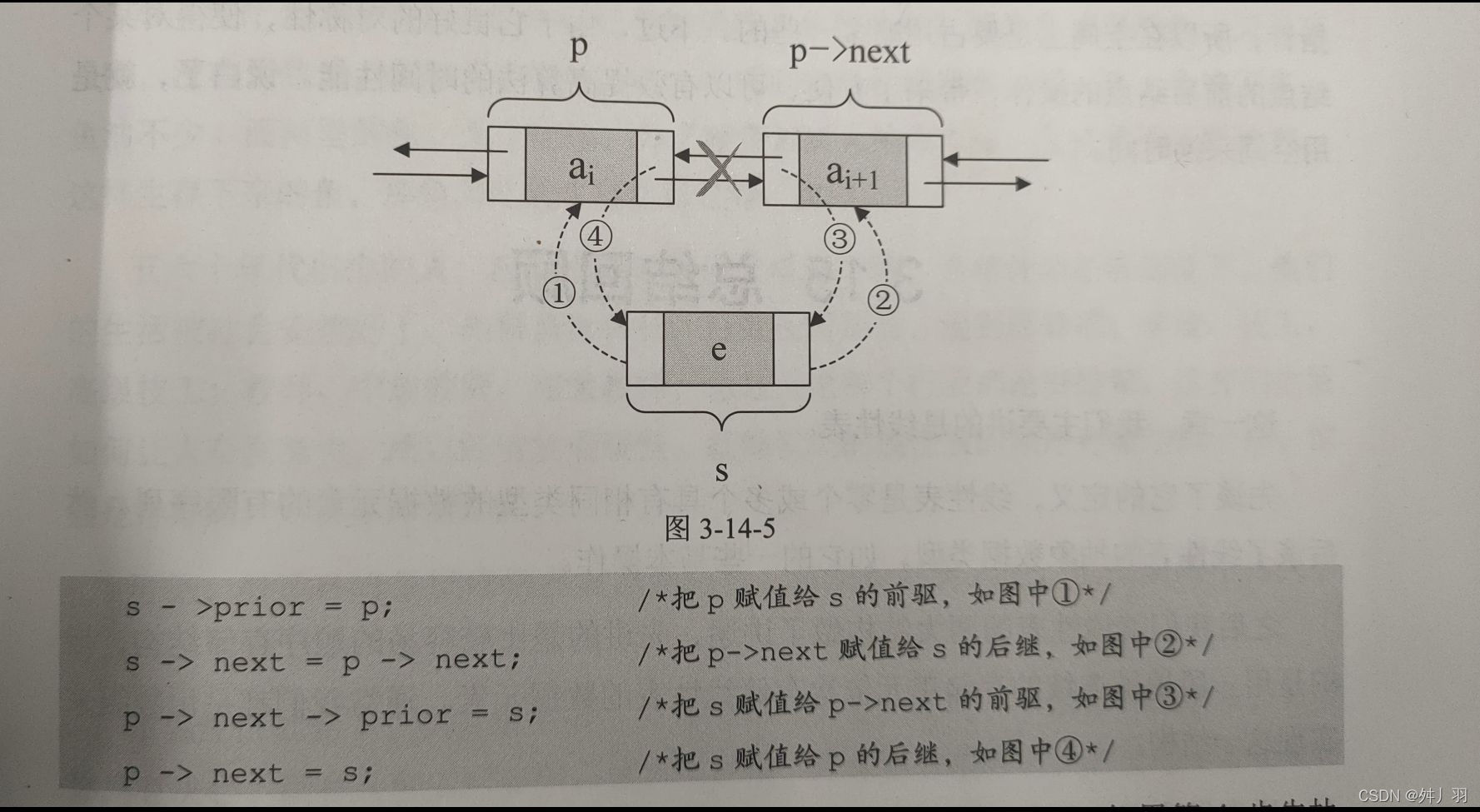
删除时:
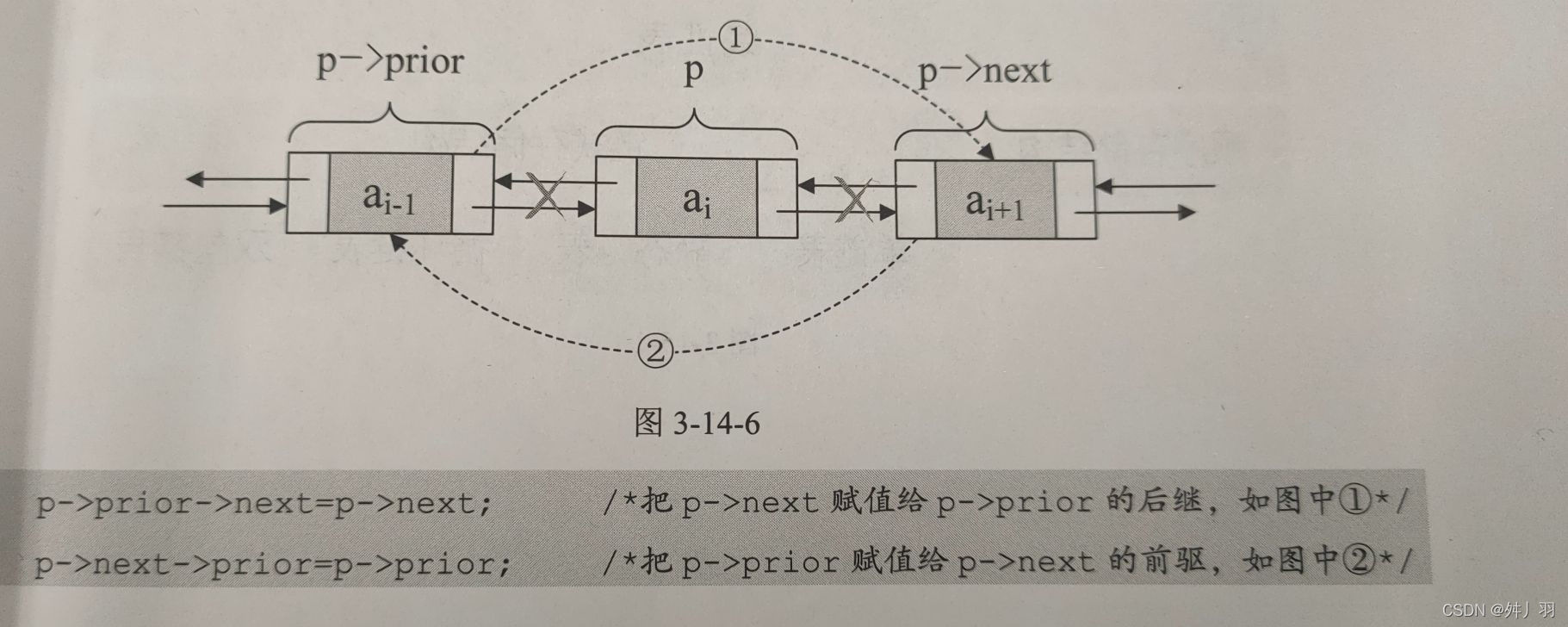
删除时记得要将删除的节点释放