算法设计与分析基础(七):分治法
-
基本思想
将规模为 N 的问题分解为 k 个规模较小的子问题,使得这些子问题相互独立并可分别求解, 再将 k 个子问题的解“合并”成原问题的解. 如子问题的规模仍很大, 则反复分解直到问题小到可直接求解为止。
在分治法中, 子问题的解法通常与原问题相同,自然导致递归过程。 -
特点
- 算法适宜并行计算
- 算法的计算复杂度对应如下递归方程
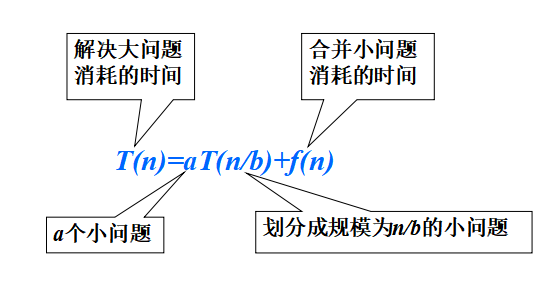
预备知识
T(n)=aT(n/b)+f(n)递推式的解法
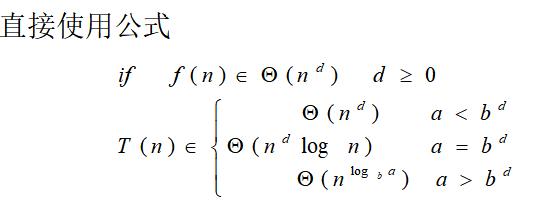
合并排序
- 问题:将n个元素排成非递减顺序。
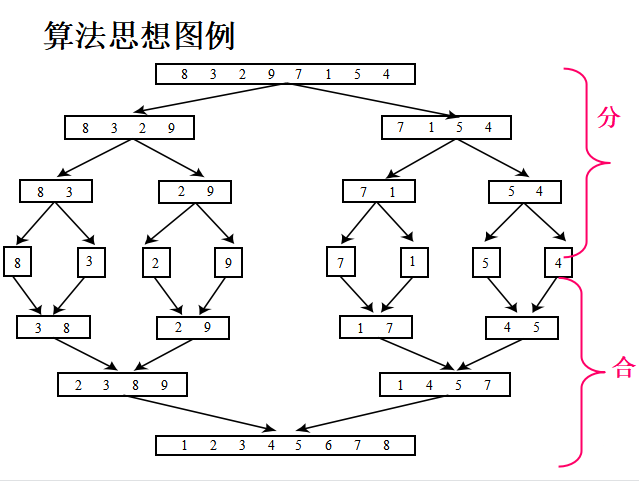
- 算法思想
- 若n为1, 算法终止; 否则,
- 将n个待排元素分割成k (k=2) 个大致相等子集合A、B,
- 对每一个子集合分别递归排序,
- 再将排好序的子集归并为一个集合。
-
伪代码
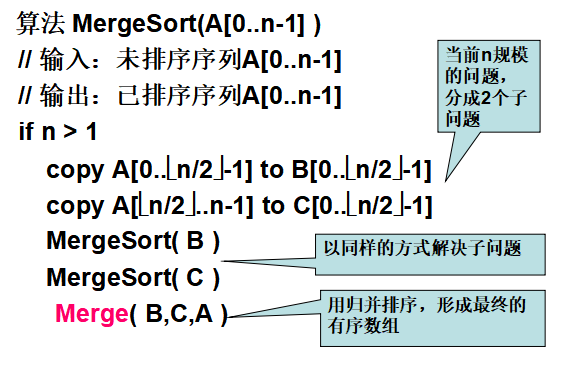
Merge(B,C,A):

-
结论

缺点:需要线性的额外空间。
? 虽然合并也可以做到“在位”,但导致算法过程过于复杂。
快速排序
算法思路:对于输入A[0… n-1],按以下三个步骤进行排序:
-
元素划分
取A中的一个元素为支点(pivot), 将A[0…n-1]划分成3段: A[0…s-1], A[s ], A[s+1…n-1], 使得
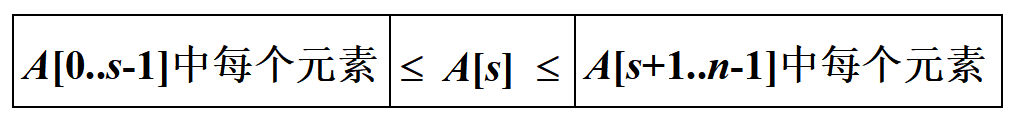
下标s在划分过程中确定。
-
递归排序
递归调用快速排序法 分别对A[0…s-1]和A[s+1…n-1]排序。
-
有序段串接
将已经有序的 A[0…s-1], A[s], A[s+1…n-1] “连接”成 整体有序的A[0…n-1]。
分区的例子(双向扫描)
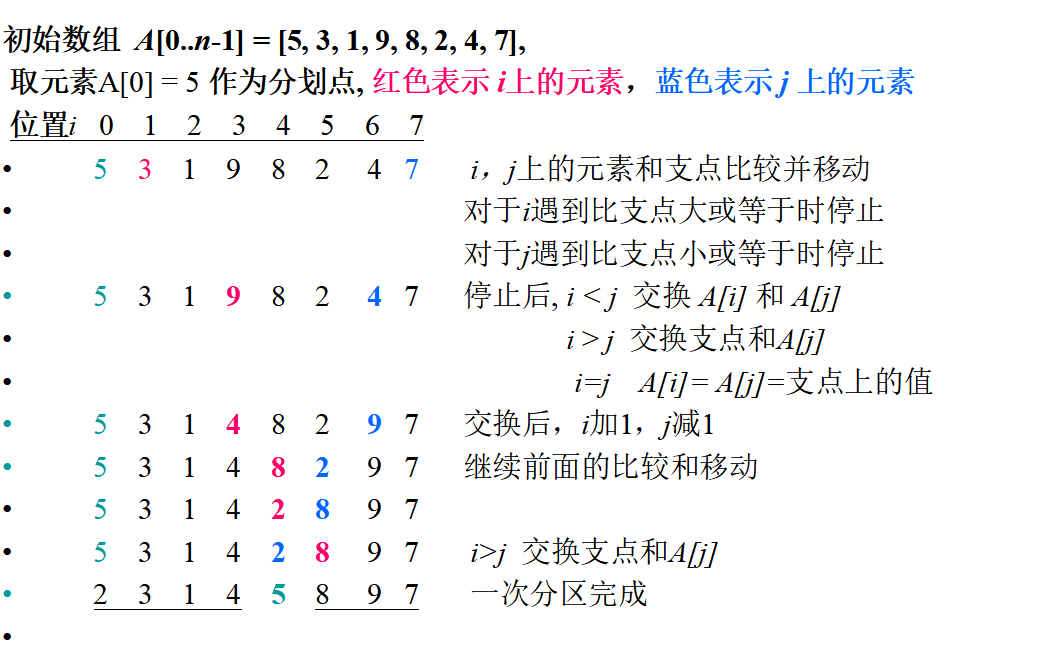
伪代码
算法 Partition( A[l..r] )
// 输入:子数组A[l..r]
// 输出:分划点/基准点pivot的位置
begin p ← A[l]; i ← l; j ← r+1;
repeat
repeat i ←i + 1 until A[i] ≥ p ;
repeat j ← j – 1 until A[j] ≤ p ;
swap ( A[i], A[j] )
until i ≥ j ;
swap ( A[i], A[j] );
swap ( A[l], A[j] );
return j;
end
快速排序
If l < r
s ← Partition( A[l..r] )
QuickSort( A[l..s-1] )
QuickSort( A[s+1..r] )
算法复杂度满足以下方程:
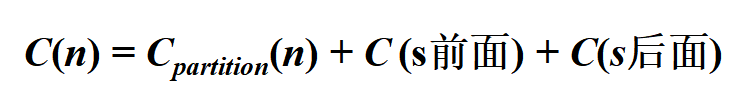
上式依赖于s的位置。partition的基本操作:比较
Partition的最坏情况:
已经具有增序,按照上述算法描述,对于长度为n的数组一次划分,如果出现指针交叉,所执行的比较是 n+1 次(工作指针的边界元素的比较),即Θ(n)。
- 效率分析
最坏情况(已具有增序):在进行了n+1次比较后建立了分区,还会对数组进行排序, 继续到最后一个子数组A[n-2…n-1]。总比较次数为:

最好情况:每次都是等分

平均复杂度:分裂点有可能在一次分区后出现在每个位置
设每种情况出现的概率均等,即均为是1/n,则平均复杂度满足如下递归方程:
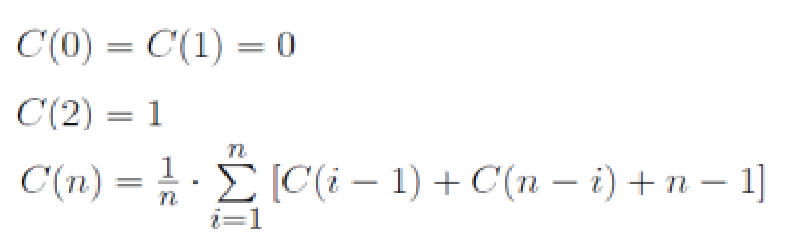
总结
