前言

Github：Leetcode-11. Container With Most Water(代码实现)

题目

Leetcode-11. Container With Most Water

Leetcode-cn-11. 盛最多水的容器

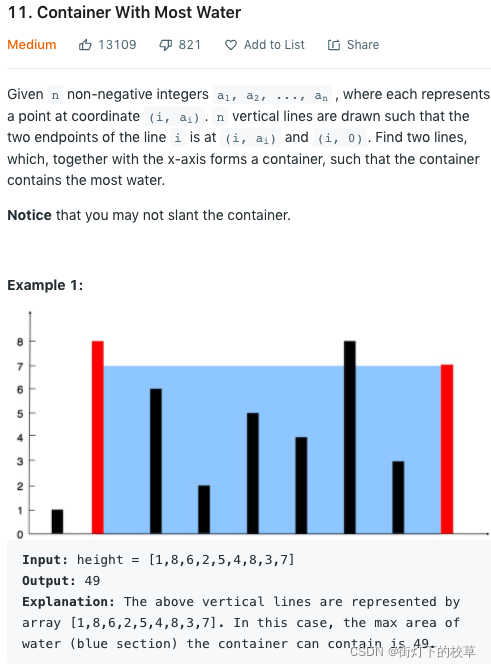
题目含义

在 x 轴上寻找坐标与原点之间线段 a，在 y 轴上寻找线段 b，求 a 与 b 构成矩形的最大面积值，

即求 a * b 的最大值。

算法思路

双指针解题技巧。左右两个指针，每次移动构成矩形，计算所构成矩形的面积是否是最大值，

最后返回最大矩形的面积值。

算法代码

package com.jpeony.leetcode.n0011;

/**
 * [11. Container With Most Water](https://leetcode.com/problems/container-with-most-water/)
 * [11. 盛最多水的容器](https://leetcode-cn.com/problems/container-with-most-water/)
 *
 * @author yihonglei
 */
public class N11_ContainerWithMostWater {

    /**
     * 【双指针】
     * 时间复杂度：O(n)。整段代码占用时间最多的是 for 循环，循环了 n 次，n 为数组的长度，
     * 所以时间复杂度是 O(n)。
     * 空间复杂度：O(1)。整个算法计算过程中，只用了一个存储临时最大值的变量空间，
     * 所以空间复杂度是 O(1)。
     */
    private static int maxArea(int[] height) {
        // 左右指针
        int left = 0, right = height.length - 1;
        // 最大面积
        int maxArea = 0;
        while (left < right) {
            // 宽：右指针位置与左指针位置横坐标之差距离
            int width = right - left;
            // 高：右指针位置与左指针位置纵坐标最小值，只有取最小值才能与另外一边连线构成矩形
            int high = 0;
            if (height[left] <= height[right]) {
                high = height[left];
                left++;
            } else {
                high = height[right];
                right--;
            }
            // 当前矩阵面积
            int curArea = width * high;
            // 所有构成矩阵的最大面积
            maxArea = Math.max(curArea, maxArea);
        }

        return maxArea;
    }

    public static void main(String[] args) {
        int[] height = {1, 8, 6, 2, 5, 4, 8, 3, 7};
        System.out.println("maxArea = " + maxArea(height));
    }
}