给定一棵树的前序遍历?preorder?与中序遍历??inorder。请构造二叉树并返回其根节点。
示例一:
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例二:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder?和?inorder?均无重复元素
inorder?均出现在?preorder
preorder?保证为二叉树的前序遍历序列
inorder?保证为二叉树的中序遍历序列
解题思路:这道题是数据结构笔试的一道常考题,经常会出选择题,我们可以利用前序遍历和中序遍历的性质来完成原二叉树的构建,因为题目告诉了我们每个节点都是不相同的,所以保证了我们构建的二叉树的唯一性。
前序遍历的特点:第一个节点为根节点,所有的左子树节点都在右子树节点之前,如下图所示:
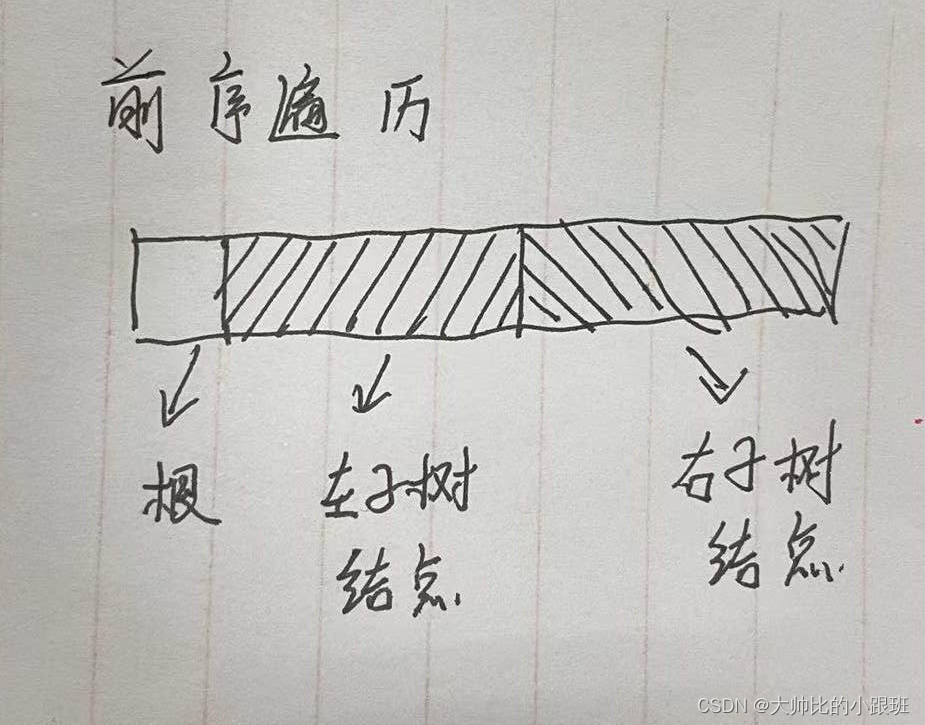
?中序遍历的特点:前半部分为左子树节点,中间为根节点,剩余部分为右子树节点,如下图所示:
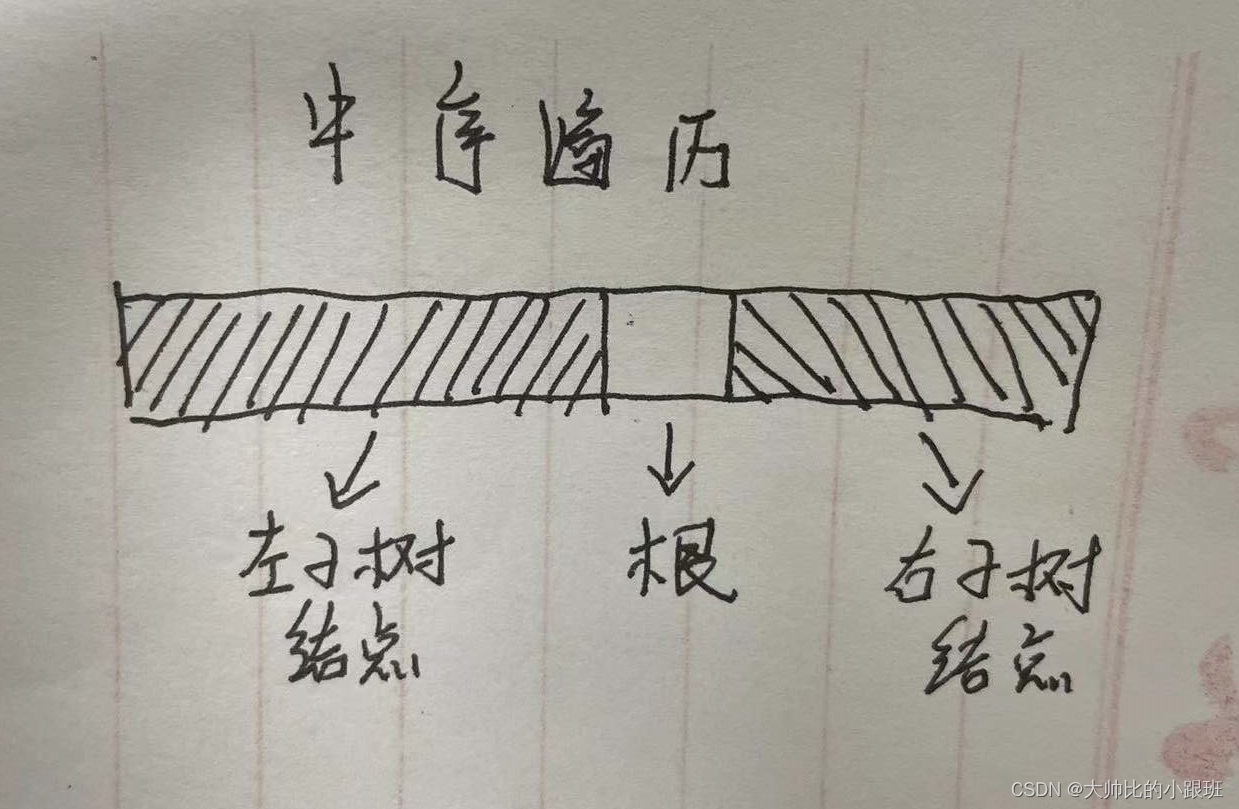
?我们可以使用一个哈希表将中序遍历的每一个节点的值及其数组下表存储起来,每次使用前序遍历的第一个节点寻找中序遍历根节点的下表,从而计算出左子树和右子树的长度。从而计算出左子树和右子树先序遍历数组和中序遍历数组进行递归,最后返回根节点即可。
实现代码和提交截图如下图所示:
class Solution {
HashMap<Integer,Integer> map = new HashMap();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for(int i = 0 ; i < inorder.length ; i++){
map.put(inorder[i],i);
}
return dfs(preorder,inorder,0,preorder.length-1,0,inorder.length-1);
}
//lp,rp代表递归的先序遍历数组左侧下标及右侧下标,这样可以在原数组上截取新的先序遍历数组。
//li,ri代表递归的中序遍历数组左侧下标和右侧下标,这样可以在原数组上截取新的中序遍历数组。
private TreeNode dfs(int[] preorder, int[] inorder , int lp , int rp , int li , int ri){
if(lp > rp){
return null;
}
TreeNode node = new TreeNode(preorder[lp]);
int index = map.get(node.val);
int lsize = index - li;
int rsize = ri - index;
//先序的左子树[lp + 1 ,lp + lsize] 右子树[lp + lsize + 1,rp]
//中序的左子树[li , index - 1] 右子树[index + 1 ,ri]
node.left = dfs(preorder,inorder,lp + 1,lp + lsize,li,index - 1);
node.right = dfs(preorder,inorder,lp + lsize + 1,rp,index + 1,ri);
return node;
}
}
?总结:二叉树的本身就是一个递归,加油。