位置式PID算法

??位置式
P
I
D
PID
PID算法是一种比较直观的的
P
I
D
PID
PID算法,如系统框图中所示,
i
n
in
in表示设定值,
e
r
r
o
r
error
error表示差值,
u
u
u表示控制器输出值,
o
u
t
out
out表示被控量。算法表达式如下:

增量式PID算法
??增量式
P
I
D
PID
PID算法不比位置式更直观,当执行机构需要控制量的增量时,适合采用增量式
P
I
D
PID
PID算法,比如步进电机控制。算法表达式如下:
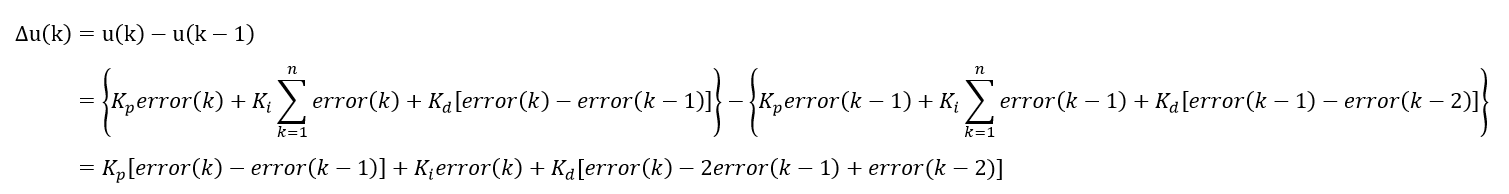

积分分离PID算法
??
P
I
D
PID
PID算法中,积分可消除稳态误差,提高控制精度,在系统启动或设定值大幅改变时,被控量与设定值之间会产生较大的偏差,造成过大的积分积累,甚至使控制量超过执行机构允许最大动作范围对应的极限控制量,引起系统过大的超调量,从而振荡,为避免这些不利的情况出现,可在被控量与设定值之间有较大偏差时,取消积分作用,避免超调量增大;当被控量接近设定值时,引入积分控制,消除稳态误差,提高控制进度。
??设被控量与设定值之间的偏差阈值为
X
>
0
X>0
X>0,该值人为设定,即

算法表达式如下:
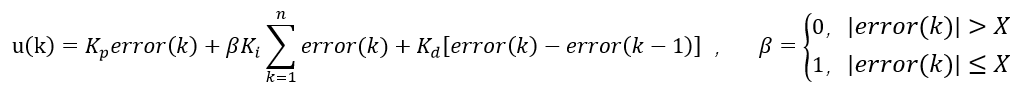
梯形积分PID算法
??在
P
I
D
PID
PID算法中,积分项的作用就是为了消除稳态误差,故而提高积分项的运算精度能更好的提高控制精度。在单片机中,对于积分运算通常使用累加的形式,也就是矩形积分,即
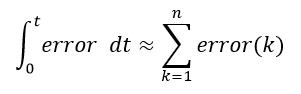
上述式子在程序中经常这样使用,但在
P
I
D
PID
PID算法中,并不是这样,这不得不从原始的
P
I
D
PID
PID算法说起,其表达式如下所示。
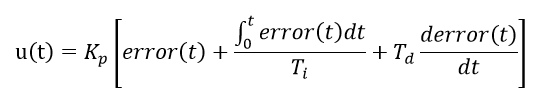
将其离散化,令
t
=
k
T
t=kT
t=kT,得
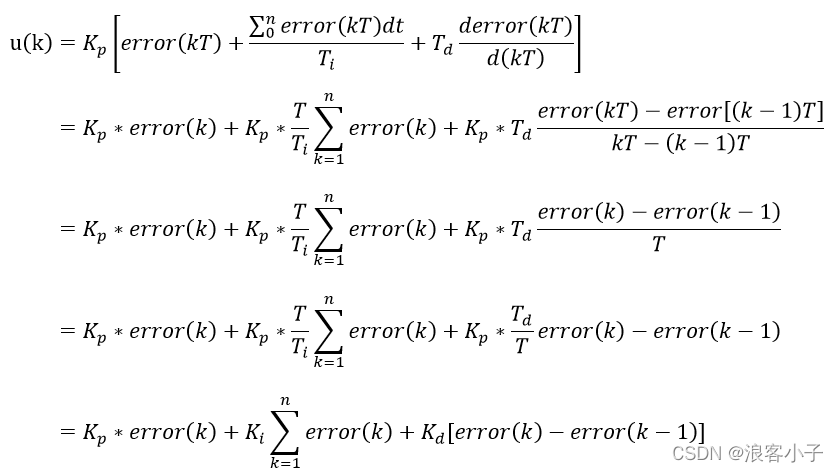
也就是说,从严格意义来讲,积分项应该为
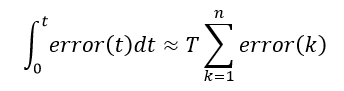
为方便编程计算把系数项全部整合在一块,称之为积分系数,所以就把
T
T
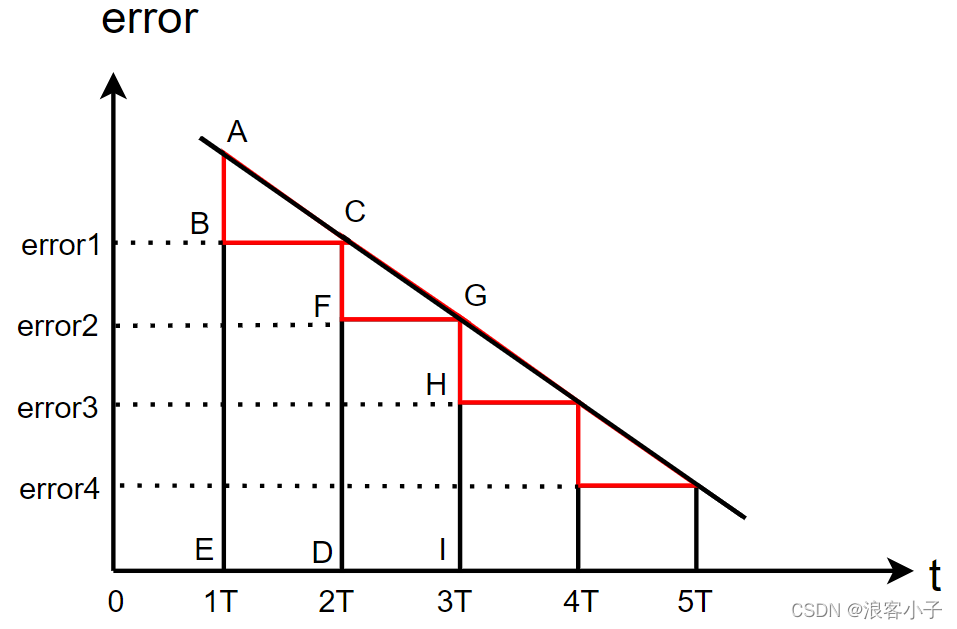
T省略了。积分从图像上来看,就是求面积。因此在单片机中计算积分的思路就是把图形划分为宽度为
T
T
T的
n
n
n个等份,然后在每个等份中自图形曲线以下画出一个最大矩形,然后将所有矩形面积相加便可近似为求积分的过程。
T
T
T越小矩形面积和越接近于积分运算,但在实际工程中,
T
T
T不可能太小,因为
T
T
T实际上就是采样时间,也是
P
I
D
PID
PID的计算周期,
T
T
T过小会加大单片机的负担。这样的计算方式很直观,但计算的精度较低,误差大。假设偏差
e
r
r
o
r
error
error在某段时间服从函数
f
(
e
r
r
o
r
)
=
?
a
?
e
r
r
o
r
+
b
f(error)=-a*error+b
f(error)=?a?error+b,如下所示
那么积分运算就是指
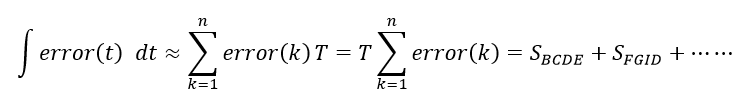
很明显,这使得每个矩形上面的三角形都未参与计算,使得积分运算精度大大降低,为避免出现过大的误差或者进一步提高运算精度,引入梯形积分的概念,就是把矩形和三角形加在一起,也就是梯形的面积,即
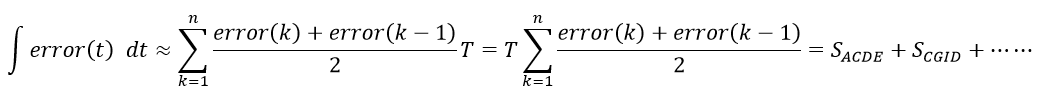
故梯形积分的
P
I
D
PID
PID的表达式为
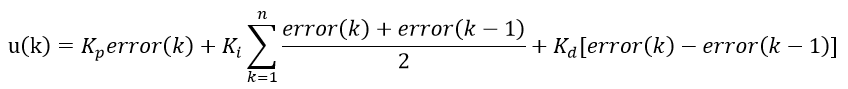
??当偏差
e
r
r
o
r
error
error不服从线性关系,或者是其他一些曲线,则不会向示例中那般毫无误差,仍会有些许误差无法计算到,但同矩形积分相比,运算精度已经得到了很大的改善。
变速积分PID算法
??变速积分
P
I
D
PID
PID算法与积分分离
P
I
D
PID
PID算法本质上相同,都是为了减小系统超调,提高系统响应速度,但是积分分离
P
I
D
PID
PID算法较为粗暴,变速积分
P
I
D
PID
PID算法则是根据偏差
e
r
r
o
r
error
error的大小来改变积分的速度,偏差越大,积分越慢,反之越快。即积分项的表达式为
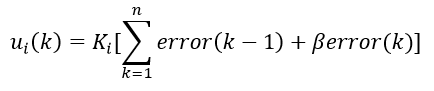
β
β
β是关于偏差
e
r
r
o
r
error
error的函数,即
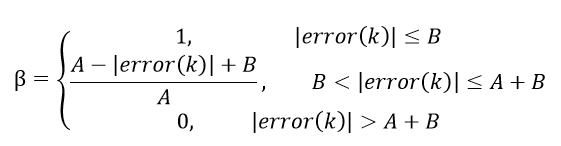
其中
A
,
B
A,B
A,B表示人为设定的阈值,则变速积分PID算法的表达式为
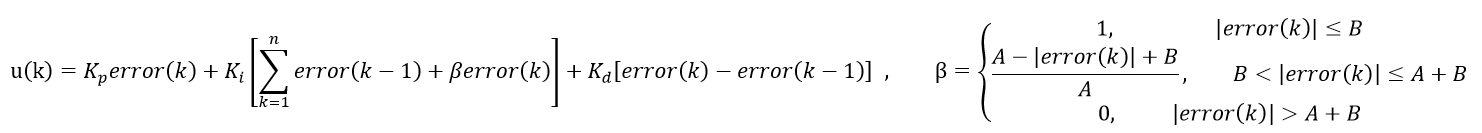
带滤波器的PID算法
??当系统中存在高频干扰时,会使得系统变得不稳定,另外,在
P
I
D
PID
PID算法中,微分项会将高频干扰放大,所以需要将高频干扰过滤掉,从而使系统稳定,故引入低通滤波器。假设该滤波器传递函数为
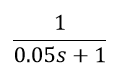
该滤波器的转折频率为20
H
z
Hz
Hz,对如下系统
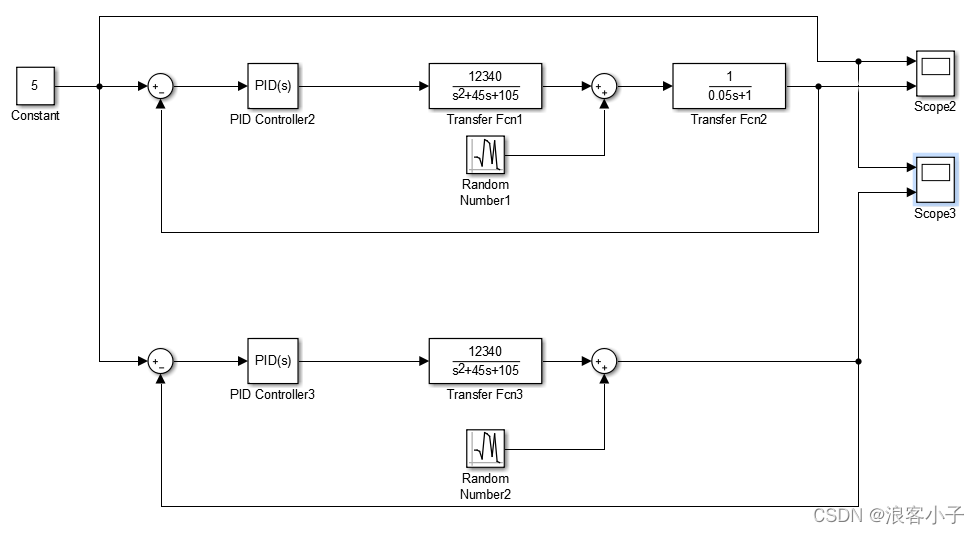
当干扰信号频率低于20
H
z
Hz
Hz,设为10
H
z
Hz
Hz,输出曲线如下

左图为带滤波器的输出响应,右图不带滤波器,可以看出此时两个系统输出很不稳定,波动都很大,再看看干扰信号频率大于20
H
z
Hz
Hz时的情况,设为100
H
z
Hz
Hz,输出曲线如下

很明显,此时带有滤波器的系统输出相比于之前10
H
z
Hz
Hz干扰信号时的输出波动幅度要小很多,此时不带滤波器的系统输出已经受到剧烈干扰,带有滤波器的系统输出波动幅度更小。在加大干扰信号的频率,设为10
k
H
z
kHz
kHz,输出曲线如下

此时带有滤波器的系统输出几乎已经没有了波动。
??在编程中使用带滤波器的
P
I
D
PID
PID算法时,需要对滤波器的传递函数进行
Z
Z
Z变换并离散化。
基于前馈补偿的PID算法
??对于设定值变化的系统中,为提高系统的跟踪性能,需要加入前馈补偿。既然是提高系统的跟踪性能,那自然就是系统的输出越接近于甚至等于系统的输入,也就是闭环系统的传递函数为
1
1
1。如下图所示


??假设有一个被控对象为
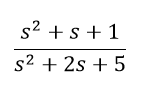
不加前馈补偿,如下

系统输入为正弦信号,输出图像如下
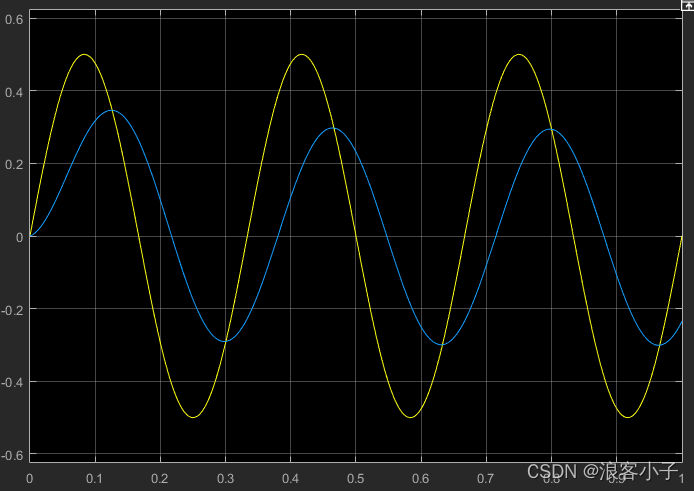
??黄线表示系统输入的信号曲线,蓝线表示系统输出曲线,可以看出,输出曲线不仅幅值较系统输入小,且滞后于系统输入,再来看看加入前馈补偿的效果,系统框图如下

输出曲线如下

此时只能看到一条曲线,因为输入曲线与输出曲线重合了,此时的跟踪效果较之前有了很大的提升。在编程中,使用前馈补偿的
P
I
D
PID
PID算法,在计算uf时,可对
1
/
G
(
s
)
1/G(s)
1/G(s)进行
Z
Z
Z变换并离散化。