文章目录
一. 概念定义
1.1 矩阵定义
??矩阵的定义是按照长方阵列排列的负数或实数集合,如下所示,表示一个4 × 3的矩阵。
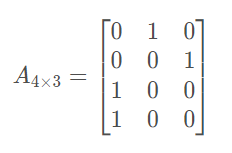
在C语言中,我们通常用二维数组来表示矩阵,例如arr[m][n] 表示一个m × n的矩阵,其中arr[ i ] [ j ] 表示矩阵的第 i 行,第 j 列的元素。
1.2 矩阵的水平翻转
??矩阵的水平翻转就是将矩阵的每一行的元素进行逆序,例如我们将上图矩阵翻转的结果为:
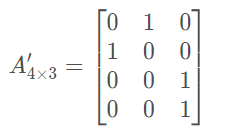
1.3 矩阵的垂直翻转
??垂直翻转就是将矩阵的每一列进行逆序,同样对1.1中的矩阵进行翻转,结果为:
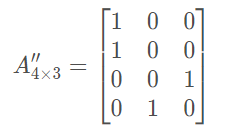
1.4 矩阵顺时针旋转
??矩阵顺时针旋转90度,这是后行列会交换,所以旋转结果为:
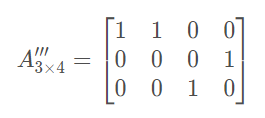
1.5 矩阵的逆时针旋转
??逆时针旋转90度其实就是顺时针旋转270度,所以我们进行三次顺时针旋转90度即可。
1.6 矩阵转置
??矩阵的转置,就是对矩阵的主对角线对称的元素进行交换的操作,转置结果如下:
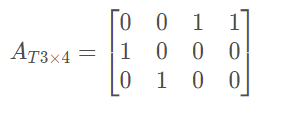
二. 推荐专栏
三. 相关练习
3.1 最富有客户的资产总量
思路分析
我们只需遍历每个account,比计算其资产,然后比较出最大的资产即可
代码如下:
int maximumWealth(int** accounts, int accountsSize, int* accountsColSize){
int max = 0;
for(int i = 0; i < accountsSize; i++){
int sum = 0;
for(int j = 0; j < *accountsColSize; j++){
sum += accounts[i][j];
}
max = fmax(max, sum);
}
return max;
}
3.2 翻转图像
思路分析
题目要求我们先进行水平翻转,然后进行反转,由于每一行的这两个操作都是相互独立,互补干扰的,所以我们可以同时进行。
代码如下:
int** flipAndInvertImage(int** image, int imageSize, int* imageColSize, int* returnSize, int** returnColumnSizes){
*returnSize = imageSize;
*returnColumnSizes = imageColSize;
for(int i = 0; i < imageSize; i++){
int l = 0;
int r = *imageColSize - 1;
//水平翻转
while(l < r){
//首位进行交换
int tmp = image[i][l];
image[i][l] = image[i][r];
image[i][r] = tmp;
l++;r--;
}
//反转
for(int j = 0; j < *imageColSize; j++){
if(image[i][j] == 0)image[i][j] = 1;
else image[i][j] = 0;
}
}
return image;
}
3.3 转置矩阵
思路分析:
转置矩阵,就是将行转化为列,我们根据matix[ i ][ j ]定义一个数组ret[ j ][ i ],然后遍历数组matix,进行赋值ret[ j ] [ i ] = matix [ i ][ j ]即可
代码如下:
int** transpose(int** matrix, int matrixSize, int* matrixColSize, int* returnSize, int** returnColumnSizes){
*returnSize = *matrixColSize;
int size = matrixSize;
int col = *matrixColSize;
*returnColumnSizes = (int*) malloc(sizeof(int) * col);
int** ret = (int**)malloc(sizeof(int*) * col);
for(int i = 0; i < col; i++){
ret[i] = (int*) malloc(sizeof(int) * size);
(*returnColumnSizes)[i] = size;
for(int j = 0; j < size; j++){
ret[i][j] = matrix[j][i];
}
}
return ret;
}