?????小饼干先喂饱小胃口
原题如下:
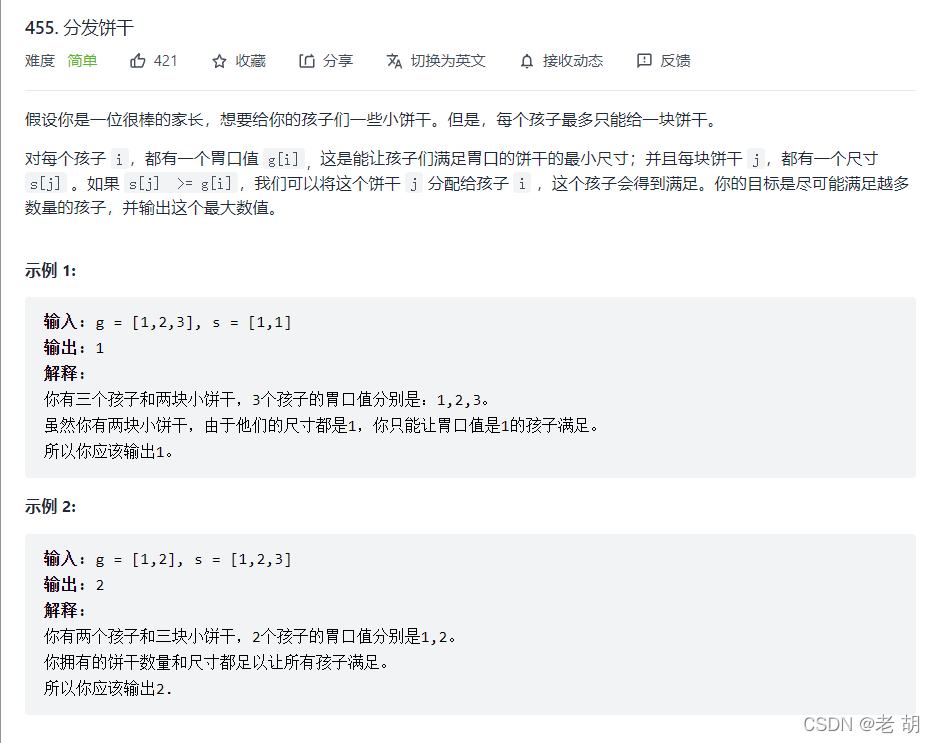
??假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
??对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
审题:
?? 光看题目可能有点晦涩难懂,在这里结合示例再来给大家解释一下。
?? g数组的大小代表的是孩子个数,g数组中的数据元素代表每个孩子对应的最低胃口值。s数组的大小代表饼干数量,s数组中的数据元素代表每块饼干对应的尺寸。
?? 如果尺寸>=最低胃口值则说明这块饼干能满足这个孩子,那么就将这块饼干给孩子吃。
?? 题目要求我们返回能满足孩子的最大数量。
思路:
??题目要求解能满足孩子的最大数量,那如何能保证满足最多的孩子?当用尺寸最小的饼干满足胃口值最低的孩子,就能保证满足最多的孩子(其实这也是贪心算法的思想)。
??要以最小满足最低,则要事先将孩子按胃口值小到大排序,将饼干按尺寸小到大排序。
??当排序完成后……现在假设有如下的两组有序数据,分别代表孩子与饼干,如下:
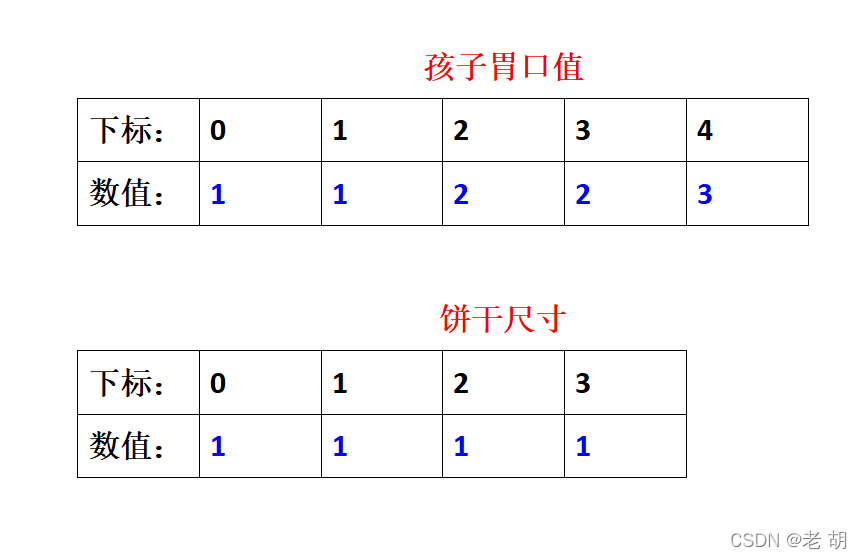
??用两指示指针,指示当前位置,如下:
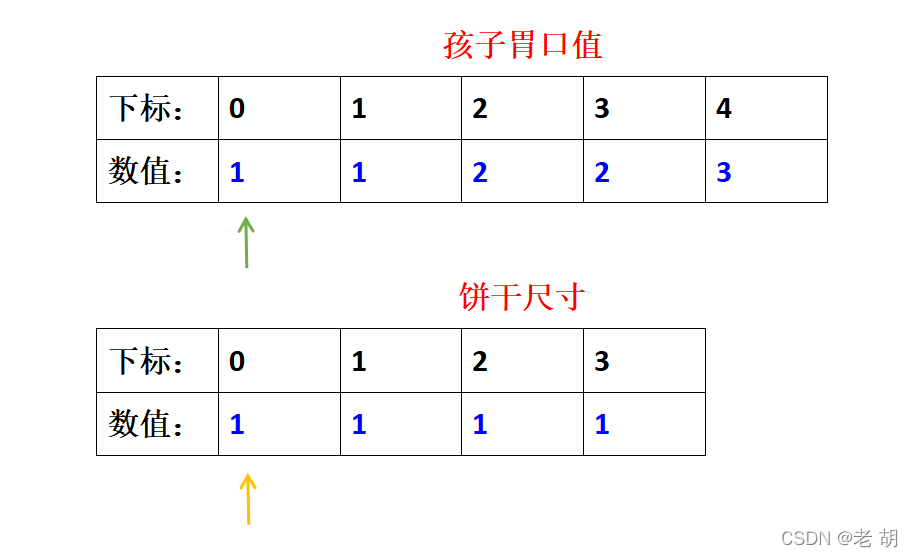
??比较当前位置,若饼干尺寸>=孩子胃口值,则让两指针都指向下一个位置……若饼干尺寸不满足孩子最低胃口值,则让指示饼干尺寸的指针指向下一个饼干……
??当满足了所有的孩子,则结束;当遍历完了所有的饼干则结束。
代码实现:
??也就是说如果这两组数据若有序,则问题将会变得很简单,应而事先对数据进行排序。
??在这里可以调用C++库中的排序方式对数据进行排序,也可以自行设计排序算法。
??我在这里采用归并排序的思想来设计排序算法,有关归并排序的知识,在我往期的文章中有介绍,有兴趣的可以了解一下。
??归并排序详解
利用C++库排序实现:
//C++实现
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
int child=0;//标记孩子
int cookie=0;//标记饼干
sort(g.begin(),g.end());//对g数组排序
sort(s.begin(),s.end());//对s数组排序
while(child<g.size()&&cookie<s.size())
{
if(s[cookie]>=g[child])//如果满足则将这块饼干给孩子
{
child++;
}
cookie++;
}
return child;//此时child的值就是最大数值
}
};
利用归并排序实现:
//C实现:
void merge(int *array,int*tempAry,int left,int mid,int right)//进行合并的入口函数
{
//其实这一部分就是大家熟悉的有序表的合并
int left_pos=left;//标记mid左半区第一个数据
int right_pos=mid+1;//标记mid右半区第一个数据
int pos=left;//标记辅助数组位置,切记初始位置一定是left
while(left_pos<=mid&&right_pos<=right)
{
if(array[left_pos]>array[right_pos])//右半区的元素更小
{
tempAry[pos++]=array[right_pos++];
}
else//左半区的元素更小
{
tempAry[pos++]=array[left_pos++];
}
}
while(left_pos<=mid)//左半区还有剩余元素
{
tempAry[pos++]=array[left_pos++];
}
while(right_pos<=right)//右半区还有剩余元素
{
tempAry[pos++]=array[right_pos++];
}
while(left<=right)//将数据拷贝回原始数组
{
array[left]=tempAry[left];
left++;
}
}
void mergeSortDi(int *array,int *tempAry,int left,int right)//进行划分的入口函数
{
if(left<right)//当只剩下一个数据时,开始返回
{
int mid=(left+right)/2;
mergeSortDi(array,tempAry,left,mid);//对左边的数据递归划分
mergeSortDi(array,tempAry,mid+1,right);//对右边的数据递归划分
merge(array,tempAry,left,mid,right);//划分结束后进行合并
}
}
void mergeSort(int*array,int size)//归并排序的入口函数
{
int *tempAry=(int*)malloc(sizeof(int)*size);//辅助数组,用于进行合并的辅助数组
if(tempAry)
{
mergeSortDi(array,tempAry,0,size-1);//先进行划分
free(tempAry);//释放辅助数组
}
}
int findContentChildren(int* g, int gSize, int* s, int sSize){
//调用归并排序的入口函数完成对数据的排序
mergeSort(g,gSize);//完成对g数组的排序
mergeSort(s,sSize);//完成对s数组的排序
int child=0;//标记孩子
int cookie=0;//标记饼干
while(child<gSize&&cookie<sSize)
{
if(s[cookie]>=g[child])//如果饼干能满足孩子就给孩子
{
child++;
}
cookie++;
}
return child;
}
序:
??我还是不太推荐大家调用库中的排序,利用这些题目可以很好的巩固我们对各种排序算法的掌握程度。就像这里当我再次设计归并排序算法时,很多细节还是没有考虑到,经常出错,当然也从侧面反映出我掌握的还是不够好。我也常常告诉自己,慢点没事儿,只要有收获就行。
??好了,这次的分享到这里。
??我是老胡,感谢阅读!!!?? ??