[数据结构与算法] 红黑树学习笔记（自己实现一个简单的红黑树）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 红黑树学习笔记（自己实现一个简单的红黑树） -> 正文阅读

[数据结构与算法]红黑树学习笔记（自己实现一个简单的红黑树）

最近在学习树的一些东西，想把树从头开始总结一下巩固自己的印象。

1、树结构入门

1.1、什么是树？

树（tree）是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点通过连接它们的边组成一个具有层次关系的集合。

把它叫做树是因为它看起来像一颗倒挂的树，也就是说它是根朝上的，而叶是朝下的。

树有很多种，像下面的一个节点有多余两个子节点的树，称为多路树，而每个节点最多只能有两个子节点的一种形式称为二叉树。

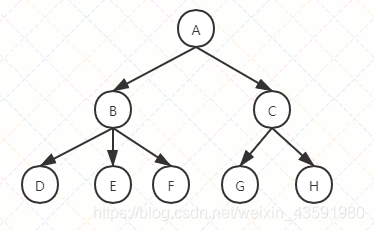
节点：上图的圈圈，比如A,B,C等都表示是节点，节点一般代表一些实体，在java面向对象编程中，节点一般代表对象。
边：连接节点的线称为边，边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。在JAVA中通常表示引用。

1.2、树结构常用术语

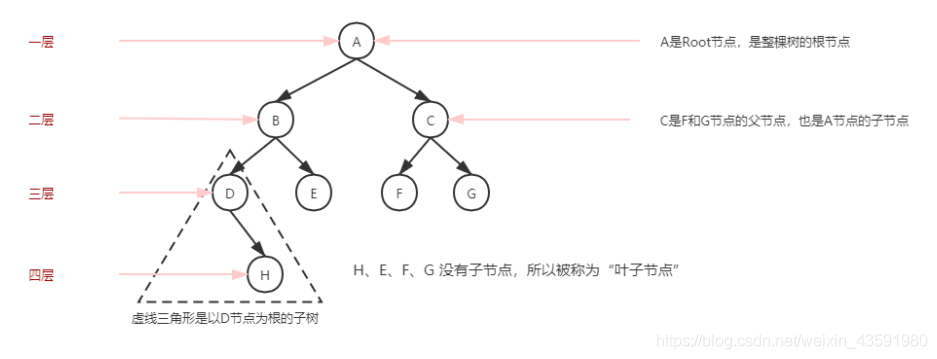
路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为路径。
根：树顶端的节点称为根。一棵树只有一个根，如果要把一个节点和边的集合称为树，那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点。
子节点：一个节点含有的子树的节点称为该节点的子节点；F、G是C节点的子节点。
兄弟节点：具有相同父节点的节点互称为兄弟节点；F、G节点互为兄弟节点。
叶子节点：没有子节点的节点称为叶子节点，也叫叶节点，比如上图的H、E、F、G都是叶子节点。
子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中。
节点的层次：从根节点开始定义，根为第一层，根的子节点为第二层，以此类推。
深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0；（从上往下看）
高度：对于任意节点n，n的高度为从n到一片树叶的最长路径长，所有树叶的高度为 0;(从下往上看)

/**
 * @author wcc
 * @date 2021/6/20 10:33
 * 分析二叉树的前序 中序 后序遍历步骤:
 * 前序遍历:
 * 1.先输出当前节点
 * 2.如果左子节点不为空 则递归继续前序遍历
 * 3.如果它的右子节点不为空 则递归继续前序遍历
 * 中序遍历:
 * 1.如果当前节点的左子节点不为空 则递归中序遍历
 * 2.输出当前节点
 * 3.如果当前节点的右子节点不为空 则递归进行中序遍历
 * 后序遍历:
 * 1.如果当前节点的左子节点不为空 则递归后序遍历
 * 2.如果当前节点的右子节点不为空 则递归后序遍历
 * 3.输出当前节点
 * <p>
 * 使用前序 中序 后序的方式来查询指定的节点
 * 前序查找思路:
 * 1.先判断当前节点的no是否等于要查找的节点的no
 * 2.如果相等 则返回当前节点
 * 3.如果不相等 则判断当前节点的左子节点是否为空 如果不为空 则递归前序遍历查找
 * 4.如果左递归前序查找 找到了节点 则返回 否则继续判断 当前节点的右子节点是否为空 如果不空
 * 则继续向右递归前序查找
 * <p>
 * 中序查找思路:
 * 1.先判断当前节点的左子节点是否为空 如果不为空 则递归中序查找
 * 2.如果找到 则返回 如果没有找到 就和当前节点比较 如果是则返回当前节点 否则继续进行右递归的中序查找
 * 3.如果右递归中序查找找到就返回 否则就返回null
 * <p>
 * 后序查找思路:
 * 1.判断当前节点的左子节点是否为空 如果不为空 则递归后序查找
 * 2.如果找到 就返回当前节点 如果没有找到 就判断当前节点的右子节点是否为空
 * 如果不为空 就进行右递归后序查找 如果找到 就返回
 * 3.就和当前节点进行比较 如果是则返回 否则返回null
 *
 * 二叉树删除节点:
 *  1>如果删除的节点是叶子节点 则删除该节点
 *  2>如果删除的节点是非叶子节点 则删除筛子树
 *
 * 思路:
 *  1>因为我们的二叉树是单向的 所以我们是判断当前的子节点是否需要删除节点
 *  而不能去判断当前这个节点是不是需要删除节点
 *  2>如果当前节点的左子节点不为空 并且左子节点就是要删除的节点 就将this.left=null即可(并且就结束递归删除)
 *  3>如果当前节点的右子节点不为空 并且右子节点就是要删除的节点 就将this.right=null
 *  4>如果第2步和第3步没有删除节点 那么我们就需要向左子树进行递归删除
 *  5>如果第2步和第3步和第4步没有删除节点 那么我们就需要向右子树进行递归删除
 *  6>还需要考虑树是空树 如果只有一个root节点 则等价于将二叉树置空
 *
 *  完全二叉树的概念:
 *      一颗深度为k的有n个节点的二叉树 对树中的节点按照从上到下 从左到右的顺序进行编号
 *      如果编号为i(1<=i<=n)的节点与满二叉树中编号为i的节点在二叉树中的位置相同 则这棵树称为完全二叉树
 *  顺序存储二叉树的概念:
 *      顺序存储二叉树的特点:
 *      1>顺序二叉树通常只考虑完全二叉树
 *      2>第n个下标的元素的左子节点的下标为2*n+1 (在数组中)
 *      3>第n个x下标的元素的右子节点的下标为2*n+2 (在数组中)
 *      4>第n个下标的元素的父节点的下标为(n-1)/2 (在数组中)
 */
public class BinaryTreeDemo {
    public static void main(String[] args) {
        //先需要创建一颗二叉树
        BinaryTree binaryTree = new BinaryTree();
        //创建需要的节点
        HeroNode heroNode1 = new HeroNode(1, "宋江");
        HeroNode heroNode2 = new HeroNode(2, "吴用");
        HeroNode heroNode3 = new HeroNode(3, "花荣");
        HeroNode heroNode4 = new HeroNode(4, "林冲");
        HeroNode heroNode5 = new HeroNode(5, "关胜");
        HeroNode heroNode6 = new HeroNode(6, "武松");
        HeroNode heroNode7 = new HeroNode(7, "鲁智深");

        //说明 我们先手动创建二叉树 后面我们学习递归的方式创建二叉树
        heroNode1.setLeft(heroNode2);
        heroNode1.setRight(heroNode3);
        heroNode2.setLeft(heroNode4);
        heroNode2.setRight(heroNode5);
        heroNode3.setLeft(heroNode6);
        heroNode3.setRight(heroNode7);

        binaryTree.setRoot(heroNode1);
        /*binaryTree.preOrder();
        System.out.println("============================");
        binaryTree.infixOrder();
        System.out.println("============================");
        binaryTree.postOrder();*/

        //System.out.println(binaryTree.postOrderSearch(3));

       // System.out.println("删除前:=============");
        binaryTree.binaryTreeBFS();
        //System.out.println("删除后:=============");
        //binaryTree.delNode(1);
        //binaryTree.preOrder();
    }
}

//定义BinaryTree类  二叉树类
class BinaryTree {
    private HeroNode root;

    public void setRoot(HeroNode root) {
        this.root = root;
    }

    //前序遍历
    public void preOrder() {
        if (this.root != null) {
            this.root.preOrder();
        } else {
            System.out.println("当前二叉树为空 无法遍历");
        }
    }

    public void preOrdeNoRecur(){
        if (this.root != null) {
            this.root.preOrdeNoRecur();
        } else {
            System.out.println("当前二叉树为空 无法遍历");
        }
    }

    public void postOrderNORecur(){
        if (this.root != null) {
            this.root.postOrderNORecur();
        } else {
            System.out.println("当前二叉树为空 无法遍历");
        }
    }

    //中序遍历
    public void infixOrder() {
        if (this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("当前二叉树为空 无法遍历");
        }
    }

    //后序遍历
    public void postOrder() {
        if (this.root != null) {
            this.root.postOrder();
        } else {
            System.out.println("当前二叉树为空 无法遍历");
        }
    }

    public void binaryTreeBFS(){
        if (this.root != null) {
            this.root.binaryTreeBFS();
        } else {
            System.out.println("当前二叉树为空 无法遍历");
        }
    }

    //前序查找
    public HeroNode preOrderSearch(int no){
        if(this.root!=null){
            return this.root.preOrderSearch(no);
        }else{
            return null;
        }
    }

    //中序查找
    public HeroNode infixOrderSearch(int no){
        if(this.root!=null){
            return this.root.infixOrderSearch(no);
        }else{
            return null;
        }
    }

    //后序查找
    public HeroNode postOrderSearch(int no){
        if(this.root!=null){
            return this.root.postOrderSearch(no);
        }else{
            return null;
        }
    }

    //删除节点
    public void delNode(int no){
        if(root!=null){
            if(root.getNo()==no){
                root=null;
            }else{
                //递归删除
                root.delNode(no);
            }
        }else{
            System.out.println("空树无法删除");
        }
    }
}

//先创建HeroNode 节点
class HeroNode {
    private int no;
    private String name;
    private HeroNode left; //默认为null
    private HeroNode right; //默认null

    //在初始化节点的时候不需要初始化左右子节点 在遍历树的时候需要用来判断是否为空来进行遍历
    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }

    public HeroNode() {
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "no=" + no +
                ", name='" + name + '\'' +
                '}';
    }

    //编写前序遍历的方法
    public void preOrder() {
        System.out.println(this); //先输出当前节点
        //递归向左子树进行先序遍历
        if (this.getLeft() != null) {
            this.getLeft().preOrder();
        }
        //递归向右子树进行遍历
        if (this.getRight() != null) {
            this.right.preOrder();
        }
    }

    //中序遍历
    public void infixOrder() {
        //递归向左子树中序遍历
        if (this.getLeft() != null) {
            this.getLeft().infixOrder();
        }
        //输出当前节点
        System.out.println(this);
        //递归向右子树中序遍历
        if (this.getRight() != null) {
            this.getRight().infixOrder();
        }
    }

    //后序遍历
    public void postOrder() {
        //递归向左子树进行遍历
        if (this.getLeft() != null) {
            this.getLeft().postOrder();
        }
        //递归向右子树进行遍历
        if (this.getRight() != null) {
            this.getRight().postOrder();
        }
        //输出当前节点
        System.out.println(this);
    }

    /**
     * 二叉树前序遍历的非递归实现
     * 实现思路：先序遍历是要先访问根节点，然后再去访问左子树以及右子树，这明显是递归定义，但这里是用栈来实现的
     * 首先需要先把根节点入栈，从栈顶取出根节点，然后访问该节点，如果该节点不为空，则访问该节点，同时把该节点的右子树先入栈，然后
     * 左子树入栈。循环结束的条件是栈中不再有节点（注意，一定是右子树先入栈，然后左子树再入栈）
     */
    public void preOrdeNoRecur(){
        HeroNode temp = this; // 注意，此时this 代表的是root节点
        Stack<HeroNode> stack = new Stack<>();
        stack.push(temp); // 根节点入栈
        while (!stack.isEmpty()){ // 当栈为空的时候结束循环
            // 1.访问根节点
            HeroNode heroNode = stack.pop();
            System.out.println(heroNode);
            // 2.如果根节点存在右子树，则将右子树入栈
            if(heroNode.getRight() != null){
                stack.push(heroNode.getRight());
            }
            // 3.如果根节点存在左子树，则将左子树入栈
            if(heroNode.getLeft() != null){
                stack.push(heroNode.getLeft());
            }
        }
    }

    /**
     * 二叉树中序遍历非递归实现
     * 实现思路：中序遍历是要先遍历左子树，然后根节点，最后遍历右子树，所以需要先把根节点和其左子树入栈，直到左子树为空，
     * 此时停止入栈。栈顶节点temp就是我们需要访问的节点，取栈顶节点temp并访问该节点
     * 然后temp该节点可能有右子树，所以访问temp节点后还要判断temp节点的右子树是否为空，如果为空则接下来
     * 取出栈顶节点将其赋值给temp进行下一轮，如果不为空则将其赋值为其右子树的值循环结束的条件是栈顶节点不为空或者栈不为空
     */
    public void infixOrderNoRecur(){
        HeroNode temp = this; // 注意，此时this 代表的是root节点
        Stack<HeroNode> stack = new Stack<>();
        while (temp != null || !stack.isEmpty()){
            // 将根节点入栈
            // 2.将所有的左子树入栈
            while (temp != null){
                stack.push(temp);
                temp = temp.getLeft();
            }
            // 3.访问栈顶元素
            temp = stack.pop();
            System.out.println(temp);
            // 4.如果栈顶元素存在右子树，则将右子树赋值给temp，也就是将右孩子入栈
            if(temp.getRight() != null){
                temp = temp.getRight();
            }else{
                // 否则，将temp置为null，表示下次要访问的是栈顶元素
                temp = null;
            }
        }
    }

    /**
     * 二叉树的后序遍历非递归实现
     * 实现思路：再进行后序遍历的时候是先要遍历左子树，然后再遍历右子树，最后才遍历根节点，所以再非递归的实现中要先把
     * 根节点入栈，然后再把左子树入栈直到左子树为空，此时停止入栈。此时栈顶就是需要访问的元素，所以直接取出访问 temp
     * 再访问结束后，还要判断被访问的节点temp是否为栈顶节点的左子树，如果是的话那么还需要访问栈顶节点的右子树，所以将栈顶节点
     * 的右子树取出赋值给temp，如果不是的话则说明栈顶节点的右子树已经访问完了，那么现在可以访问栈顶节点了，所以此时将temp赋值为null
     * 判断结束的条件为temp不为空或者栈不为空，如果两个节点都不满足的话，说明所有节点都已经访问完成
     */
    public void postOrderNORecur(){
        HeroNode temp = this; // 注意，此时this 代表的是root节点
        Stack<HeroNode> stack = new Stack<>();
        HeroNode prev = null; // 代表上一次访问的节点
        while (temp != null || !stack.isEmpty()){
            // 1.将根节点及其左子树入栈
            while (temp != null){
                stack.push(temp);
                temp = temp.getLeft();
            }
            if(!stack.isEmpty()){
                // 2.获取栈顶元素
                temp = stack.peek();
                // 3.没有右子树或者已经被访问过了
                if(temp.getRight() == null || temp.getRight() == prev){
                    // 则可以访问栈顶元素
                    temp = stack.pop();
                    System.out.println(temp);
                    // 标记上一次访问的节点
                    prev = temp;
                    temp = null;
                }else {
                    temp = temp.getRight();
                }
            }
        }
    }

    // 层序遍历
    public void binaryTreeBFS(){
        List<HeroNode> temp;
        List<HeroNode> queue = new LinkedList<>();
        queue.add(this);

        while (!queue.isEmpty()){
            temp = new LinkedList<>();
            for (HeroNode node : queue){
                if(node.left != null) temp.add(node.left);
                if(node.right != null) temp.add(node.right);
                System.out.print(node.no + " ");
            }
            queue = temp;
        }
    }

    //前序遍历查找
    /**
     * @param no 编号查找的no
     * @return 如果找到就返回node 如果没有找到返回null
     */
    public HeroNode preOrderSearch(int no) {
        //先与当前节点进行比较
        if (this.getNo() == no) {
            return this;
        }
        //如果当前节点不是 则判断当前节点的左子节点是否为空 如果不为空 则递归前序查找
        //如果左递归的前序查找 找到节点 则返回
        HeroNode result = null;
        if (this.getLeft() != null) {
            result = this.getLeft().preOrderSearch(no);
        }
        if (result != null) { //说明我们左子树找到该对应节点
            return result;
        }
        //如果左递归的前序查找 找到节点 则返回 否则继续判断
        //当前节点的右子节点是否为空 如果不为空 则继续向右递归前序查找
        if (this.getRight() != null) {
            result = this.getRight().preOrderSearch(no);
        }
        return result;
    }

    //中序遍历查找
    public HeroNode infixOrderSearch(int no){
        //先判断当前节点的左子节点是否为空
        HeroNode result=null;
        if(this.getLeft()!=null){ //注意 这里必须要使用一个变量来进行接收 否则返回左子树的的最后一个子节点
            result=this.getLeft().infixOrderSearch(no);
        }
        if(result!=null){
            return result;
        }
        //如果找到 则返回 如果没有找到 就和当前节点比较 如果是则返回当前节点
        if(this.getNo()==no){
            return this;
        }
        //如果比较为falae 则继续向右递归进行中序查找
        if(this.getRight()!=null){
            result=this.getRight().infixOrderSearch(no);
        }
        return result;
    }

    //后序查找
    public HeroNode postOrderSearch(int no){
        //先判断当前节点的左子节点是否为空 如果为空 则递归向后查找
        HeroNode result=null;
        if(this.getLeft()!=null){
            result =this.getLeft().postOrderSearch(no);
        }
        if(result!=null){ //说明在左子树找到
            return result;
        }
        //如果左子树没有找到 则向右子树递归进行后序查找
        if(this.getRight()!=null){
            result=this.getRight().postOrderSearch(no);
        }
        if(result!=null){
            return result;
        }
        //如果左右子树都没有找到 就比较当前节点
        if(this.getNo()==no){
            return this;
        }
        return result;
    }

    // 递归删除节点
    // 1.如果删除的是叶子节点，则删除该节点
    // 2.如果删除的结点是非叶子节点，则删除该子树
    public void delNode01(int no){
        /**
         * 思路：
         * 1.因为我们的二叉树是单向的，所以我们是判断当前的子节点是否是删除节点
         * 而不能去判断当前这个节点是不是需要删除节点
         * 2.如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，就将this.left=null即可（并且就结束递归删除）
         * 3.如果当前节点的右子节点不为空，并且右子节点就是要删除的节点，就将this.right=null
         * 4.如果第二步和第三步没有删除节点，那么我们就需要向左子树递归删除
         * 5.如果第二步和第三步和第四步没有删除节点，我们就需要向右子树进行递归删除
         * 6.还需要考虑树是空树，如果只有一个root节点，则等价于将二叉树置空
         */
    }

    //递归删除节点
    //1.如果删除的是叶子节点 则删除该节点
    //2.如果删除的节点是非叶子节点 则删除该子树
    public void delNode(int no){
         /**
          * 思路:
          * 1>因为我们的二叉树是单向的 所以我们是判断当前的子节点是否需要删除节点
          *  而不能去判断当前这个节点是不是需要删除节点
          *  2>如果当前节点的左子节点不为空 并且左子节点就是要删除的节点 就将this.left=null即可(并且就结束递归删除)
          *  3>如果当前节点的右子节点不为空 并且右子节点就是要删除的节点 就将this.right=null
          *  4>如果第2步和第3步没有删除节点 那么我们就需要向左子树进行递归删除
          *  5>如果第2步和第3步和第4步没有删除节点 那么我们就需要向右子树进行递归删除
          *  6>还需要考虑树是空树 如果只有一个root节点 则等价于将二叉树置空
          */

        //如果当前节点的左子节点不为空 并且左子节点就是要删除的节点 就将this.left=null即可(并且就结束递归删除)
        if(this.getLeft()!=null && this.getLeft().getNo()==no){
             this.setLeft(null);
             return;
         }
        //3>如果当前节点的右子节点不为空 并且右子节点就是要删除的节点 就将this.right=null
        if(this.getRight()!=null && this.getRight().getNo()==no){
            //删除的话return回到上一个节点 然后这个节点已经被置空了 回到上一个节点继续判断右子树进行递归判断删除
            this.setRight(null);
            return;
        }
        //4>如果第2步和第3步没有删除节点 那么我们就需要向左子树进行递归删除
        if(this.getLeft()!=null){
            this.getLeft().delNode(no);
        }
        //5>如果第2步和第3步和第4步没有删除节点 那么我们就需要向右子树进行递归删除
        if(this.getRight()!=null){
            this.getRight().delNode(no);
        }
    }

    /**
     * 树的遍历方式总体分为两种：深度优先搜索（DFS）、广度优先搜索（BFS）
     * 常见的DFS：先序遍历、中序遍历、后序遍历
     * 常见的BFS：层序遍历（即按层遍历）
     *
     * 求树的深度需要遍历树的所有节点，所以有两种解法（基于深度优先遍历和广度优先遍历）
     *
     * 方法一：后续遍历（DFS）
     * 树的后序遍历 / 深度优先搜索往往利用递归或者栈来实现
     * 关键点：此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度等于左子树的深度与右子树的深度中的最大值+1
     *
     * 算法解析：
     * 递归法：
     *  终止条件：
     *   当root为空，说明已经越过叶子节点，因此返回深度0
     *  递推工作：
     *   本质上是对树做后序遍历
     *   1.计算节点 root 的左子树的深度，即调用 maxDepthh(root.left)
     *   2.计算节点 root 的右子树的深度，即调用maxDepth(root.right)
     *  返回值：
     *   返回此树的深度，即 max(maxDepth(root.left),maxDepth(root.right))+1
     *
     * 时间复杂度：O(N)，N为树的节点数量，计算树的深度需要遍历所有节点
     * 空间复杂度：O(N)，最差情况下（当树退化为链表的时候），递归的深度可达到N
     */
    public int maxDepth(){
        if(this == null){
            return 0;
        }
        return Math.max(this.left.maxDepth(), this.right.maxDepth()) + 1;
    }

    /**
     * 方法二：层序遍历
     * 树的层序遍历 / 广度优先搜索往往利用队列实现
     * 关键点：每遍历一层，则计数器+1，直到遍历完成，则可得到树的深度
     *
     * 算法解析：
     *  1.特例处理：当 root 为空的时候，直接返回深度 0
     *  2.初始化：队列 queue（加入根节点root），计数器 res = 0
     *  3.循环遍历：当 queue 为空的时候跳出
     *   3.1：初始化一个空列表temp，用于临时存储下一层节点
     *   3.2：遍历队列：遍历 queue 中的各个节点 node，并将其左子节点和其右子节点加入 temp
     *   3.3：更新队列：执行 queue = temp，将下一层节点赋值给queue
     *   3.4：统计层数：执行 res+=1，代表层数 + 1
     */
    public int maxDepth1(HeroNode root){

        if(root == null){
            return 0;
        }
        List<HeroNode> queue = new LinkedList<>();
        queue.add(root);
        List<HeroNode> temp;
        int res = 0; // 用于统计二叉树的层数

        while (!queue.isEmpty()){
            temp = new LinkedList<>();
            for (HeroNode node : queue){
                if(node.left != null){
                    temp.add(node.left);
                }
                if(node.right != null){
                    temp.add(node.right);
                }
                queue = temp;
                res ++;
            }
        }
        return res;
    }
}

1.3、二叉搜索树

如果我们给二叉树添加一个额外的条件，就可以得到一种被称作二叉搜索树（binary search tree）的特殊二叉树。

二叉树搜索树要求：若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值。

若它的右子树不空，则右子树上所有节点的值均小于它的根节点的值

它的左右子树也分别都为二叉搜索树。

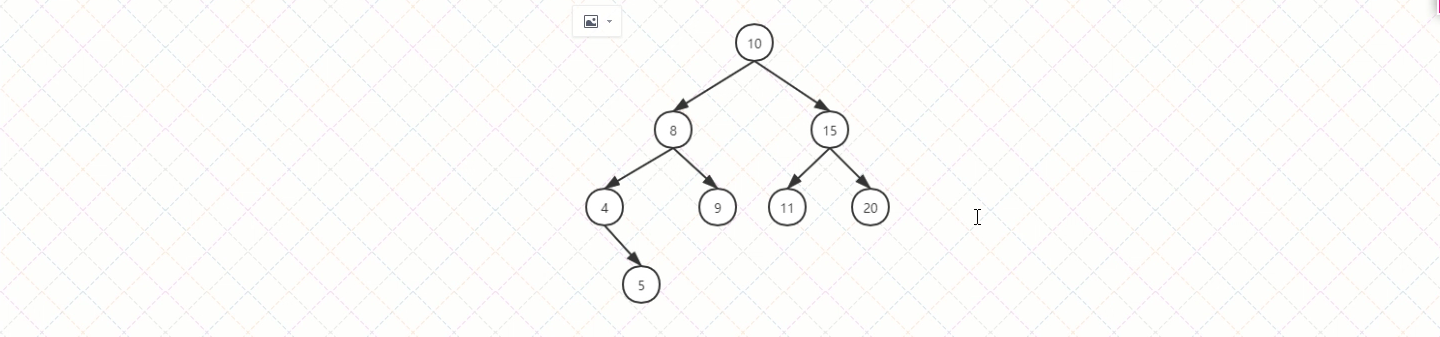
二叉搜索树 - 查找节点

查找某个节点，我们必须从根节点开始查找。

查找值比当前节点值大的话，则搜索右子树
查找值等于当前节点的值，则停止搜索（终止条件）
查找值小于当前节点值，则所搜左子树

二叉搜索树 - 插入节点

要插入节点，必须先找到插入的位置，与查找操作相似，由于二叉搜索树的特殊性

待插入的节点也需要从根节点开始进行比较，小于根节点则与根节点左子树比较，

反之则与右子树比较，直到左子树为空或者右子树为空，则插入到相应为空的位置

二叉搜索树 - 遍历节点

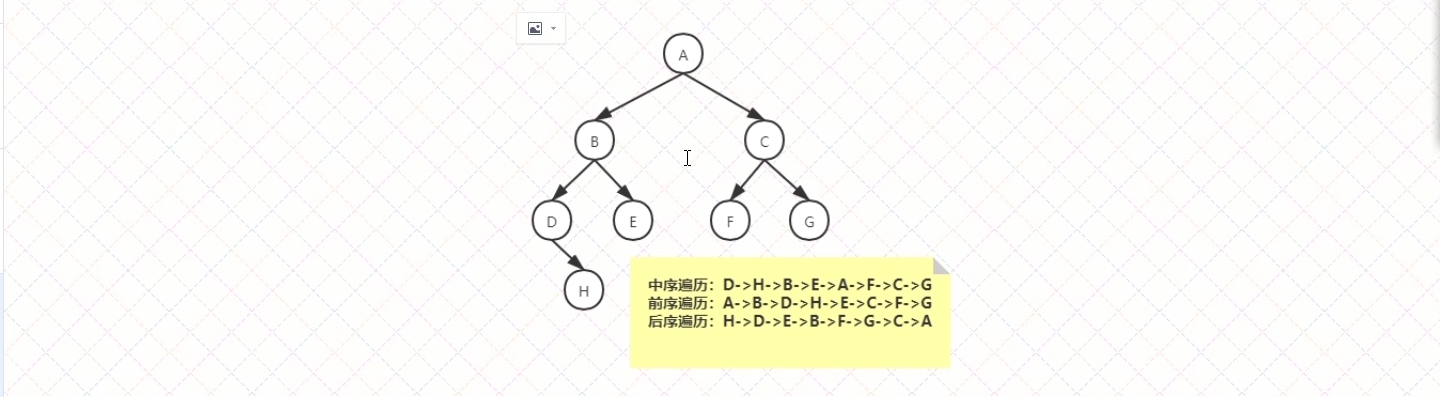
遍历树是根据一种特定的顺序访问数的每一个节点。比较常用的有前序遍历，中序遍历和后续遍历。而二叉搜索树最常用的就是中序遍历

中序遍历：左子树 —> 根节点 —> 右子树
前序遍历：根节点 —> 左子树 —> 右子树
后续遍历：左子树 —> 右子树 —> 根节点

二叉搜索树 - 查找最大值和最小值

要找最小值，先找根节点的左子节点，然后一直找这个左子节点的左子节点，直到找到没有左子节点的节点，那么这个节点就是最小值。

同理，要找最大值，一直查找根节点的右子节点，直到没有右子节点，则就是最大值。

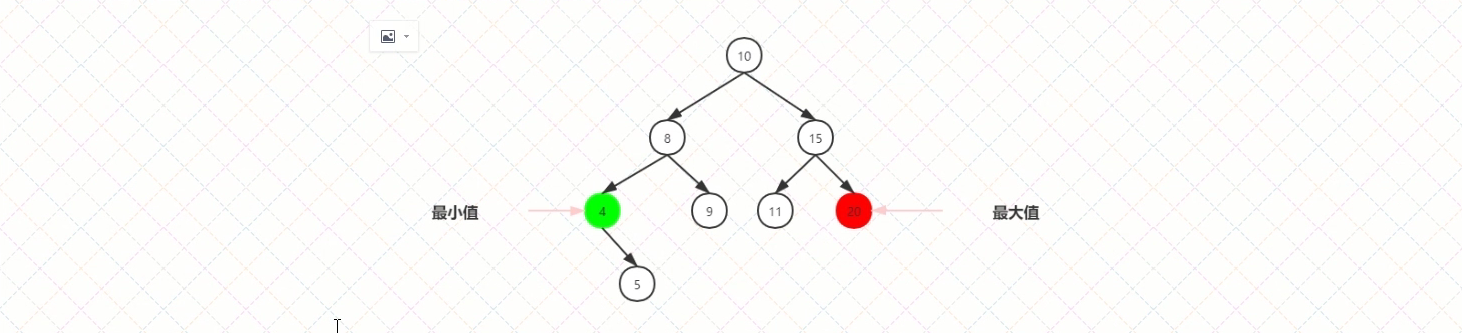
二叉搜索树 - 删除节点

删除节点是二叉搜索树中最复杂的操作，删除的节点有三种情况，前两种比较简单，但是第三种却很复杂。

该节点是叶子节点（没有子节点）
该节点有一个子节点
该节点有两个子节点

删除没有子节点的节点

要删除叶子节点，只需要改变该节点父引用该节点的值，即将引用改为 null 即可。

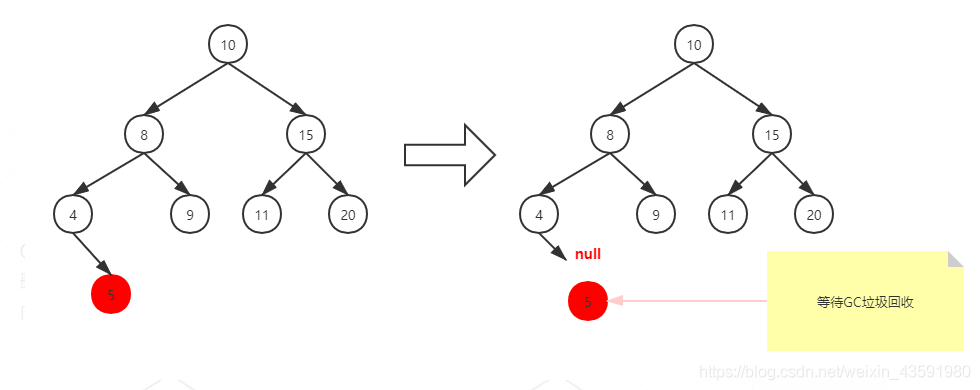
删除有一个子节点的节点

删除有一个子节点的节点，我们只需要将其父节点原本指向该节点的引用，改为指向该节点的子节点即可。

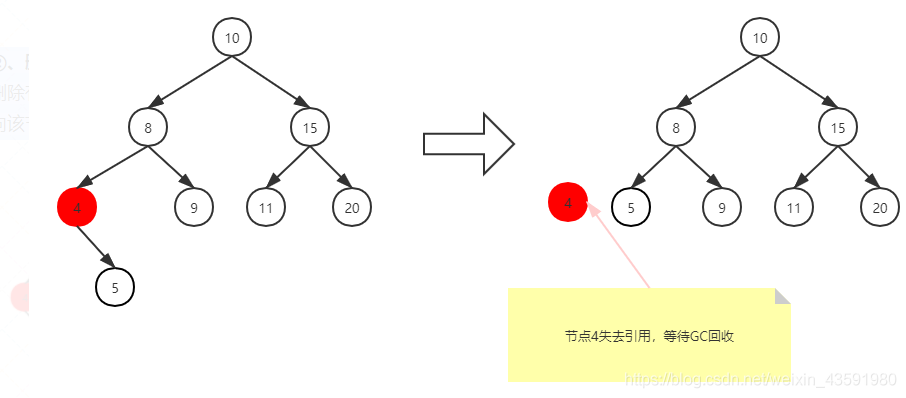
删除有两个子节点的节点

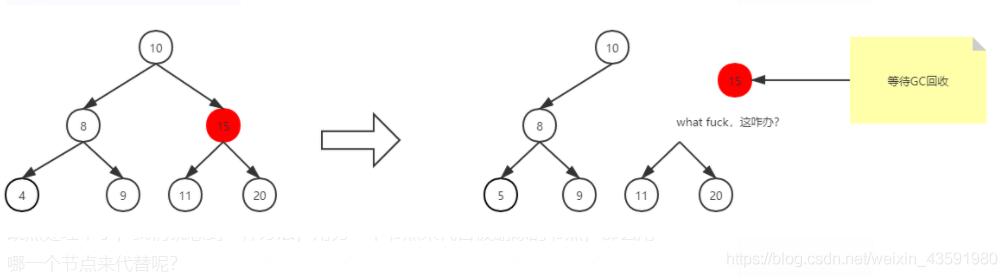
当删除的节点存在两个子节点，那么删除之后，两个子节点的位置我们就没办法处理了。

既然处理不了，我们就想到一种办法，用另一个节点来代替被删除的节点，那么用哪一个节点来代替呢 ?

我们知道二叉搜索树中的节点是按照关键字来进行排列的，某个节点的关键字的次高节点是它的中序遍历的后继节点。

用后继节点来代替删除的节点，显然该二叉搜索树还是有序的。

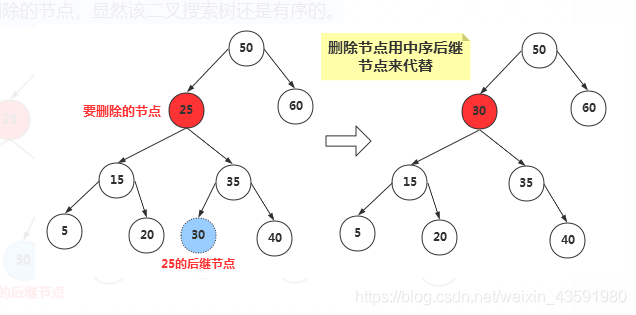
那么如何找到删除节点的中序遍历的后继节点呢？

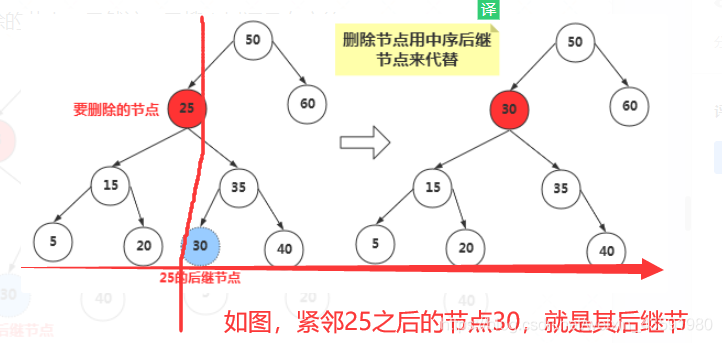
其实我们稍微分析，这实际上就是要找比删除节点关键值大的节点集合中，最小的那一个节点，只有这样代替删除节点后才能满足二叉搜索树的特性。

后继节点：比删除节点大的最小节点。

删除有必要吗？

通过上面的删除分类讨论，我们发现删除其实是挺复杂的，那么其实我们可以不用真正的删除该节点，只需要在 Node 类中添加一个标识字段 isDelete，当该字段为true的时候，表示该节点已经被删除，反之则没有删除，这样删除节点就不会改变树的结构了。

影响就是查询时需要判断一下节点是否已经被删除。

二叉树搜索树 - 时间复杂度分析

1、回顾经典 - 二分查找算法

[1，2，3，4，5，6，7，8，9。。。。100]

暴力算法：运气好的时候，性能不错，运气不好的时候，性能暴跌…

二分查找算法：数据源必须是有序数组，性能非常不错，每次迭代查询可以排除掉一半的结果

/**
 * 二分查找算法：非递归方式
 * @param arr 有序数组
 * @param data 查找的数据
 * @return index 下标，未查找到的时候返回-1
 */
public static int binarySearch(int[] arr, int data){
    int low = 0;
    int height = arr.length - 1;
    while (low <= height){
        int mid = low + (height - low) / 2;
        if(arr[mid] < data){
            low = mid + 1;
        }else if(arr[mid] == data){
            return mid;
        }else{
            height = mid - 1;
        }
    }
    return -1;
}

/**
 * 二分查找算法：递归方式
 * @param arr 有序数组
 * @param data 查找的数据
 * @param left 数组的开始下标
 * @param right 数组的尾部下标
 * @return index 下标，未查找到的时候返回-1
 */
public static int binarySearch(int[] arr, int left, int right, int data){
    // 递归结束条件
    if(left > right){
        return -1;
    }
    int mid = left + (right - left) / 2;
    if(arr[mid] < data){
        return binarySearch(arr, mid + 1, right, data);
    }else if(arr[mid] == data){
        return mid;
    }else{
        return binarySearch(arr, left, mid - 1, data);
    }
}

2、二分查找最大的缺陷是什么？

强制依赖有序数组，性能才能不错。

3、数组有什么缺陷？

没有办法快速插入，也没有办法扩容（想要扩容只能创建一个容量更大的新数组来拷贝原数组）以达到扩容的目的

4、那怎么才能拥有二分查找的高性能又能拥有链表一样的灵活性？

使用二叉搜索树

5、二分查找算法时间复杂度推算过程？

第几次查询	剩余待查询元素数量
1	N / 2
2	N / (2 ^ 2)
3	N / (2 ^ 3)
K	N / (2 ^ K)

从上表可以看出N / (2 ^ k)肯定是大于等于1，也就是N / (2 ^ K) >= 1，我们计算时间复杂度是按照最坏的情况进行计算，也就是查到剩余最后一个数才查到我们想要的数据，也就是

? N / (2 ^ K) = 1 => 2 ^ K = N => K = log2(N) => 二分查找算法时间复杂度：O(log2N) => O(logN)

普通二叉搜索树的致命缺陷：

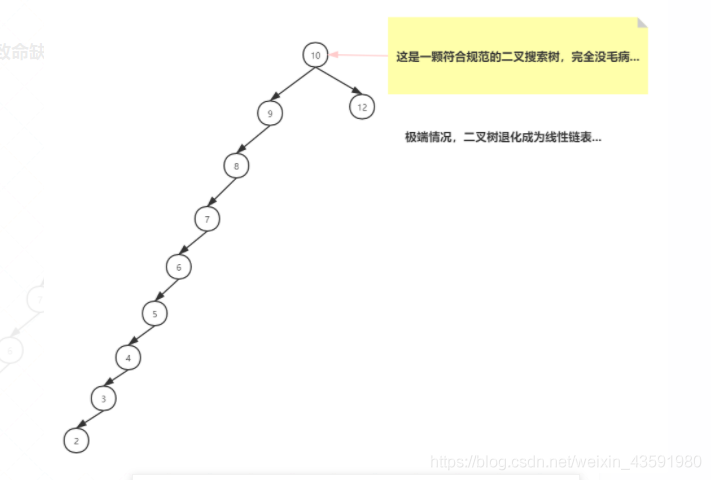
这颗二叉树的查询效率如何？

O(N)

怎么解决二叉搜索树退化成线性链表的问题？

如果插入元素的时候，树可以自动调整两边平衡，会保持不错的查找性能。

那这个时候 AVL树就应运而生，这里不再细说，推荐一个博主：java程序员 - 天天，看完以后你就明白了

这里附上 AVL 树的代码

public class BinaryTree<K extends Comparable<K>,V> {

    public static void main(String[] args) {
        BinaryTree<Integer, Object> binaryTree = new BinaryTree<>();
        /*binaryTree.insert(8,8);
        binaryTree.insert(5,5);
        binaryTree.insert(14,14);
        binaryTree.insert(7,7);
        binaryTree.insert(3,3);
        binaryTree.insert(12,12);
        binaryTree.insert(9,9);
        binaryTree.insert(4,4);
        binaryTree.insert(2,2);
        binaryTree.insert(17,17);
        binaryTree.insert(13,13);
        binaryTree.insert(15,15);
        binaryTree.insert(18,18);
        binaryTree.insert(6,6);*/
        Scanner scanner = new Scanner(System.in);
        //TreeOperation.show(binaryTree.root);
        while (true){
            System.out.println("请输入要插入的节点：");
            String next = scanner.next();
            //binaryTree.delete(Integer.parseInt(next));
            binaryTree.insert(Integer.parseInt(next),next);
            TreeOperation.show(binaryTree.root);
        }


        //TreeOperation.show(binaryTree.root);

        /*binaryTree.preOrder(binaryTree.root);
        System.out.println();
        binaryTree.infixOrder(binaryTree.root);
        System.out.println();
        binaryTree.postOrder(binaryTree.root);
        System.out.println();
        binaryTree.cengXuOrder(binaryTree.root);*/

    }

    private Node root; // 二叉树的根节点

    public Node getRoot() {
        return root;
    }

    public void setRoot(Node root) {
        this.root = root;
    }

    // 二叉查找树的插入
    public void insert(K key,V value){
        // 先判断该二叉树是否是空树
        if(this.root == null){
            this.root = new Node(key,value);
            return;
        }

        // 保存每次比较的节点，因为第一次比较的是根节点，所以此时用根节点作为起始值
        Node temp = this.root;
        // 定义其父节点
        Node parent = null;
        int i =0;
        while (temp != null){
            parent = temp;
            i = key.compareTo((K) temp.getKey());
            if( i > 0){
                temp = temp.getRight();
            }else if(i == 0){
                temp.setValue(value);
                return;
            }else{
                temp = temp.getLeft();
            }
        }
        // 注意，此时退出循环的时候，因为temp为null，而且二叉树是单向指针，所以应该以父节点来寻找要插入节点的位置
        if(i > 0){
            parent.setRight(new Node(key,value,null,null,parent));
        }else{
            parent.setLeft(new Node(key,value,null,null,parent));
        }
        // 插入的时候调整二叉树的平衡（因为我们插入的是叶子节点，所以不存在叶子节点的情况，需要从父节点开始找起）
        rebalance(parent);
    }

    // 调整二叉树的平衡（平衡二叉树的每个节点的左子树和右子树的高度最多差1）
    public void rebalance(Node node){
        // 如果父节点为空，则不需要进行平衡了
        if(node == null){
            return;
        }
        // 由于子树的平衡旋转可能影响父节点的平衡，所以要往上依次进行递推操作
        while (node != null){
            if(BFValue(node) == 2){
                // 左子树的高度 - 右子树的高度 = 2 则进行右旋操作
                /**
                 * 这里分为两种情况：该节点的左节点是否有右子节点
                 */
                Node left =node.getLeft();
                if(left.getRight() != null){
                    // 先以左子节点进行左旋操作
                    leftRoate(left);
                }
                // 左子节点没有右子节点的话以node进行右旋操作
                rightRoate(node);
            }else if(BFValue(node) == -2){
                // 这里同上也有两种情况
                Node right = node.getRight();
                if(right.getLeft() != null){
                    rightRoate(right);
                }
                leftRoate(node);
            }
            node = node.getParent();
        }
    }

    // 左旋操作
    public void leftRoate(Node a){
        if(a == null){
            return;
        }
        Node b = a.getRight();
        Node d = b.getLeft();
        // 注意，这一步不能忘，当右子树的没有左子树的时候，要把当前节点的右子树设置为空
        a.setRight(d);
        if(d != null){
            d.setParent(a);
        }
        b.setParent(a.getParent());
        if(b.getParent() != null){
            if(b.getParent().getLeft() == a){
                b.getParent().setLeft(b);
            }else{
                b.getParent().setRight(b);
            }
        }else{
            this.root = b;
        }
        b.setLeft(a);
        a.setParent(b);
    }

    // 右旋操作
    public void rightRoate(Node a){
        if(a == null){
            return;
        }
        Node b = a.getLeft();
        Node d = b.getRight();
        a.setLeft(null);
        if(d != null){
            d.setParent(a);
        }
        b.setParent(a.getParent());
        if(b.getParent() != null){
            if(b.getParent().getLeft() == a){
                b.getParent().setLeft(b);
            }else{
                b.getParent().setRight(b);
            }
        }else{
            this.root = b;
        }
        b.setRight(a);
        a.setParent(b);
    }

    // 计算左子树和右子树的高度差，也叫做平衡因子
    public int BFValue(Node node){
        // 如果当前节点为 null，则说明其没有左右子树所以高度差为0
        if(node == null){
            return 0;
        }
        return getHeighNode(node);
    }

    // 返回高度差
    public int getHeighNode(Node node){
        if(node == null){
            return 0;
        }
        return getHeight(node.getLeft()) - getHeight(node.getRight());
    }

    // 返回对应二叉树的高度
    public int getHeight(Node node){
        if(node == null){
            return -1;
        }
        return 1 + Math.max(getHeight(node.getLeft()), getHeight(node.getRight()));
    }

    // 二叉树的查找
    public Node select(K key){
        if(this.root == null){
            return null;
        }

        Node temp = this.root;
        while (temp != null){
            int i = key.compareTo((K) temp.getKey());
            if(i == 0){
                return temp;
            }else if(i > 0){
                temp = temp.getRight();
            }else{
                temp = temp.getLeft();
            }
        }
        return null;
    }

    // 前序遍历
    public void preOrder(Node root){
        // 递归结束的条件
        if(root == null){
            return;
        }
        System.out.print(root.getKey() + "  ");
        if(root.getLeft() != null){
            preOrder(root.getLeft());
        }
        if(root.getRight() != null){
            preOrder(root.getRight());
        }
    }

    // 中序遍历
    public void infixOrder(Node root){
        if(root == null){
            return;
        }
        if(root.getLeft() != null){
            infixOrder(root.getLeft());
        }
        System.out.print(root.getKey() + "  ");
        if(root.getRight() != null){
            infixOrder(root.getRight());
        }
    }

    // 后序遍历
    public void postOrder(Node root){
        if(root == null){
            return;
        }
        if(root.getLeft() != null){
            postOrder(root.getLeft());
        }
        if(root.getRight() != null){
            postOrder(root.getRight());
        }
        System.out.print(root.getKey() + "  ");
    }

    // 层序遍历
    /**
     * 1.先把根节点放入都队列中
     * 2.从队列依次弹出元素，如果元素的左右子树不为空，再把左右子树放入到队列中
     * 3.循环，直到队列为空
     */
    public void cengXuOrder(Node root){
        // 保证二叉树非空
        if(root == null){
            return;
        }
        Deque<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()){
            // 弹出队头元素
            Node remove = queue.remove();
            System.out.print(remove.getKey() + "  ");
            if(remove.getLeft() != null){
                queue.add(remove.getLeft());
            }
            if(remove.getRight() != null){
                queue.add(remove.getRight());
            }
        }
    }

    // 二叉树的删除
    /**
     * 分析：叶子节点
     * 节点有一个左子节点
     * 节点有一个右子节点
     * 节点有两个子节点
     */
    /**
     * 前驱结点：小于该节点的最大节点
     *  对二叉树中序遍历，遍历后的顺序，当前节点的前一个节点为该节点的前驱节点
     * 后继节点：大于该节点的最小节点
     *  对二叉树中序遍历，遍历后的顺序，当前结点的后一个节点为该节点的后继节点
     */
    public void delete(K key){
        // 先判断该二叉树中是否存在该节点
        Node select = select(key);
        if(select ==null){
            System.out.println("二叉树中没有该节点");
            return;
        }
        // 要删除节点，必须找到父节点，然后将其左子树或者右子树置为空
        Node parent = select.getParent();
        // 第一种情况：删除的节点是叶子节点
        if(select.getLeft() == null && select.getRight() == null){
            // 当parent 为null的时候，则代表该节点是根节点（因为父节点为空而且没有左右子树）
            if(parent == null){
                root = null;
            }else{
                // 判断要删除的节点select是parent的左子节点还是右子节点
                if(parent.getLeft() == select){
                    parent.setLeft(null);
                }else{
                    parent.setRight(null);
                }
            }
        }else if(select.getLeft() == null || select.getRight() == null){ // 说明要删除的节点只有一个子节点
            // 定义一个临时节点用来存储要删除节点的子节点
            Node temp = select.getLeft() != null ? select.getLeft() : select.getRight();
            // 如果父节点为null 说明当前节点是根节点
            if (parent == null){
                root = temp;
                temp.setParent(null);
            }else{
                if(parent.getLeft() == select){
                    parent.setLeft(temp);
                }else{
                    parent.setRight(temp);
                }
                temp.setParent(parent);
            }
        }else{ // 这种情况说明有两个子节点
            /**
             * 当有两个子节点的时候要注意一下，因为我们是通过后继节点来进行替换的，所以我们需要设置替换位置后的该后继节点的父节点
             */
            // 要先去寻找要删除节点的前驱节点或者后继节点（这里以后继节点为例）
            Node temp = sucNode(select);
            /**
             * 这里分为两种情况，后继节点是否是要删除节点的右子树
             */
            if(select.getRight() == temp){
                // 后继节点是删除节点的右子树
                if(parent == null){ // 说明要删除的节点是根节点
                    root = temp;
                    temp.setParent(null);
                }else{
                    if(parent.getLeft() == select){
                        parent.setLeft(temp);
                    }else{
                        parent.setRight(temp);
                    }
                    temp.setParent(parent);
                }
                temp.setLeft(select.getLeft());
                select.getLeft().setParent(temp);
            }else{ // 这里说明，后继节点不是要删除节点的右子树

                // 注意，此时后继节点如果有子树的话只有右子树，没有左子树，所以需要把右子树放到后继节点的父节点的左子树上
                Node replaceNodeParent = temp.getParent();

                // 这里，又分为两种情况，后继节点是否有右子树
                /**
                 * 情况1：后继节点没有右子树
                 */
                if(temp.getRight() == null){
                    // 将后继节点的左子树设置为null
                    replaceNodeParent.setLeft(null);
                }else{
                    /**
                     * 情况2：后继节点有右子树
                     */
                    replaceNodeParent.setLeft(temp.getRight());
                    temp.getRight().setParent(replaceNodeParent);
                }
                // 设置删除节点的左右子树为后继节点的左右子树
                temp.setLeft(select.getLeft());
                temp.setRight(select.getRight());
                if(parent == null){
                    root = temp;
                    temp.setParent(null);
                }else{
                    if(parent.getLeft() == select){
                        parent.setLeft(temp);
                    }else{
                        parent.setRight(temp);
                    }
                    temp.setParent(parent);
                }
            }
        }
    }

    // 寻找当前节点的后继节点
    public Node sucNode(Node node){
        Node right = null;
        if(node != null){
            right = node.getRight();
            if(right != null){
                while (right.getLeft() != null){
                    right = right.getLeft();
                }
            }
        }
        return right;
    }
}

class Node<K extends Comparable<K>,V>{
    private K key;
    private V value;

    private Node left; // 左节点
    private Node right; // 右节点
    private Node parent; // 父节点（用以实现二叉查找树）

    public Node(){

    }

    public Node(K key, V value) {
        this.key = key;
        this.value = value;
    }

    public Node(K key, V value, Node left, Node right, Node parent) {
        this.key = key;
        this.value = value;
        this.left = left;
        this.right = right;
        this.parent = parent;
    }

    public K getKey() {
        return key;
    }

    public void setKey(K key) {
        this.key = key;
    }

    public V getValue() {
        return value;
    }

    public void setValue(V value) {
        this.value = value;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    public Node getParent() {
        return parent;
    }

    public void setParent(Node parent) {
        this.parent = parent;
    }
}

为什么有了平衡树还需要红黑树？

虽然平衡树解决了二叉查找树退化为近似链表的缺点，能够把查找时间控制在O(logn)，不过却不是最佳的，

因为平衡树要求每个节点的左子树和右子树高度至多等于1，这个要求实在是太严格了，导致每次进行插入 / 删除节点的时候，

几乎都会破坏平衡树的第二个原则，进而我们都需要通过左旋和右旋来进行调整，使之再次成为一颗符合要求的平衡树。

显然，如果在那种插入、删除很频繁的场景中，平衡树需要频繁的进行调整，这会使得平衡树的性能大打折扣，为了解决这个问题，于是就有了红黑树！！

下面再学习红黑树之前，推荐先去看两篇文章，可以更好的理解下面的内容：

什么是2-3树？

清晰理解红黑树的演变—红黑的含义

红黑树的性质

性质一：每个节点要么是黑色，要么是红色
性质二：根节点是黑色
性质三：每个叶子节点的（NIL（即为 null 节点））是黑色
性质四：每个红色节点的两个子节点一定都是黑色，不能有两个红色节点相连（不然会出现2-3-4树的情况）
性质五：任意一节点到每个叶子节点的路径包含数量相同的黑色节点，俗称：黑高
性质5.1：如果一个节点存在黑色子节点，那么该节点肯定有两个子节点

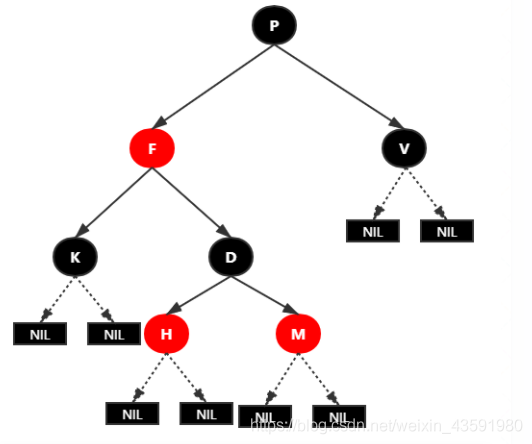
红黑树并不是一个完美平衡二叉树，可以看到，根节点 root 的左子树显然比右子树高

但左子树和右子树的黑节点的层数是相等的，也即任意一节点到每个叶子节点的路径都包括数量相同的黑节点

所以我们叫红黑树这种平衡为黑色完美平衡。

红黑树的性质讲完了，只要这棵树满足以上性质，这棵树就是趋近于平衡状态的。

不要问为什么，发明红黑树的科学家就是这么牛逼！

前面讲到红黑树能够自平衡，它靠的是什么？三种操作：左旋、右旋和变色

变色：节点的颜色由红变黑或者由黑变红
左旋：以某个节点作为支点（旋转节点），其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，（右子节点的）右子节点保持不变
右旋：以某个节点作为支点（旋转节点），其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，（左子节点的）左子节点保持不变。

左旋示意图：

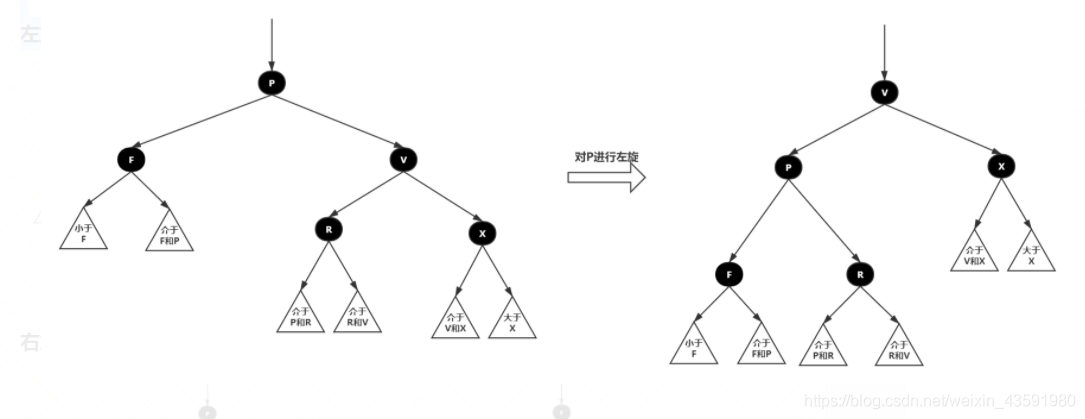
右旋示意图：

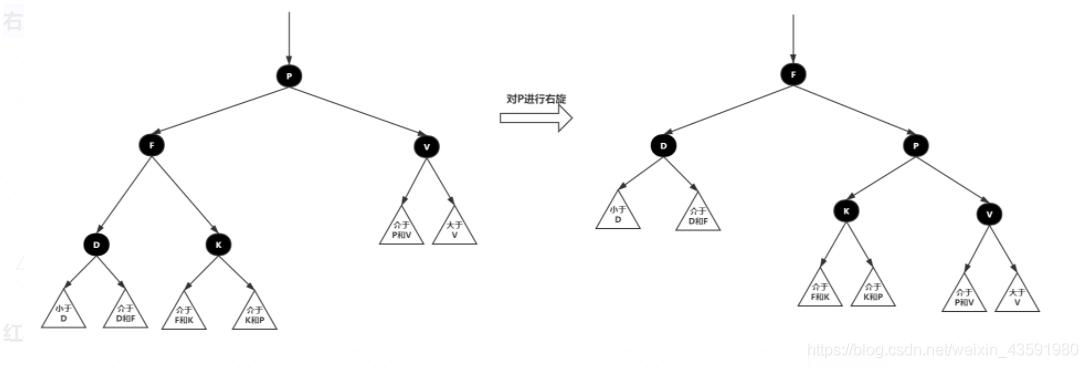
红黑树查找：

红黑树的插入：

插入操作包括两个部分工作：

1、查找插入的位置

2、插入后自平衡

注意：插入节点，必须为红色，理由很简单，红色在父节点（如果存在）为黑色节点的时候，红黑树的黑色平衡没被破坏，不需要做自平衡操作。但如果插入节点是黑色，那么插入位置所在的子树黑色节点总是多1，必须做自平衡操作。

在开始每个情景的讲解前，我们还是先来约定下：

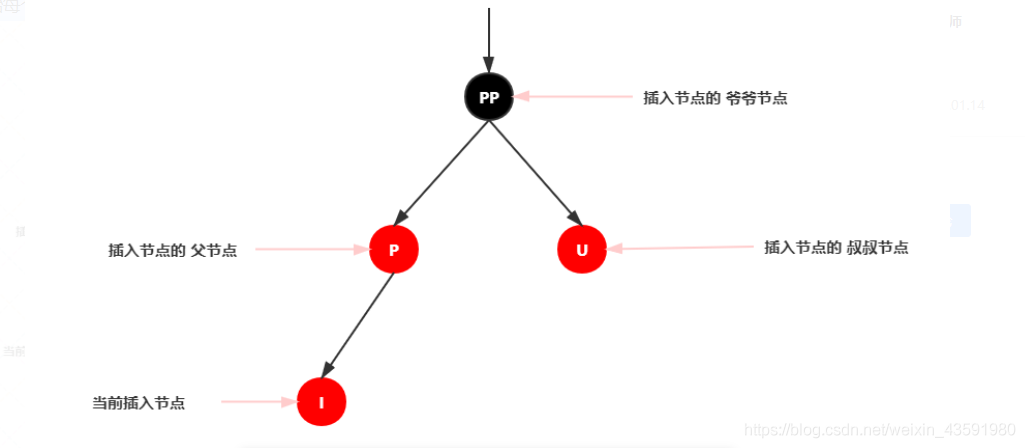
红黑树插入节点情景分析：

情景1：红黑树为空树

最简单的一种情景，直接把插入节点作为根节点就行。

注意：根据红黑树的性质2：根节点是黑色，还需要把插入节点设置为黑色

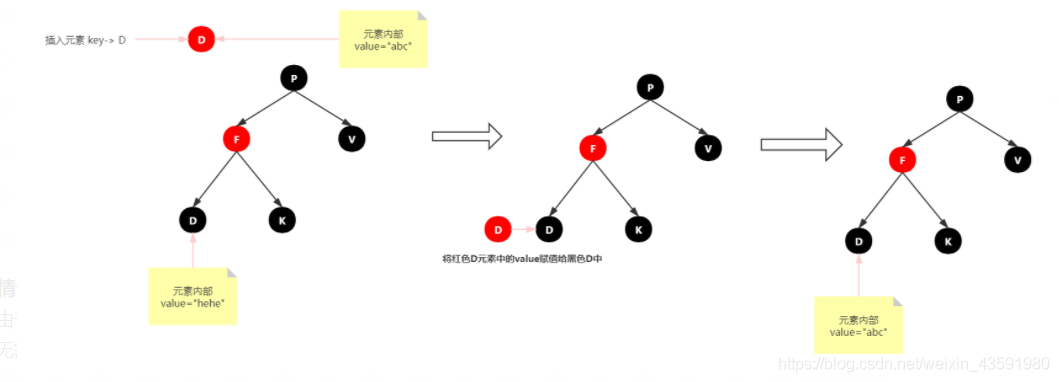
情景2：插入节点的 key 已经存在

处理：更新当前节点的值，为插入节点的值

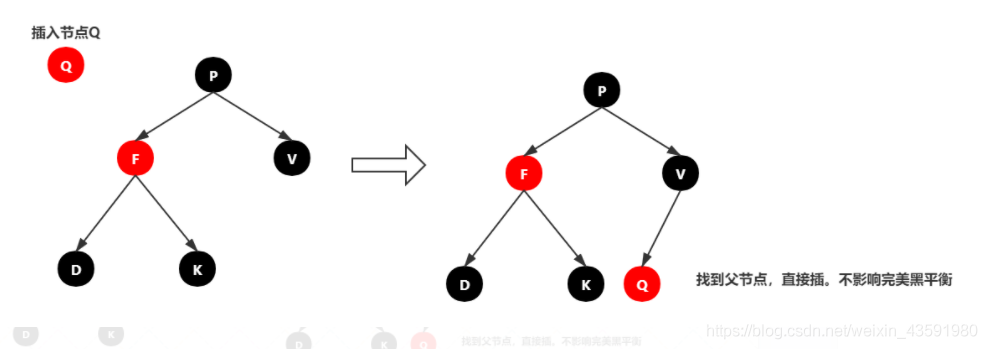
情景三：插入节点的父节点为黑色

由于插入的节点是红色的，当插入的节点的父节点为黑色的时候，并不会影响红黑树的平衡，直接插入即可，无需做自平衡。

情景四：插入节点的父节点为红色

再次回想下红黑树的性质2：根节点是黑色。如果插入节点的父节点为红节点，那么该父节点不可能为根节点，所以插入节点总是存在祖父节点。

这一点很关键，因为后续操作肯定需要祖父节点的参与。

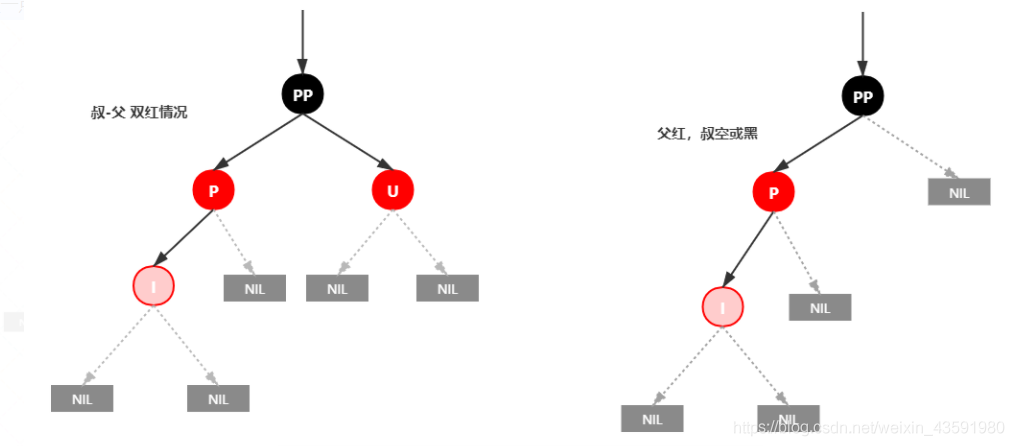
插入情景4.1：叔叔节点存在并且为红节点

依据红黑树性质四可知：红色节点不能相连 --> 祖父节点一定为黑节点

因为不可以同时存在两个相连的红节点，那么此时插入子树的红黑树层数的情况是：黑红红，显然最简单的方式是把其改变为：红黑红

处理：

将 P 和 U节点改为黑色
将 PP 改为红色
将 PP 设置为当前节点，进行后续处理

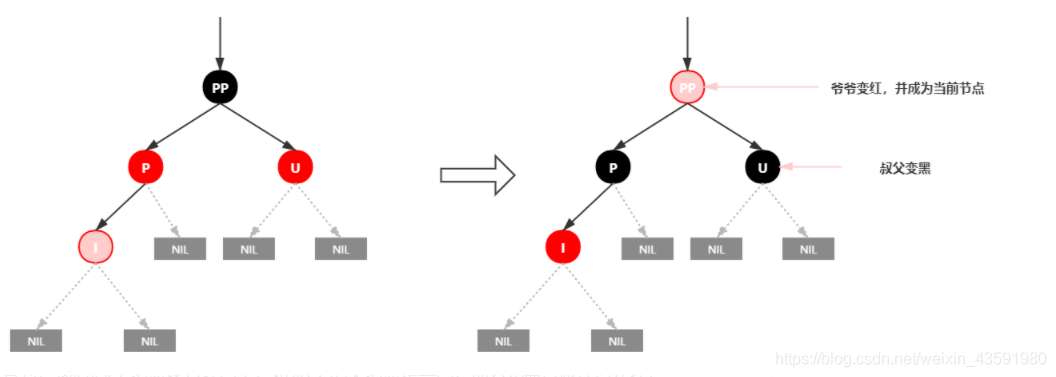
可以看到，我们把 PP 节点设置为红色了，如果 PP 的父节点为黑色，那么无需在做任何处理

但是如果 PP 的父节点是红色，则违反了红黑树性质了。所以需要将 PP 设置为当前节点，继续做插入操作自平衡处理，直到平衡为止。

插入情景4.2：叔叔节点不存在或者为黑节点，并且插入节点的父节点是祖父节点的左子节点

注意：单纯从插入前来看，叔叔节点非红即空（NIL节点），否则的话破坏了红黑树性质5，此路径就会比其他路劲多一个黑色节点

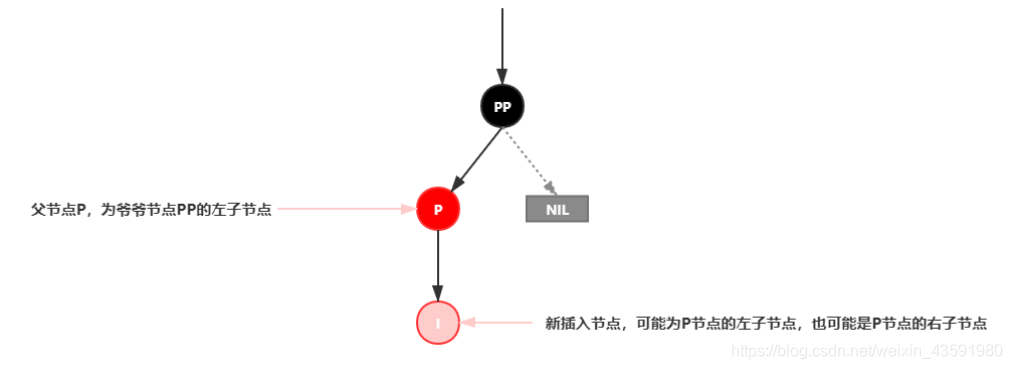
插入情景4.2.1：新插入节点，为其父节点的左子节点（LL 双红色情况）

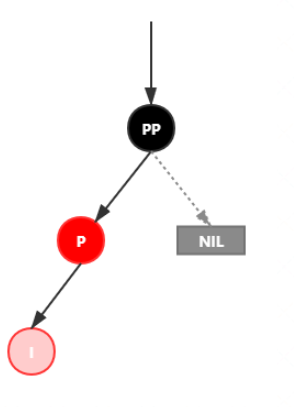
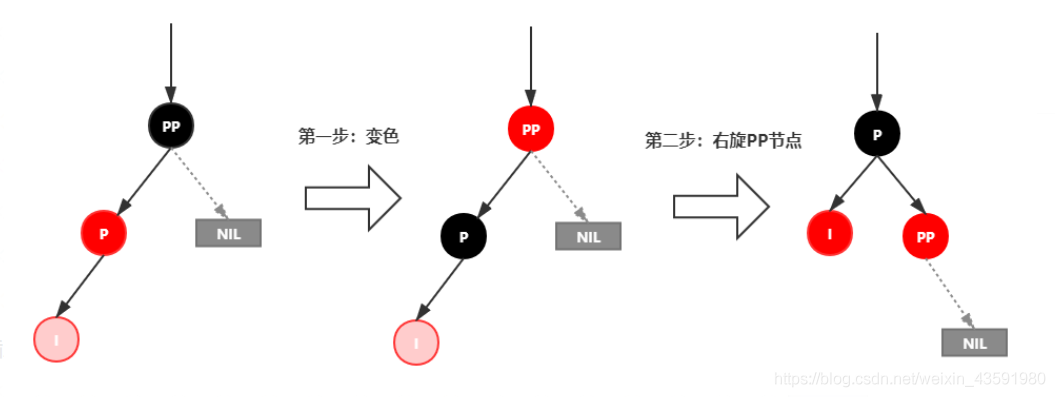
处理：

将 P 设置为黑色，将 PP 设置为红色
对 PP 节点进行右旋

插入情景4.2.2：新插入节点，为其父节点的右子节点（LR双红情况）

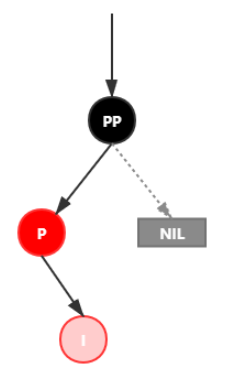
处理：

对 P 进行左旋
将 P 设置为当前节点，得到 LL 双红色情况
按照 LL 双红情况处理（1、变颜色 2、右旋 PP）

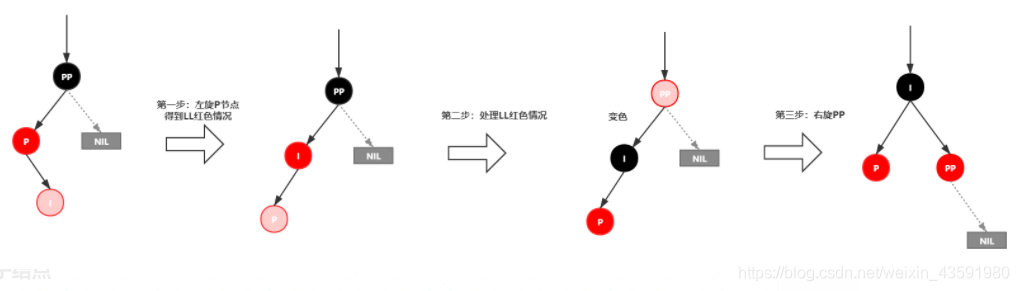
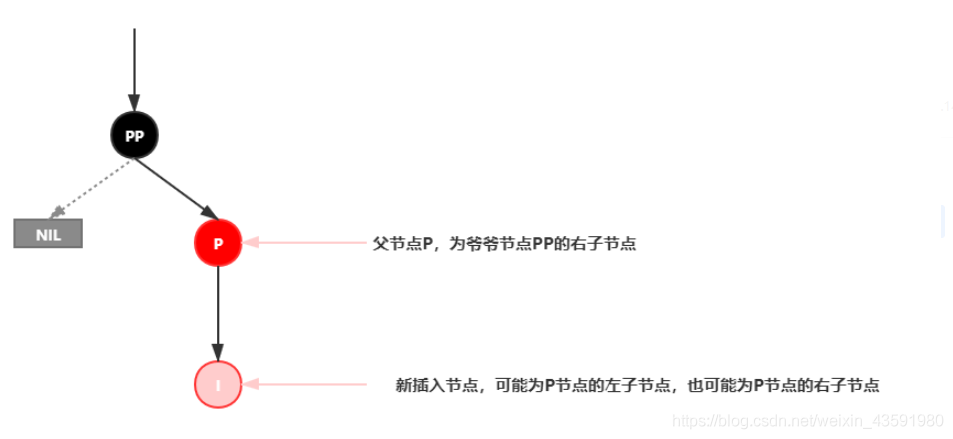
插入情景4.3：叔叔节点不存在或者为黑节点，并且插入节点的父节点是祖父节点的右子节点

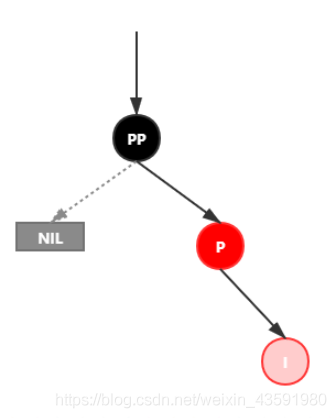
该情景对应情景4.2，只是方向反转，直接看图。

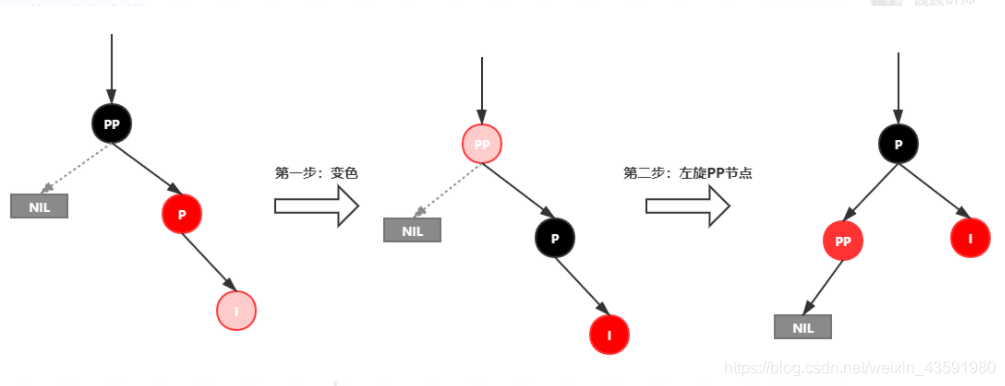
插入情景4.3.1：新插入节点，为其父节点的右子节点（RR 双红色情况）

处理：

变颜色：将 P 设置为黑色，将 PP 设置为红色
对 PP 节点进行左旋

插入情景4.3.2：新插入节点，为其父节点的左子节点（RL 双红情况）

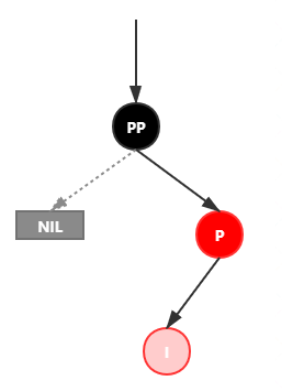
处理：

对 P 进行右旋
将 P 设置为当前节点，得到 RR 双红色情况
按照 RR 双红色情况处理（1、变颜色 2、左旋 PP）

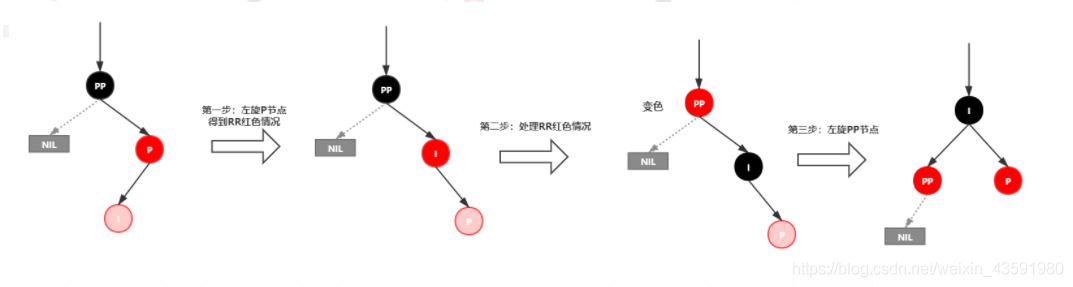
2.2、红黑树案例

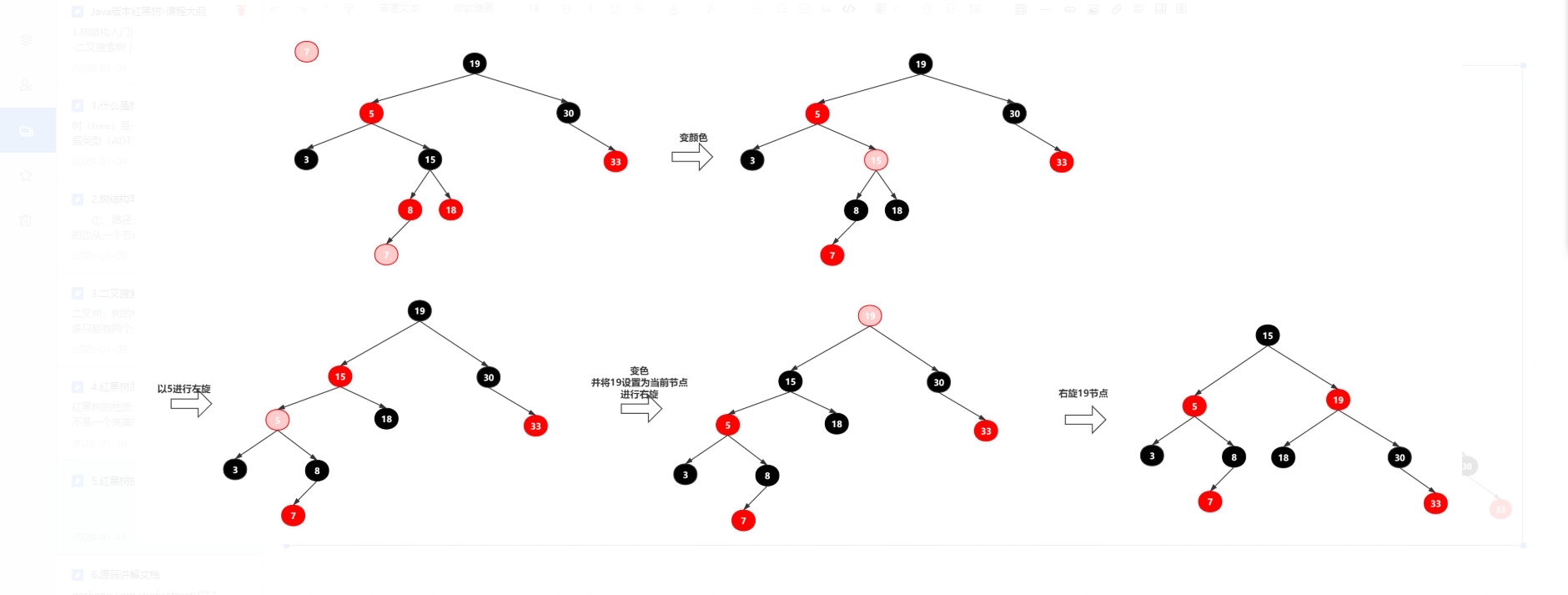
3、手写红黑树

创建 RBTree，定义颜色
创建 RBNode
辅助定义方法：parentOf(node)，isRed(node)，setRed(node)，setBlack(node)，inorderPrint()
左旋方法定义：leftRoate(node)
右旋方法定义：rightRoate(node)
公开插入接口方法定义：insert(K key,V value)
内部插入接口方法定义：insert(RBNode node)
修正插入导致红黑树失衡的方法定义：insertFixUp(RBNode node)
测试红黑树正确性

/**
 * @author wcc
 * @date 2021/12/15 20:10
 */
public class RBTree<K extends Comparable<K>, V> {

    /**
     * 创建 RBTree，定义颜色
     * 创建 RBNode
     * 辅助定义方法：parentOf(node)，isRed(node)，setRed(node)，setBlack(node)，inorderPrint()
     * 左旋方法定义：leftRoate(node)
     * 右旋方法定义：rightRoate(node)
     * 公开插入接口方法定义：insert(K key,V value)
     * 内部插入接口方法定义：insert(RBNode node)
     * 修正插入导致红黑树失衡的方法定义：insertFixUp(RBNode node)
     * 测试红黑树正确性
     */

    // 定义红黑树节点的颜色
    private static final boolean RED = true;
    private static final boolean BLACK = false;

    // 树根节点的引用
    private RBNode root;

    public RBNode getRoot() {
        return root;
    }

    /**
     * 获取当前节点的父节点
     * @param node
     */
    private RBNode parentOf(RBNode node){
        if(node != null){
            return node.parent;
        }
        return null;
    }

    /**
     * 判断节点是否为红色
     * @param node
     */
    private boolean isRed(RBNode node){
        if(node != null){
            return node.color == RED;
        }
        return false;
    }

    /**
     * 判断节点是否为黑色
     */
    private boolean isBlack(RBNode node){
        if(node != null){
            return node.color == BLACK;
        }
        return false;
    }

    /**
     * 设置节点为红色
     * @param node
     */
    private void setRed(RBNode node){
        if(node != null){
            node.color = RED;
        }
    }

    /**
     * 设置节点为黑色
     * @param node
     */
    private void setBlack(RBNode node){
        if(node != null){
            node.color = BLACK;
        }
    }

    /**
     * 二叉树的中序遍历
     */
    public void inorderPrint(){
        inorderPrint(this.root);
    }

    /**
     * 公开的插入方法
     * @param key
     * @param value
     */
    public void insert(K key, V value){
        // 创建新的节点，注意，新结点一定是红色
        RBNode node = new RBNode();
        node.setKey(key);
        node.setValue(value);
        node.setColor(RED);
        insert(node);
    }

    private void insert(RBNode node){
        // 第一步：查找当前node的父节点
        RBNode parent = null;
        RBNode x = this.root;
        int compare = -1; // 用于比较当前节点和node的值，确定循环的子树位置

        // 循环进行查找，当循环结束，x为空，然后parent为为要插入节点的父节点
        while (x != null){
            parent = x; // 将x赋值给parent
            // compare > 0，说明node.key 大于 x.key，需要到x的右子树进行查找
            // compare == 0，说明node.key 等于 x.key，说明需要进行替换操作
            // compare < 0，说明node.key 小于 x.key，需要到x的左子树进行查找
            compare = node.key.compareTo(x.key);
            if(compare > 0){
                x = x.right;
            }else if(compare == 0){
                x.setValue(node.getValue());
                return;
            }else{
                x = x.left;
            }
        }
        // 设置node的父节点
        node.parent = parent;
        if(parent != null){
            // 这里注意，需要根据compare的值来判断node是parent的子树类型
            if(compare > 0){ // 说明node应该位于parent的右子树
                parent.right = node;
            }
            if(compare < 0){ // 说明node应该位于parent的左子树
                parent.left = node;
            }
        }else{ // 说明当前红黑树没有节点，即把node设置为根节点
            this.root = node;
            node.setParent(null);
        }

        // 插入之后，可能会破坏红黑树的平衡性，需要对当前红黑树进行调整平衡操作
        // 注意，这里以插入节点为当前节点开始调整平衡
        insertFixUp(node);
    }

    /**
     * 插入后修复红黑树平衡的方法：
     *          |--- 情景1：红黑树为空树，将根节点染色为黑色
     *          |--- 情景2：插入节点的key已经存在，不需要处理
     *          |--- 情景3：插入节点的父节点为黑色，因为你所插入的路径，黑色节点的高度没有变化，红黑树依然平衡，不需要处理
     *
     *          情景4：需要咱们自己去处理：
     *          |--- 情景4：插入节点的父节点为红色
     *                 |--- 情景4.1：叔叔节点存在，并且为红色（父-叔 双红）
     *                              将父节点和叔叔染色为黑色，将祖父染色为红色，并且再以祖父节点为当前节点，进行下一轮处理
     *                 |--- 情景4.2：叔叔节点不存在，或者为黑色，父节点为祖父节点的左子树
     *                        |--- 情景4.2.1：插入节点为其父节点的左子节点（LL 双红情况）
     *                                       将父节点染色为黑色，祖父节点染色为红色，然后以爷爷节点右旋，就完成了
     *                        |--- 情景4.2.2：插入节点为其父节点的右子节点（LR 双红情况）
     *                                       以父节点进行一次左旋，得到LL双红情景（4.2.1情景），然后指定父节点为当前节点进行下一轮操作
     *                 |---  情景4.3：叔叔节点不存在，或者为黑色，父节点为祖父节点的右子树
     *                        |--- 情景4.3.1：插入节点为其父节点的右子节点（RR 双红情况）
     *                                       将父节点染色为黑色，祖父节点染色为红色，然后以祖父节点进行左旋，就完成了
     *                        |--- 情景4.3.2：插入节点为其父节点的左子节点（RL 双红情况）
     *                                       以父节点进行一次右旋，得到RR 双红情景（4.3.1情景），然后指定父节点为当前节点进行下一轮操作
     */
    private void insertFixUp(RBNode node){
        this.root.setColor(BLACK);
        RBNode parent = parentOf(node); // 父节点
        RBNode gparent = parentOf(parent); // 祖父节点

        // 情景4：插入节点的父节点为红色
        if(parent != null && isRed(parent)){
            // 注意，如果父节点存在，那么一定存在祖父节点，因为根节点不可能为红色
            RBNode uncle = null; // 叔叔节点
            if(parent == gparent.left){ // 父节点为祖父节点的左子树
                // 所以这里不需要判断祖父节点是否为空，因为一定不为空
                uncle = gparent.right;
                // 情景4.1：叔叔节点存在，并且为红色（父-叔 双红）
                if(uncle != null && isRed(uncle)){
                    // 将父节点和叔叔染色为黑色，将祖父染色为红色，并且再以祖父节点为当前节点，进行下一轮处理
                    setBlack(parent);
                    setBlack(uncle);
                    setRed(gparent);
                    node = gparent;
                    insertFixUp(node);
                    return;
                }

                // 情景4.2：叔叔节点不存在，或者为黑色
                if(uncle == null || isBlack(uncle)){
                    // 情景4.2.1：插入节点为其父节点的左子节点（LL 双红情况）
                    // 将父节点染色为黑色，祖父节点染色为红色，然后以爷爷节点右旋，就完成了
                    if(node == parent.left){
                        setBlack(parent);
                        setRed(gparent);
                        rightRotate(gparent);
                        return;
                    }else{ // 情景4.2.2：插入节点为其父节点的右子节点（LR 双红情况）
                        // 以父节点进行一次左旋，得到LL双红情景（4.2.1情景），然后指定父节点为当前节点进行下一轮操作
                        leftRoate(parent);
                        insertFixUp(parent);
                        return;
                    }
                }
            }else{ // 父节点为祖父节点的右子节点
                // 所以这里不需要判断祖父节点是否为空，因为一定不为空
                uncle = gparent.left;
                // 情景4.1：叔叔节点存在，并且为红色（父-叔 双红）
                if(uncle != null && isRed(uncle)){
                    // 将父节点和叔叔染色为黑色，将祖父染色为红色，并且再以祖父节点为当前节点，进行下一轮处理
                    setBlack(parent);
                    setBlack(uncle);
                    setRed(gparent);
                    insertFixUp(gparent);
                    return;
                }

                // 情景4.3：叔叔节点不存在，或者为黑色，父节点为祖父节点的右子树
                if(uncle == null || isBlack(uncle)){
                    // 情景4.3.1：插入节点为其父节点的右子节点（RR 双红情况）
                    if(node == parent.right){
                        // 将父节点染色为黑色，祖父节点染色为红色，然后以祖父节点进行左旋，就完成了
                        setBlack(parent);
                        setRed(gparent);
                        leftRoate(gparent);
                        return;
                    }else{ // 情景4.3.2：插入节点为其父节点的左子节点（RL 双红情况）
                        // 以父节点进行一次右旋，得到RR 双红情景（4.3.1情景），然后指定父节点为当前节点进行下一轮操作
                        rightRotate(parent);
                        insertFixUp(parent);
                        return;
                    }
                }
            }
        }
    }

    /**
     * 左旋方法
     * 左旋示意图：左旋x节点
     *   p                   p
     *   |                   |
     *   x                   y
     *  / \      ---->      / \
     * lx  y               x   ry
     *    / \             / \
     *   ly  ry          lx  ly
     *
     * 首先分析一下左旋的时候都做了什么事情？
     * 1.将y的左子节点的父节点更新为x，并将x的右子节点指向y的左子节点（ly）
     * 2.当x的父节点不为空的时候（即x节点不为根节点），更新y的父节点为x的父节点，并将x的父节点指定子树（当前x 子树位置）指定为 y
     * 3.将x的父节点更新为y，将y的左子节点更新为x
     */
    private void leftRoate(RBNode x){
        RBNode y = x.right; // 获取旋转节点的右子节点
        // 1.将y的左子节点的父节点更新为x（ly）
        if(y.left != null){
            y.left.parent = x;
        }
        // 并将x的右子节点指向y的左子节点（ly）不管y的左子节点是否为空
        x.right = y.left;

        // 2.当x的父节点不为空的时候（即x不为根节点），更新y的父节点为x的父节点，并将x的父节点指定子树（当前x的子树位置）指定为y
        if(x.parent != null){
            // 注意这里，无论x的父节点是否为空，都要更新y的父节点为x的父节点
            y.parent = x.parent;
            if(x == x.parent.left){
                x.parent.left = y;
            }else{
                x.parent.right = y;
            }
        }else{ // 说明x节点是根节点，此时需要更新y为根节点
            this.root = y;
            // 注意，这一步一定不能忘
            y.parent = null;
        }

        // 3.将x的父节点更新为y，将y的左子节点更新为x
        x.parent = y;
        y.left = x;
    }

    /**
     * 右旋方法
     * 右旋示意图：右旋y节点
     *
     *     p                       p
     *     |                       |
     *     y                       x
     *    / \          ---->      / \
     *   x   ry                  lx  y
     *  / \                         / \
     * lx  ly                      ly  ry
     *
     * 右旋都做了哪些事？
     * 1.将y的的左子节点指向x的右子节点，并且更新x的右子节点的父节点为y(ly)
     * 2.当y的父节点不为空的时候（即y不是根节点），更新x的父节点为y的父节点，更新y的父节点的指定子节点（y当前的位置）为x
     * 3.更新y的父节点为x，更新x的右子节点为y
     */
    private void rightRotate(RBNode y){
        RBNode x = y.left;
        // 1.将y的的左子节点指向x的右子节点
        if(x.right != null){
            x.right.parent = y;
        }
        // 并且更新x的右子节点的父节点为y(ly)，无论x的右子节点是否为空
        y.left = x.right;

        // 2.当y的父节点不为空的时候（即y不是根节点），更新x的父节点为y的父节点，更新y的父节点的指定子节点（y当前的位置）为x
        if(y.parent != null){
            x.parent = y.parent;
            if(y.parent.left == y){
                y.parent.left = x;
            }else{
                y.parent.right = x;
            }
        }else{ // 说明x节点是根节点，此时需要更新x为根节点
            this.root = x;
            x.parent = null;
        }

        // 3.更新y的父节点为x，更新x的右子节点为y
        y.parent = x;
        x.right = y;
    }

    private void inorderPrint(RBNode root){
        if(root.left != null){
            inorderPrint(root.left);
        }
        System.out.print(root.key + "  ");
        if(root.right != null){
            inorderPrint(root.right);
        }
    }

    static class RBNode<K extends Comparable<K>, V>{
        private RBNode parent; // 父节点
        private RBNode left; // 左节点
        private RBNode right; // 右节点
        private boolean color; // 节点颜色
        private K key;
        private V value;

        public RBNode(){}

        public RBNode(RBNode parent, RBNode left, RBNode right, boolean color, K key, V value) {
            this.parent = parent;
            this.left = left;
            this.right = right;
            this.color = color;
            this.key = key;
            this.value = value;
        }

        public RBNode getParent() {
            return parent;
        }

        public void setParent(RBNode parent) {
            this.parent = parent;
        }

        public RBNode getLeft() {
            return left;
        }

        public void setLeft(RBNode left) {
            this.left = left;
        }

        public RBNode getRight() {
            return right;
        }

        public void setRight(RBNode right) {
            this.right = right;
        }

        public boolean isColor() {
            return color;
        }

        public void setColor(boolean color) {
            this.color = color;
        }

        public K getKey() {
            return key;
        }

        public void setKey(K key) {
            this.key = key;
        }

        public V getValue() {
            return value;
        }

        public void setValue(V value) {
            this.value = value;
        }
    }
}

代码测试：

在网上找的一个打印红黑树的工具类：

/**
 * @author wcc
 * @date 2021/12/15 22:33
 */
public class RedAndBlackTreeOperation {
    /*
           树的结构示例：
              1
            /   \
          2       3
         / \     / \
        4   5   6   7
    */

    // 用于获得树的层数
    public static int getTreeDepth(RBTree.RBNode root) {
        return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight())));
    }


    private static void writeArray(RBTree.RBNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
        // 保证输入的树不为空
        if (currNode == null) return;
        // 先将当前节点保存到二维数组中
        res[rowIndex][columnIndex] = String.valueOf(currNode.getKey() + "-" + (currNode.isColor() ? "R" : "B") + "");

        // 计算当前位于树的第几层
        int currLevel = ((rowIndex + 1) / 2);
        // 若到了最后一层，则返回
        if (currLevel == treeDepth) return;
        // 计算当前行到下一行，每个元素之间的间隔（下一行的列索引与当前元素的列索引之间的间隔）
        int gap = treeDepth - currLevel - 1;

        // 对左儿子进行判断，若有左儿子，则记录相应的"/"与左儿子的值
        if (currNode.getLeft() != null) {
            res[rowIndex + 1][columnIndex - gap] = "/";
            writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
        }

        // 对右儿子进行判断，若有右儿子，则记录相应的"\"与右儿子的值
        if (currNode.getRight() != null) {
            res[rowIndex + 1][columnIndex + gap] = "\\";
            writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
        }
    }


    public static void show(RBTree.RBNode root) {
        if (root == null) System.out.println("EMPTY!");
        // 得到树的深度
        int treeDepth = getTreeDepth(root);

        // 最后一行的宽度为2的（n - 1）次方乘3，再加1
        // 作为整个二维数组的宽度
        int arrayHeight = treeDepth * 2 - 1;
        int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
        // 用一个字符串数组来存储每个位置应显示的元素
        String[][] res = new String[arrayHeight][arrayWidth];
        // 对数组进行初始化，默认为一个空格
        for (int i = 0; i < arrayHeight; i++) {
            for (int j = 0; j < arrayWidth; j++) {
                res[i][j] = " ";
            }
        }

        // 从根节点开始，递归处理整个树
        // res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0');
        writeArray(root, 0, arrayWidth / 2, res, treeDepth);

        // 此时，已经将所有需要显示的元素储存到了二维数组中，将其拼接并打印即可
        for (String[] line : res) {
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < line.length; i++) {
                sb.append(line[i]);
                if (line[i].length() > 1 && i <= line.length - 1) {
                    i += line[i].length() > 4 ? 2 : line[i].length() - 1;
                }
            }
            System.out.println(sb.toString());
        }
    }
}

测试：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    RBTree<Integer, Object> rbTree = new RBTree<>();
    while (true){
        System.out.println("请输入要插入的节点的key：");
        Integer key = Integer.parseInt(scanner.next());
        System.out.println();
        rbTree.insert(key,key);
        RedAndBlackTreeOperation.show(rbTree.root);
    }
}

测试结果如下：

请输入要插入的节点的key：
1

1-B
请输入要插入的节点的key：
2

   1-B 
    \  
     2-R
请输入要插入的节点的key：
3

   2-B 
  / \  
 1-R 3-R
请输入要插入的节点的key：
4

      2-B    
    /   \    
  1-B     3-B
           \ 
            4-R
请输入要插入的节点的key：
5

      2-B    
    /   \    
  1-B     4-B
         / \ 
        3-R 5-R
请输入要插入的节点的key：
6

            2-B          
         /     \         
      1-B         4-R    
                /   \    
              3-B     5-B
                       \ 
                        6-R
请输入要插入的节点的key：
7

            2-B          
         /     \         
      1-B         4-R    
                /   \    
              3-B     6-B
                     / \ 
                    5-R 7-R
请输入要插入的节点的key：
8

            4-B          
         /     \         
      2-R         6-R    
    /   \       /   \    
  1-B     3-B 5-B     7-B
                       \ 
                        8-R
请输入要插入的节点的key：
9

            4-B          
         /     \         
      2-R         6-R    
    /   \       /   \    
  1-B     3-B 5-B     8-B
                     / \ 
                    7-R 9-R
请输入要插入的节点的key：
10

                        4-B                      
                    /       \                    
                2-B             6-B              
             /     \         /     \             
          1-B         3-B 5-B         8-R        
                                    /   \        
                                  7-B     9-B    
                                           \     
                                            10-R 
请输入要插入的节点的key：
-1

                        4-B                      
                    /       \                    
                2-B             6-B              
             /     \         /     \             
          1-B         3-B 5-B         8-R        
        /                           /   \        
      -1-R                        7-B     9-B    
                                           \     
                                            10-R 
请输入要插入的节点的key：
-2

                        4-B                      
                    /       \                    
                2-B             6-B              
             /     \         /     \             
          -1-B        3-B 5-B         8-R        
        /   \                       /   \        
      -2-R    1-R                 7-B     9-B    
                                           \     
                                            10-R 
请输入要插入的节点的key：
-3

                        4-B                      
                    /       \                    
                2-B             6-B              
             /     \         /     \             
          -1-R        3-B 5-B         8-R        
        /   \                       /   \        
      -2-B    1-B                 7-B     9-B    
     /                                     \     
    -3-R                                    10-R 
请输入要插入的节点的key：
11

                        4-B                      
                    /       \                    
                2-B             6-B              
             /     \         /     \             
          -1-R        3-B 5-B         8-R        
        /   \                       /   \        
      -2-B    1-B                 7-B     10-B   
     /                                   / \     
    -3-R                                9-R 11-R 
请输入要插入的节点的key：
12

                        4-B                      
                    /       \                    
                2-B             8-B              
             /     \         /     \             
          -1-R        3-B 6-R         10-R       
        /   \           /   \       /   \        
      -2-B    1-B     5-B     7-B 9-B     11-B   
     /                                     \     
    -3-R                                    12-R

至此，手写红黑树已经完成了，虽然刚学挺麻烦感觉，其实仔细回想觉得思路也是很清晰的，只要好好理解，代码还是可以的！