[数据结构与算法]图的入门学习

数据结构物回顾

• 线性结构: 数组、链表、栈、队列、哈希表
• 树形结构: 二叉树、B树、堆、Trie(字典树)、哈夫曼树、并查集
• 图形结构

相关概念

图

• 图由顶点(vertex)和边(edge)组成，通常表示为G=(V,E)
• G表示一个图,V是顶点集,E是边集
• 顶点集V有穷且非空
• 任意两个顶点之间都可以用边来表示它们之间的关系，边集E可以是空的
  

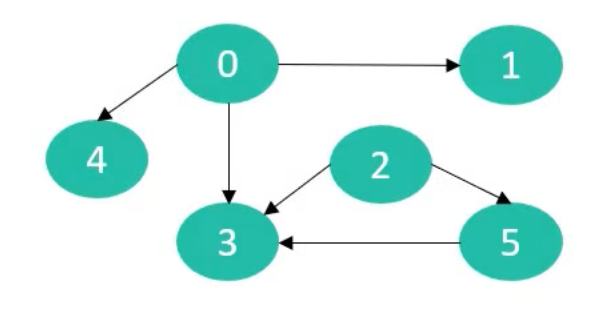
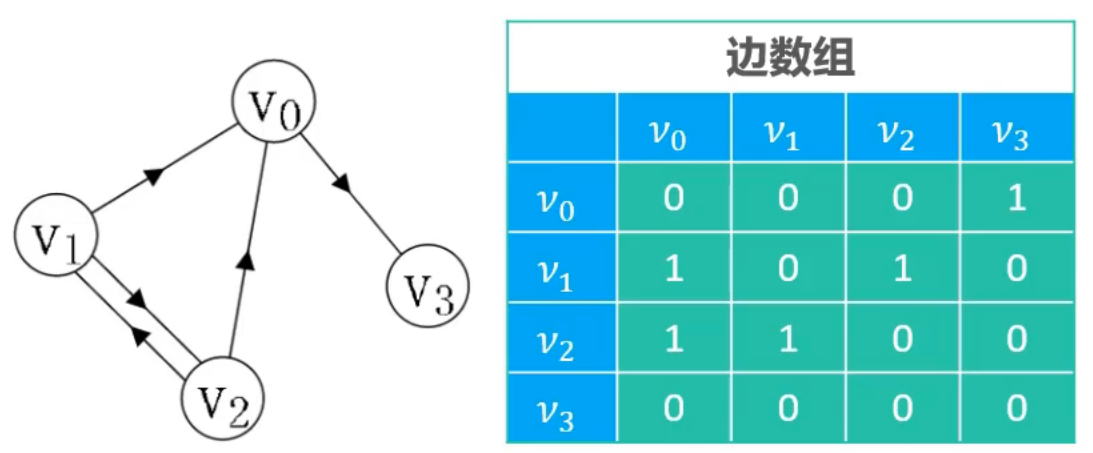
有向图

• 有向图的边是由明确方向的
  

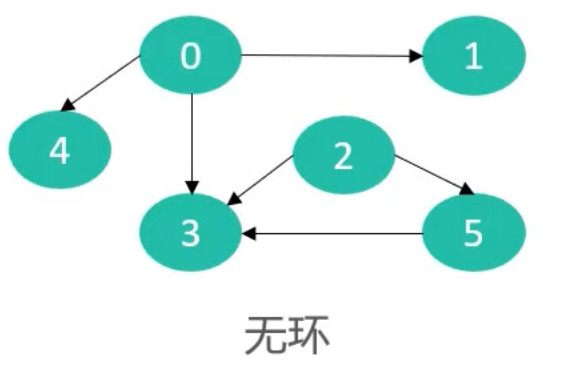
• 有向无环图(Directed Acyclic Graph 简称DAG)

• 如果一个有向图，丛任意顶点出发无法经过若干条边回到该顶点，那么它就是一个有向无环图
  

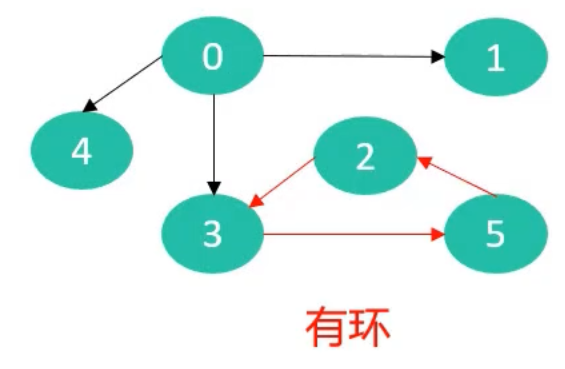
出度、入度

• 出度、入度适用于有向图
• 出度
  • 一个顶点的出度为x,是指有x条边以该顶点为起点
• 入度
  • 一个顶点的入度为x, 是指有x条边以该顶点为终点
    

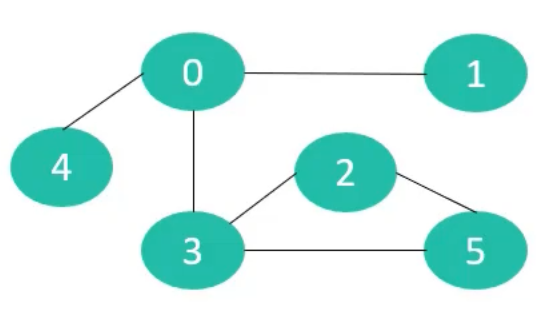
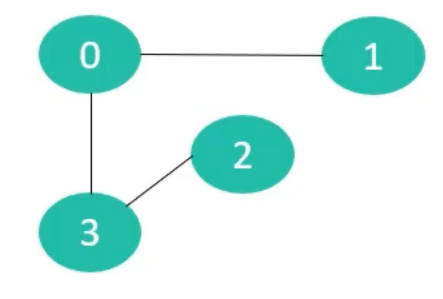
无向图

• 无向图的边是无方向的
  

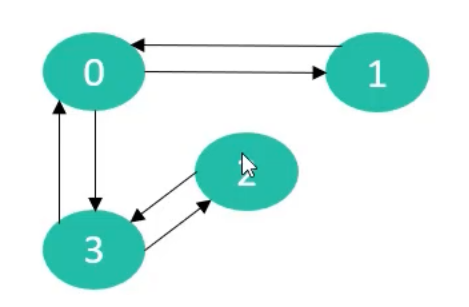
• 效果类似于下面的有向图
  

混合图

• 混合图的边可能是无向的，也可能是有向的
  

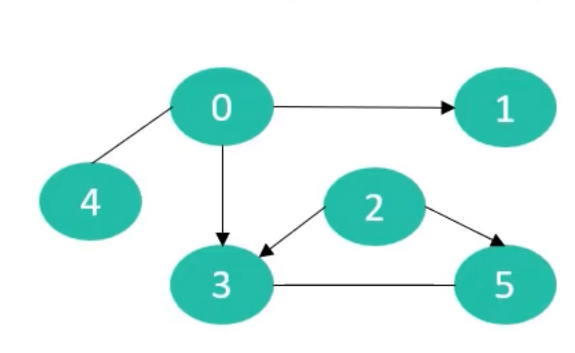
简单图、多重图

• 平行边
  • 在无向图中，关联一对顶点的无向边如果多余1条，则称这些边为平行边
  • 在有向图中，关联一对顶点的有向边如果多于1条，并且他们的方向相同，则称这些边为平行边
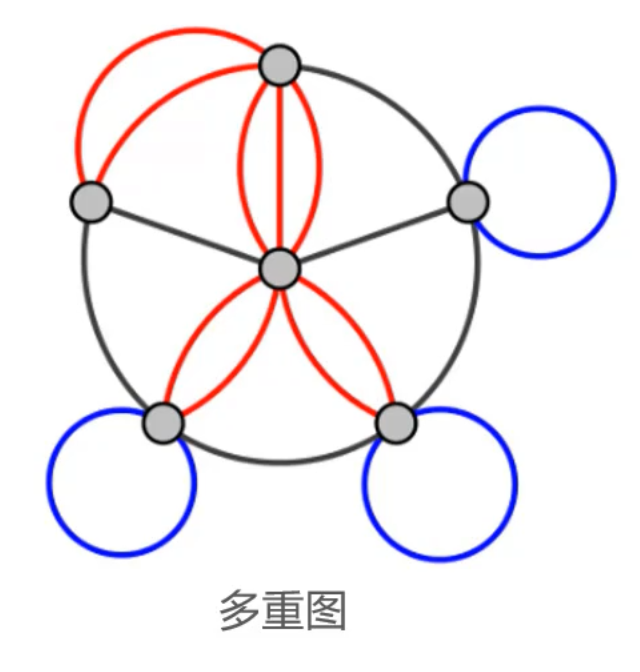
• 多重图
  • 有平行边或者自环的图
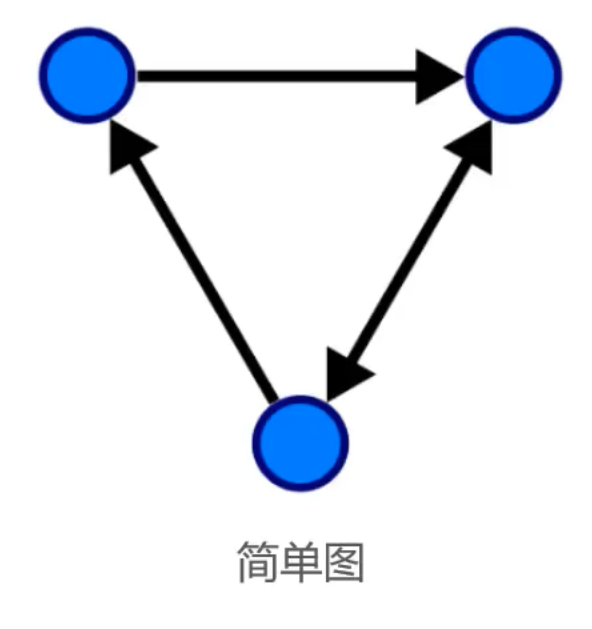
• 简单图
  • 既没有平行边也没有自环的图
    

无向完全图

• 无向完全图的任意两个顶点之间都存在边
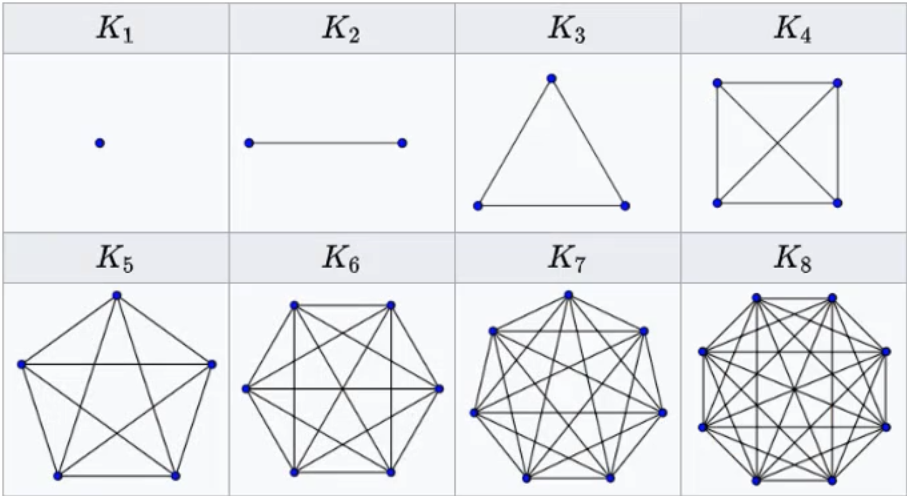
  • n个顶点的无向完全图有n(n-1)/2条边
    

有向完全图

• 有向完全图的任意两个顶点之间都存在方向相反的两条边

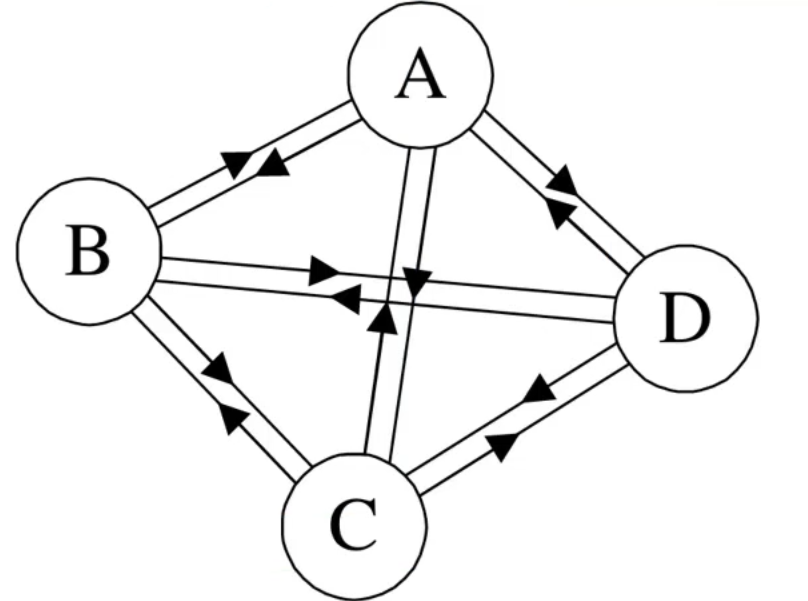
  • n个顶点的有向完全图有n(n-1)条边
    

• 稠密图: 边数接近于或等于完全图

• 稠密图: 边数远远少于完全图

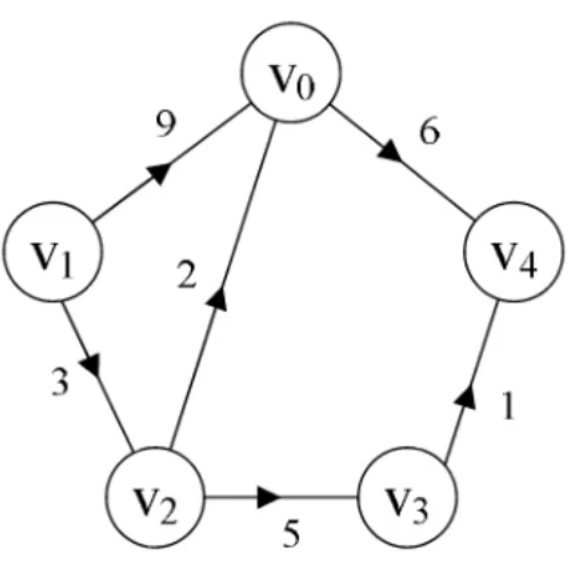
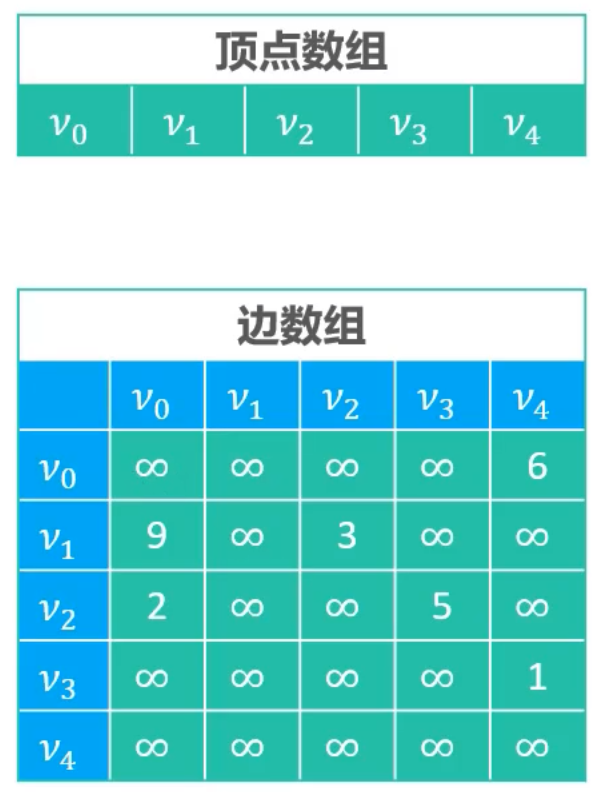
有权图

• 有权图的边可以拥有权值(Weight)
  

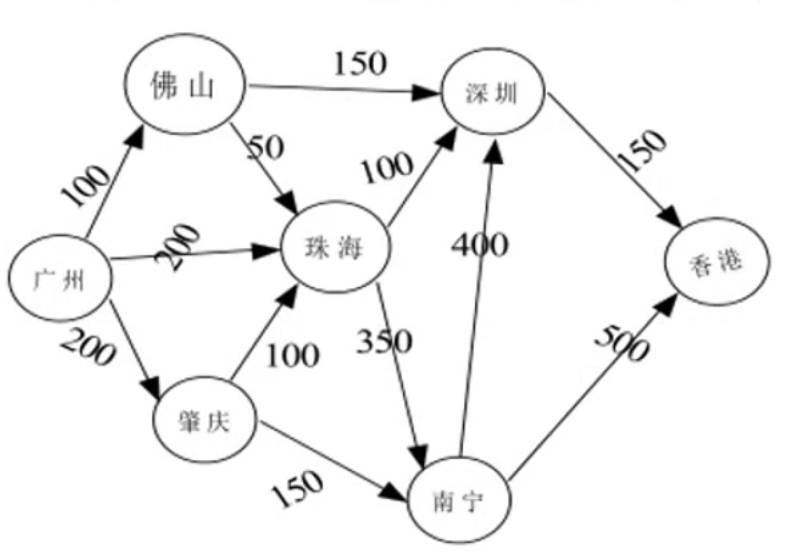
连通图

• 如果顶点x和y之间存在可相互抵达的路径(直接或间接的路径),则称x和y是连通的
• 如果无向图G中任意2个顶点都是连通的，则称G为连通图
  

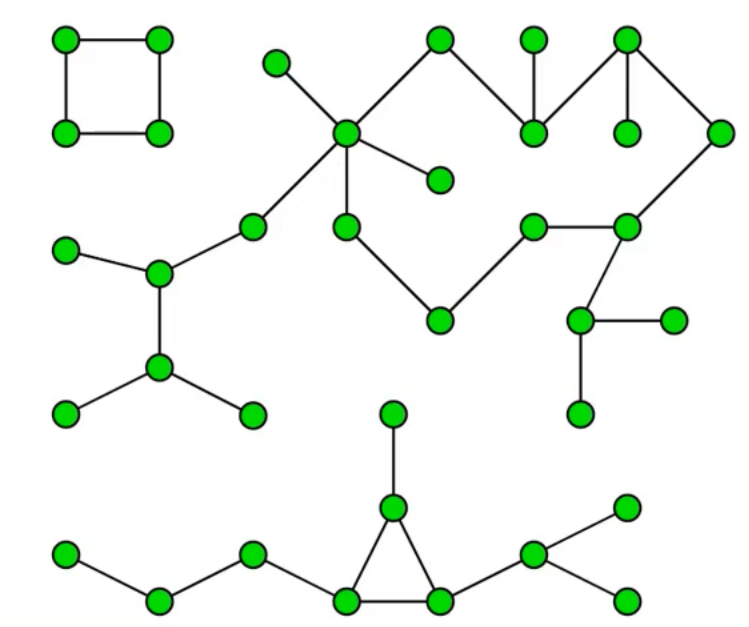
连通分量

• 连通分量； 无向图的极大连通子图
  • 连通图只有一个连通分量，即其自身;非连通的无向图有多个连通分量
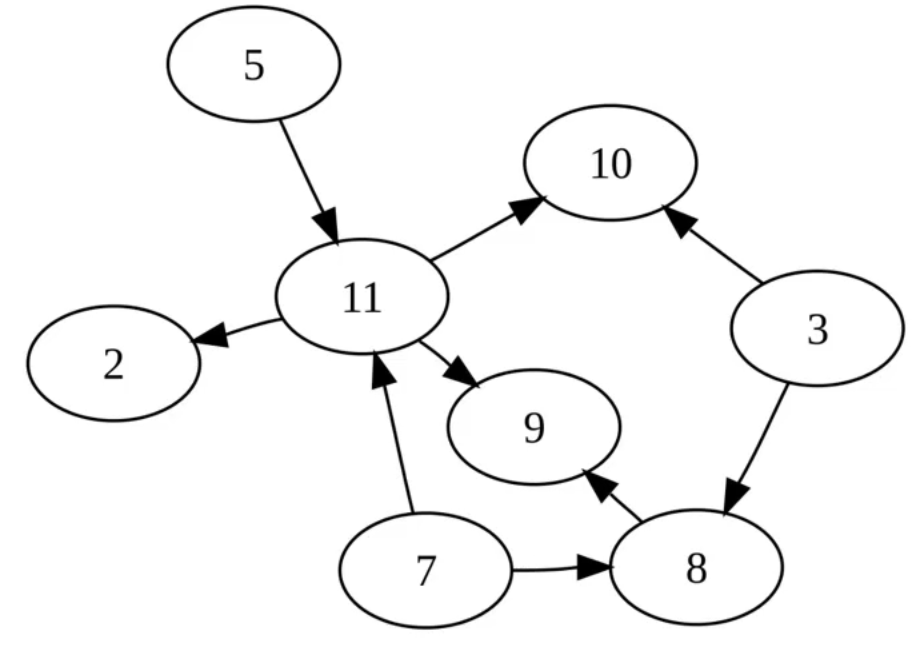
• 下面的无向图有3个连通分量
  

强连通图

• 如果有向图G中任意2个定点都是连通的，则称G为强连通图
  

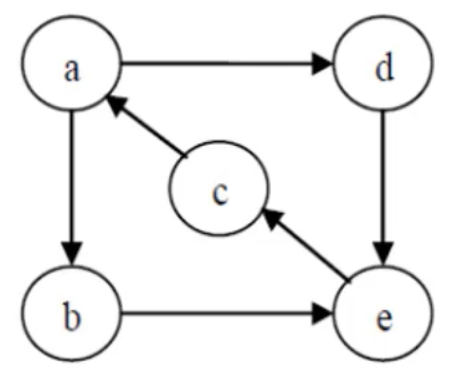
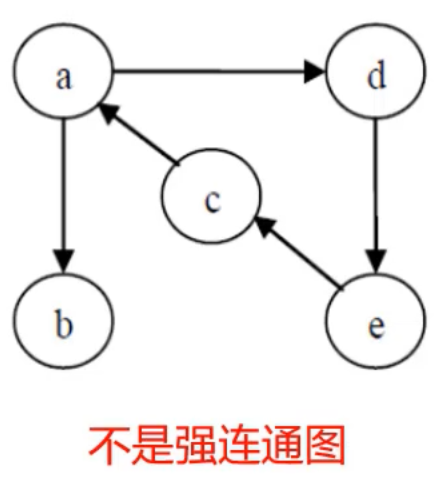
强连通分量

• 强连通分量: 有向图的极大强连通子图
  • 强连通图只有一个强连通分量，及其自身;非强连通的有向图有多个强连通分量
    

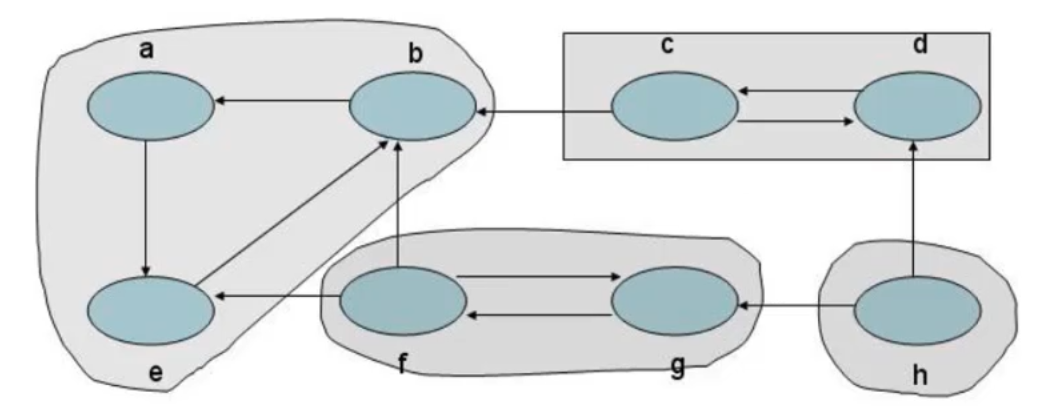
图的实现方案

• 图有2中常见的实现方案
  • 邻接矩阵
  • 邻接表

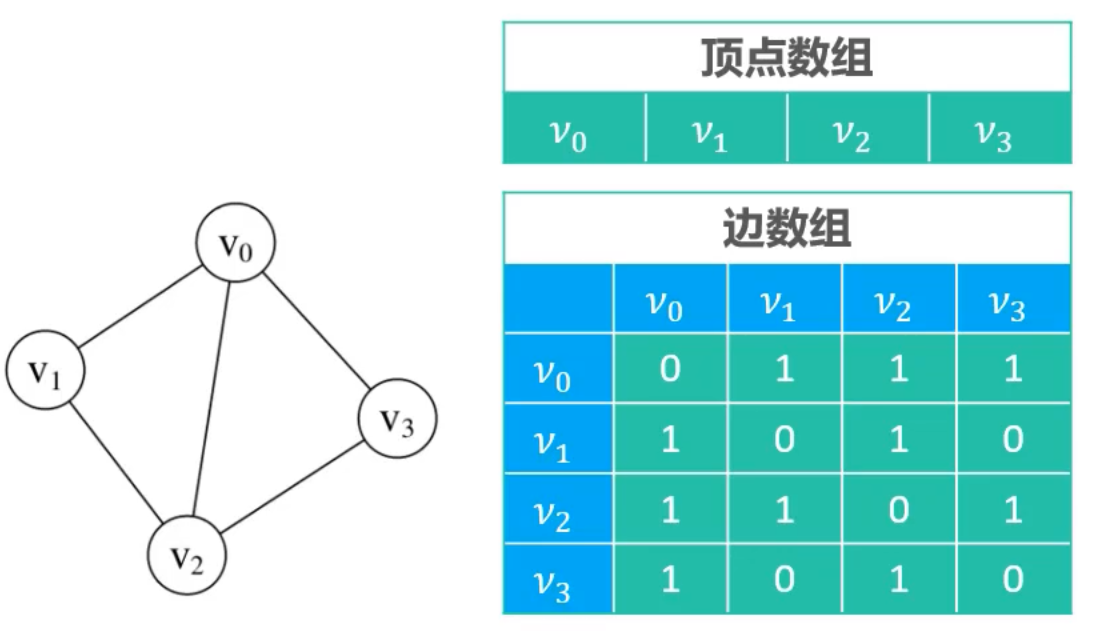
邻接矩阵

• 邻接矩阵的存储方式
  • 一维数组存放顶点信息
  • 二维数组存放边信息
• 邻接矩阵比较适合稠密图
  • 不然会比较浪费内存

邻接矩阵 - 有权图

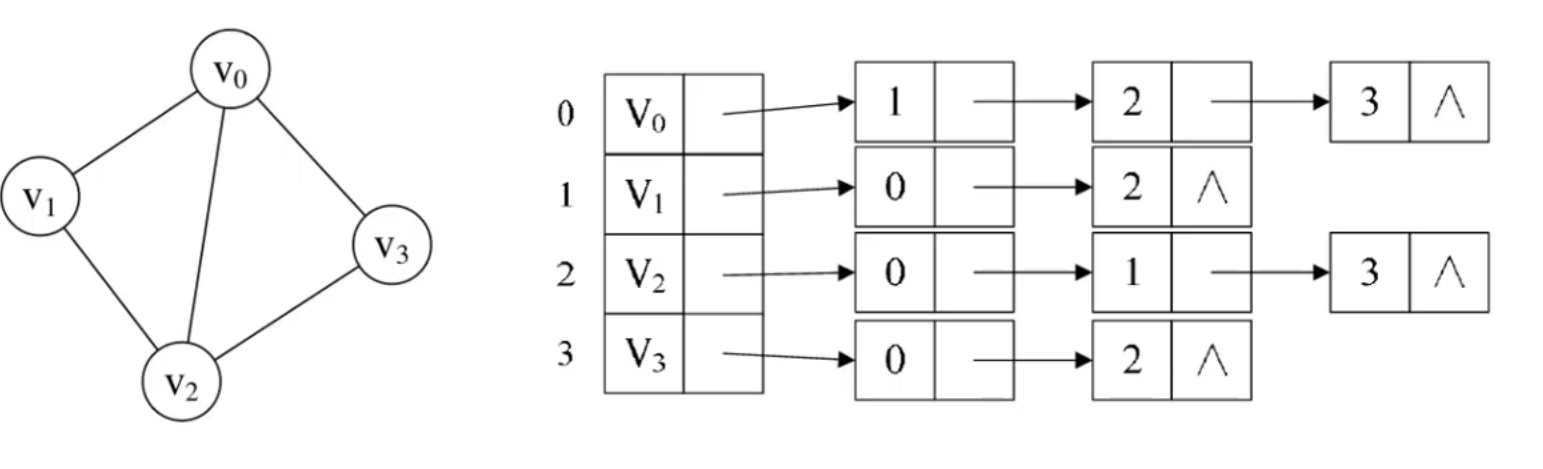
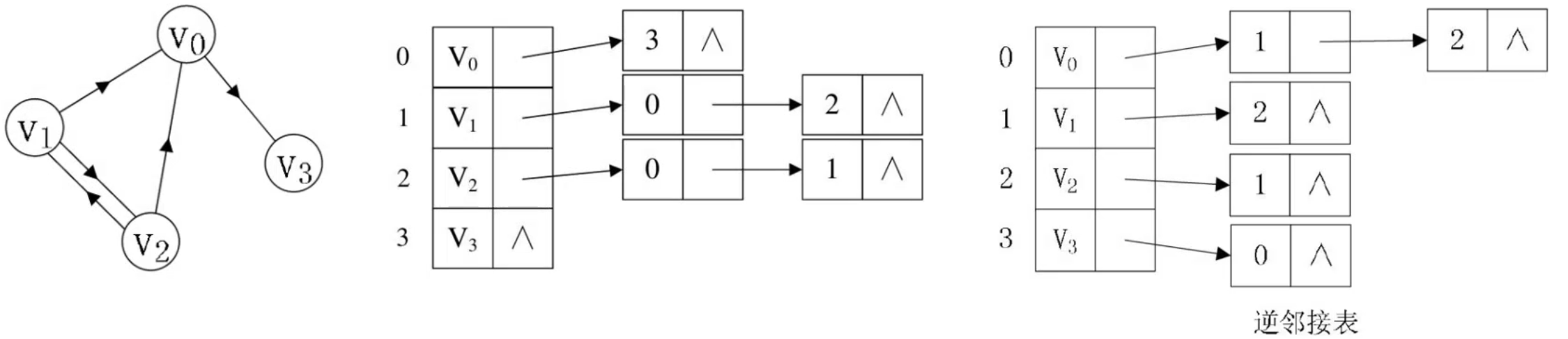
邻接表

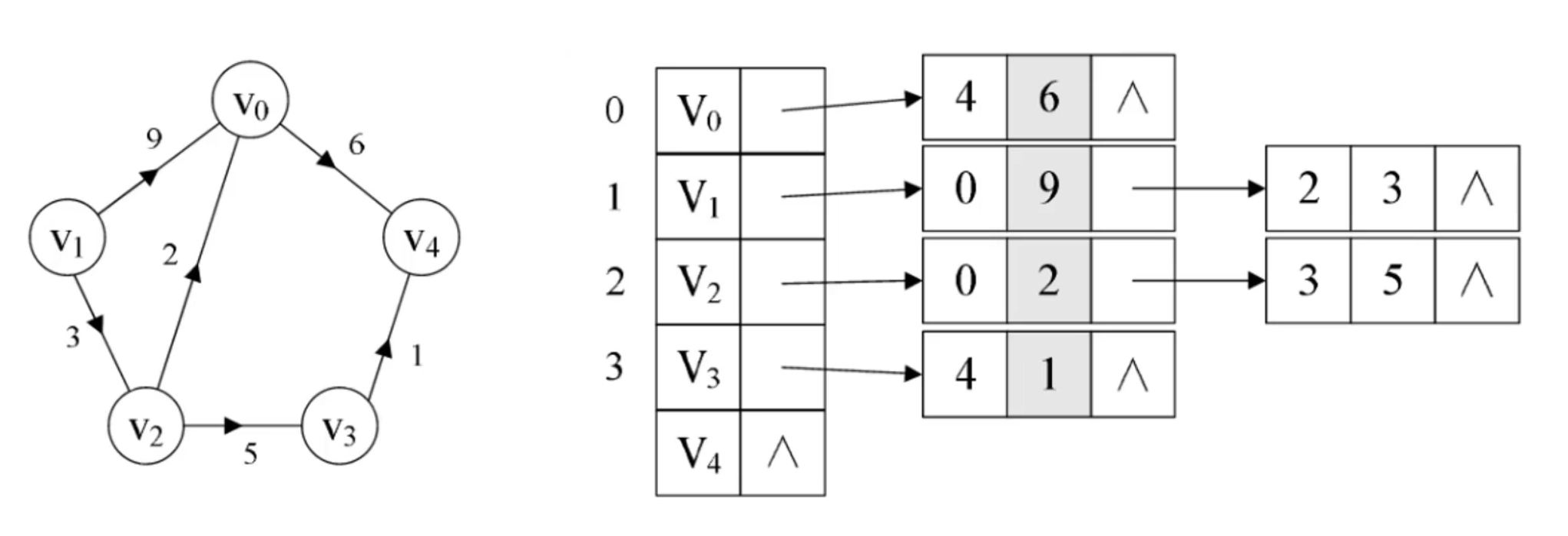
邻接表 - 有权图

实现图

Graph接口

public interface Graph<V, E> {

    /**
     * 打印边
     */
    void print();

    /**
     * 边的数量
     * @return
     */
    int edgeSize();

    /**
     * 顶点的数量
     * @return
     */
    int vertexSize();

    /**
     * 添加顶点
     * @param v
     */
    void addVertex(V v);

    /**
     * 添加边(无权值)
     * @param from
     * @param to
     */
    void addEdge(V from, V to);

    /**
     * 添加边(有权值)
     * @param from
     * @param to
     * @param weight
     */
    void addEdge(V from, V to, E weight);

    /**
     * 移除顶点
     * @param v
     */
    void removeVertex(V v);

    /**
     * 移除边
     * @param from
     * @param to
     */
    void removeEdge(V from, V to);

}

ListGraph类

public class ListGraph<V, E> implements Graph<V, E> {

    private Map<V, Vertex<V, E>> vertices = new HashMap<>();
    private Set<Edge<V, E>> edges = new HashSet<>();

    /**
     * 打印
     */
    @Override
    public void print() {
        //打印顶点
        vertices.forEach((v, vertex) -> {
            System.out.println(v);
            System.out.println("out-----------");
            System.out.println(vertex.outEdges);
            System.out.println("in------------");
            System.out.println(vertex.inEdges);
        });
        //打印边
        edges.forEach(edge -> System.out.println(edge));
    }

    @Override
    public int edgeSize() {
        return edges.size();
    }

    @Override
    public int vertexSize() {
        return vertices.size();
    }

    @Override
    public void addVertex(V v) {
        if (vertices.containsKey(v)) {
            return;
        }
        //添加顶点
        vertices.put(v, new Vertex<>(v));

    }

    @Override
    public void addEdge(V from, V to) {
        addEdge(from, to, null);
    }

    @Override
    public void addEdge(V from, V to, E weight) {
        Vertex<V, E> fromVertex = vertices.get(from);
        //如果map中不存在value=from的顶点,则创建并放到map中
        if (fromVertex == null) {
            fromVertex = new Vertex<>(from);
            vertices.put(from, fromVertex);
        }

        //如果map中不存在value=to的顶点,则创建并放到map中
        Vertex<V, E> toVertex = vertices.get(to);
        if (toVertex == null) {
            toVertex = new Vertex<>(to);
            vertices.put(to, toVertex);
        }

        //根据两个顶点创建边
        Edge<V, E> edge = new Edge<>(fromVertex, toVertex);
        //赋权值
        edge.weight = weight;

        //如果edge这条边已存在,就删除edge这条边,在from顶点的outEdges集合中删掉这条边,在to顶点的inEdges集合中删除这条边,直接删除原来的边,重新添加新的边,因为权值可能更新了。
        if (fromVertex.outEdges.remove(edge)) {
            toVertex.inEdges.remove(edge);
        }
        //再次把边添加到两个顶点的两个集合中。
        fromVertex.outEdges.add(edge);
        toVertex.inEdges.add(edge);

        //将边添加到集合edges中
        edges.add(edge);
    }

    @Override
    public void removeVertex(V v) {
        Vertex<V, E> vertex = vertices.remove(v);
        //如果map中不存在value=v的顶点,直接返回
        if (vertex == null) {
            return;
        }

        //删除边集和Edges中的所有和顶点vertex相关的边
        for (Iterator<Edge<V, E>> iterator = vertex.outEdges.iterator(); iterator.hasNext();) {
            Edge<V, E> edge = iterator.next();
            edge.to.inEdges.remove(edge);
            iterator.remove();
            edges.remove(edge);
        }

        for (Iterator<Edge<V, E>> iterator = vertex.inEdges.iterator(); iterator.hasNext();) {
            Edge<V, E> edge = iterator.next();
            edge.from.outEdges.remove(edge);
            iterator.remove();
            edges.remove(edge);
        }
    }

    @Override
    public void removeEdge(V from, V to) {
        Vertex<V, E> fromVertex = vertices.get(from);
        //如果map中不存在value=from的顶点,则肯定也没有以from为顶点的边
        if (fromVertex == null) {
            return;
        }

        //如果map中不存在value=to的顶点,则肯定也没有以to为顶点的边
        Vertex<V, E> toVertex = vertices.get(to);
        if (toVertex == null) {
            return;
        }

        //根据两个顶点创建边
        Edge<V, E> edge = new Edge<>(fromVertex, toVertex);
        //删除对应的边
        if (fromVertex.outEdges.remove(edge)) {
            toVertex.inEdges.remove(edge);
            edges.remove(edge);
        }
    }

    /**
     * 顶点
     */
    private static class Vertex<V, E> {
        V value;
        Set<Edge<V, E>> inEdges = new HashSet<>();
        Set<Edge<V, E>> outEdges = new HashSet<>();

        public Vertex(V value) {
            this.value = value;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) {
                return true;
            }
            if (o == null || getClass() != o.getClass()) {
                return false;
            }
            Vertex<V, E> vertex = (Vertex<V, E>) o;
            return Objects.equals(value, vertex.value);
        }

        @Override
        public int hashCode() {
            return Objects.hash(value);
        }

        @Override
        public String toString() {
            return value == null ? "null" : value.toString();
        }
    }

    /**
     * 边
     */
    private static class Edge<V, E> {
        Vertex<V, E> from;
        Vertex<V, E> to;
        E weight;

        public Edge(Vertex<V, E> from, Vertex<V, E> to) {
            this.from = from;
            this.to = to;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) {
                return true;
            }
            if (o == null || getClass() != o.getClass()) {
                return false;
            }
            Edge<V, E> edge = (Edge<V, E>) o;
            return Objects.equals(from, edge.from) && Objects.equals(to, edge.to);
        }

        @Override
        public int hashCode() {
            return Objects.hash(from, to);
        }

        @Override
        public String toString() {
            return "Edge{" +
                    "from=" + from +
                    ", to=" + to +
                    ", weight=" + weight +
                    '}';
        }
    }

}

测试类

public class Main {

    public static void main(String[] args) {
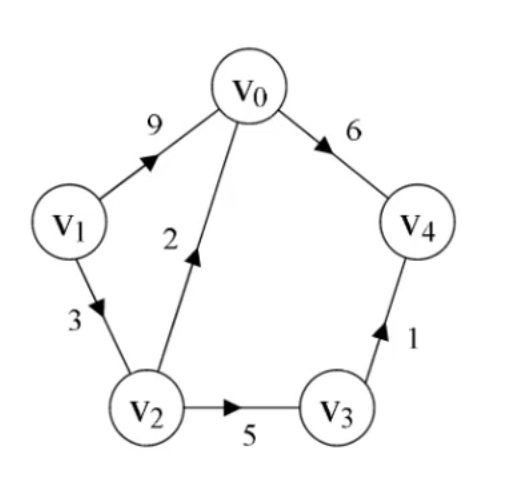
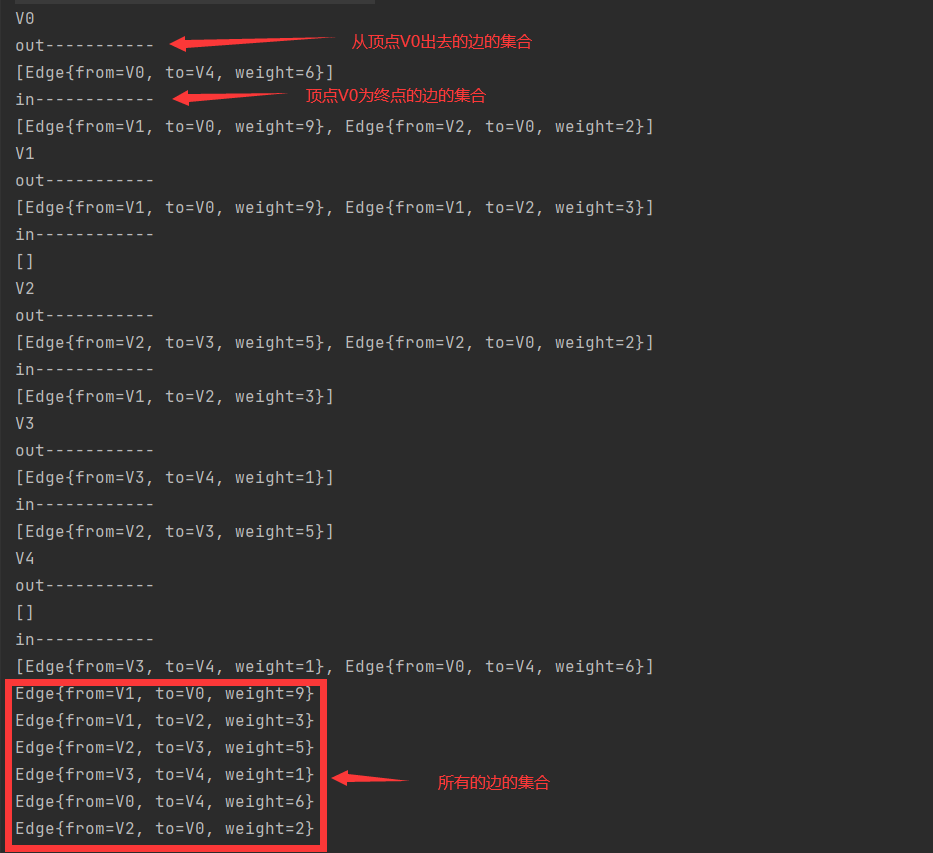
        Graph<String, Integer> graph = new ListGraph<>();
        graph.addEdge("V1", "V0", 9);
        graph.addEdge("V1", "V2", 3);
        graph.addEdge("V2", "V0", 2);
        graph.addEdge("V2", "V3", 5);
        graph.addEdge("V3", "V4", 1);
        graph.addEdge("V0", "V4", 6);

        //测试删除边
        //graph.removeEdge("V0", "V4");
        //测试删除顶点V0
        graph.removeVertex("V0");
        graph.print();
    }

}

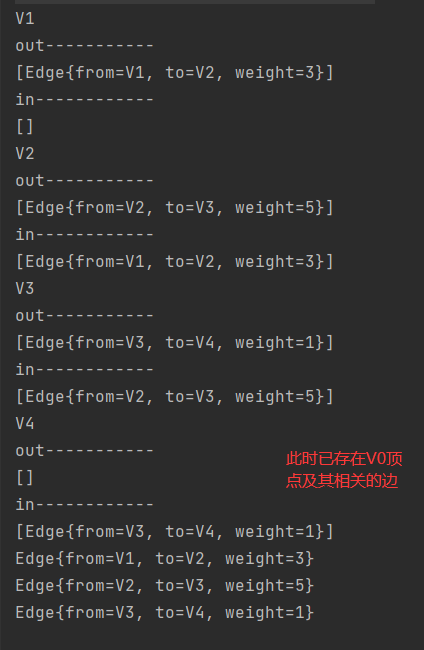
测试生成图

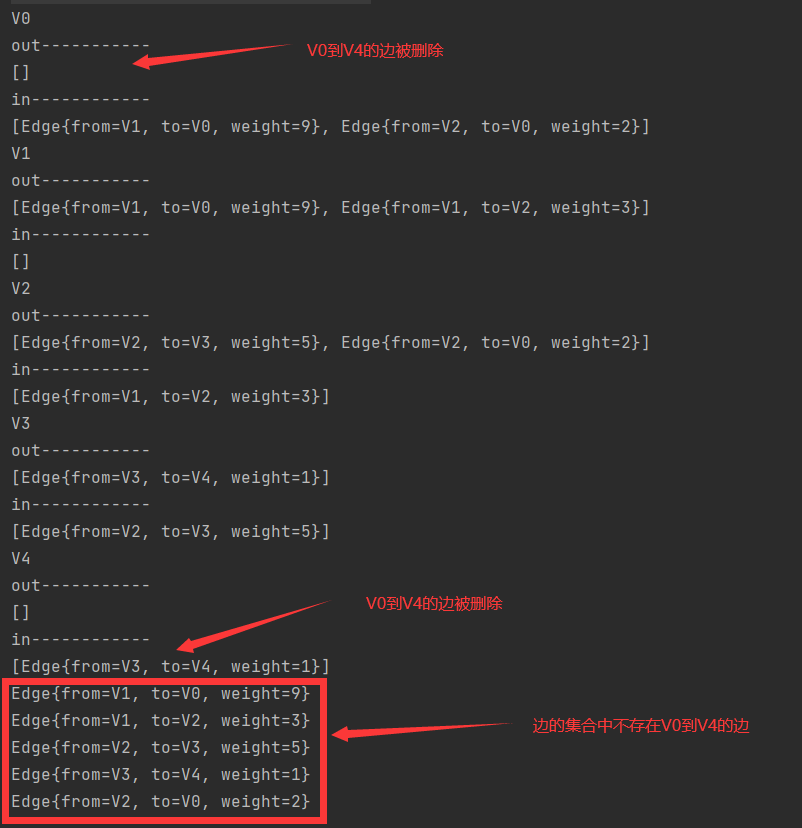
测试删除边

• 删除了顶点V0到顶点V4的边
  

测试删除顶点

• 测试删除V0顶点及其相关的边