开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【解题报告】《LeetCode零基础指南》(第七讲) 贪心 - Java -> 正文阅读

[数据结构与算法]【解题报告】《LeetCode零基础指南》(第七讲) 贪心 - Java

在这里插入图片描述

一、1913. 两个数对之间的最大乘积差

1.题目

1913. 两个数对之间的最大乘积差

两个数对 (a, b) 和 (c, d) 之间的乘积差定义为 (a * b) - (c * d) 。
例如，(5, 6) 和 (2, 7) 之间的乘积差是 (5 * 6) - (2 * 7) = 16 。
给你一个整数数组 nums ，选出四个不同的下标 w、x、y 和 z ，使数对 (nums[w], nums[x]) 和 (nums[y], nums[z]) 之间的乘积差取到最大值。
返回以这种方式取得的乘积差中的最大值。

2.分析

要使得乘积差尽可能大，则 $(a ? b)$ 尽可能大， $(c ? d)$ 尽可能小。
所以对数组排序后， $a, b$ 取最大的两个值， $c, d$ 取最小的两个值即可。

3.代码

class Solution {
    public int maxProductDifference(int[] nums) {
        Arrays.sort(nums);
        int length = nums.length;
        return (nums[length - 1] * nums[length - 2]) - (nums[0] * nums[1]);
    }
}

在这里插入图片描述

二、976. 三角形的最大周长

1.题目

976. 三角形的最大周长

给定由一些正数（代表长度）组成的数组 A，返回由其中三个长度组成的、面积不为零的三角形的最大周长。
如果不能形成任何面积不为零的三角形，返回 0。

2.分析

假设三条边分别为 a , b , c（a > b），要使得这三条边能组成一个三角形，必须满足： $a + b > c 且 a ? b < c$
所以求能形成三角形的最大周长，可以先将数组排序，再从最大数开始遍历，只要满足 $n u m s [i ? 1] + n u m s [i ? 2] > n u m s [i]$ 的第一个周长就是最大周长（排序后（两边之差小于第三边）必定满足）

3.代码

class Solution {
    public int largestPerimeter(int[] nums) {
        Arrays.sort(nums);
        int i;
        for (i = nums.length - 1;i >= 2;i--){
            if (nums[i - 1] + nums[i - 2] > nums[i]){
                return nums[i - 1] + nums[i - 2] + nums[i];
            }
        }
        return 0;
    }
}

在这里插入图片描述

三、561. 数组拆分 I

1.题目

561. 数组拆分 I

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), …, (an, bn) ，使得从 1 到 n 的 min(ai, bi) 总和最大。
返回该最大总和。

2.分析

举个例子：
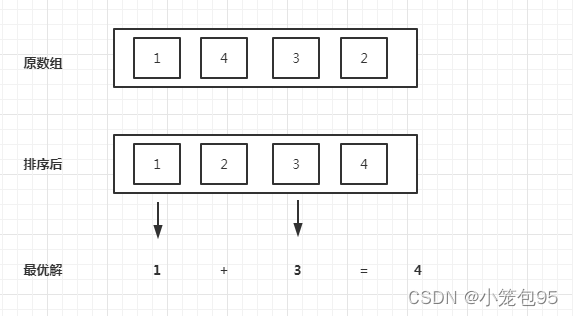
从例子可以发现，要想数对的较小值的总和尽可能大，就要在 $m i n (a, b)$ 时，尽可能将数组中较大的值保留下来。
- 如果最大值和最小值比较，则保留下来的一定是最小值。
- 如果最大值和第二大的值比较，则可以保留下来第二大的值。
所以，只需要将排序后的数组，每两个元素为一对，取较小值的总和，得到的总和就是最大总和。
- 即：遍历排序后的数组，累加偶数位下标对应的值。

3.代码

class Solution {
    public int arrayPairSum(int[] nums) {
        Arrays.sort(nums);
        int i,ans = 0;
        for (i = 0;i < nums.length;i += 2){
            ans += nums[i];
        }
        return ans;
    }
}

在这里插入图片描述

四、881. 救生艇

1.题目

881. 救生艇

第 i 个人的体重为 people[i]，每艘船可以承载的最大重量为 limit。
每艘船最多可同时载两人，但条件是这些人的重量之和最多为 limit。
返回载到每一个人所需的最小船数。(保证每个人都能被船载)。

2.分析

排序后，双指针遍历
对数组 $i n t [] p e o p l e$ 进行排序，再进行遍历。
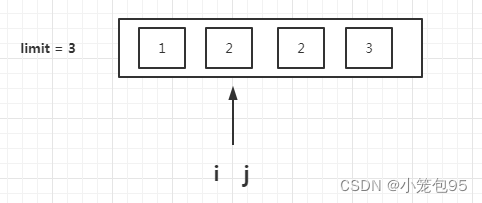
分别用 $i$ 和 $j$ 标记数组两边的元素，如果符合 $p e o p l e [j] + p e o p l e [i] < = l i m i t$ ，说明可以2人一艘船。否则，只能体重较重的人一艘船。
注意遍历的边界：
- 如下图的情况，当 $i = j$ 时，说明最后剩下一个人没上船，所以要将计数 $c o u n t$ 加1

3.代码

class Solution {
    public int numRescueBoats(int[] people, int limit) {
        Arrays.sort(people);
        int i = 0,j = people.length - 1,count = 0;
        while (i < j){
            //小于等于limit，则i++，j--（2人一艘船）
            //大于limit，则j--（一人一艘船）
            if (people[j] + people[i] <= limit){
                i++;
            }
            j--;
            count++;
        }
        return i == j ? ++count : count;
    }
}

在这里插入图片描述

五、324. 摆动排序 II

1.题目

324. 摆动排序 II

给你一个整数数组 nums，将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。
你可以假设所有输入数组都可以得到满足题目要求的结果。

2.分析

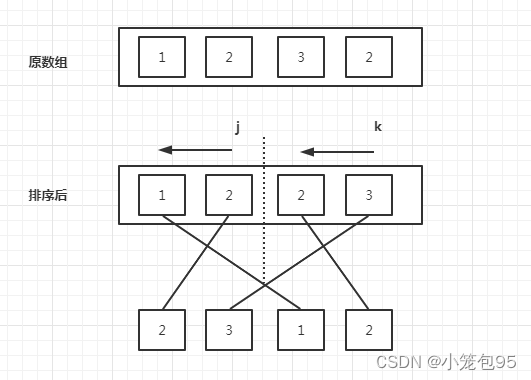
将原数组克隆出一个新数组， $n u m s . c l o n e ();$ ，并对新数组进行排序。
将新数组看成两部分，一部分从下标 $j = (l e n g t h ? 1) > > 1$ 位置开始，另一部分从下标 $k = l e n g t h ? 1$ 开始。
最后，遍历原数组，逆序插入值。当下标为偶数，将新数组下标 $j$ 对应的值存到原数组中， $j$ 自减；当下标为奇数，将新数组下标 $k$ 对应的值存到原数组中， $k$ 自减。

在这里插入图片描述

3.代码

class Solution {
    public void wiggleSort(int[] nums) {
        int i,length = nums.length;
        int[] nums_copy = nums.clone();
        Arrays.sort(nums_copy);
        int j = (length - 1) >> 1,k = length - 1;
        //将数组分成两部分，逆序插入
        for (i = 0;i < length;i++){
            if ((i & 1) == 0){
                nums[i] = nums_copy[j--];
            } else {
                nums[i] = nums_copy[k--];
            }
        }
    }
}

在这里插入图片描述

六、455. 分发饼干

1.题目

455. 分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

2.分析

将胃口数组 $i n t [] g$ 以及饼干数组 $i n t [] s$ 进行排序
优先将饼干满足胃口小的，这样得到满足的数量就是最多的。

3.代码

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int kid = 0,cookie = 0;
        //先满足胃口小的，再满足胃口大的
        while (kid < g.length && cookie < s.length){
            if (g[kid] <= s[cookie]){
                kid++;
            }
            cookie++;
        }
        return kid;
    }
}

在这里插入图片描述

七、1827. 最少操作使数组递增

1.题目

1827. 最少操作使数组递增

给你一个整数数组 nums （下标从 0 开始）。每一次操作中，你可以选择数组中一个元素，并将它增加 1 。
比方说，如果 nums = [1,2,3] ，你可以选择增加 nums[1] 得到 nums = [1,3,3] 。
请你返回使 nums 严格递增的最少操作次数。
我们称数组 nums 是严格递增的，当它满足对于所有的 0 <= i < nums.length - 1 都有 nums[i] < nums[i+1] 。一个长度为 1 的数组是严格递增的一种特殊情况。

2.分析

因为这里不打算修改数组中的元素，所以定义了一个变量 $m a x$ 来存储上一个元素的值（有可能是存储上一个元素修改过的值）
遍历数组，如果当前元素比 $m a x$ 大时，说明还保持着严格递增，直接 $c o n t i n u e$ 进入下一轮循环。
如果当前元素 $< = m a x$ ，则计算当前元素自增到等于 $m a x + 1$ ，需要自增多少次，累加到变量 $c o u n t$ ，循环结束后返回。

3.代码

class Solution {
    public int minOperations(int[] nums) {
        int i,count = 0;
        //较大值
        int max = nums[0];
        for (i = 1;i < nums.length;i++){
            if (nums[i] > max){
                max = nums[i];
                continue;
            }
            max++;
            count += max - nums[i];
        }
        return count;
    }
}

在这里插入图片描述

八、945. 使数组唯一的最小增量

1.题目

945. 使数组唯一的最小增量

给你一个整数数组 nums 。每次 move 操作将会选择任意一个满足 0 <= i < nums.length 的下标 i，并将 nums[i] 递增 1。
返回使 nums 中的每个值都变成唯一的所需要的最少操作次数。

2.分析

数组唯一的最小增量，其实可以解读为：数组排序后，最少操作使数组递增。
所以只要将数组排序后，再以上一题同样的方法来计算操作次数即可。

3.代码

class Solution {
    public int minIncrementForUnique(int[] nums) {
        Arrays.sort(nums);
        int i,count = 0;
        //较大值
        int max = nums[0];
        for (i = 1;i < nums.length;i++){
            if (nums[i] > max){
                max = nums[i];
                continue;
            }
            count += ++max - nums[i];
        }
        return count;
    }
}

在这里插入图片描述

九、611. 有效三角形的个数

1.题目

611. 有效三角形的个数

给定一个包含非负整数的数组，你的任务是统计其中可以组成三角形三条边的三元组个数。

2.分析

对数组进行排序。
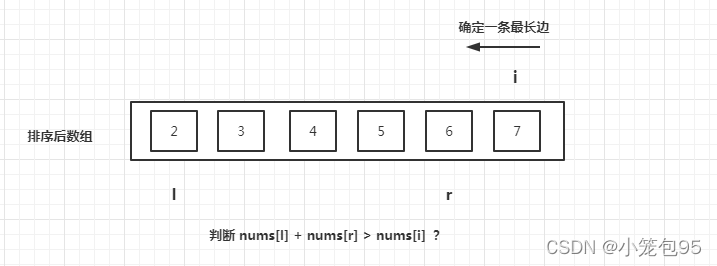
确定一条最长边 $i$ ，再令另外两条边分别从 $l = 0, r = i ? 1$ 开始遍历。
如果判断出现了 $n u m s [l] + n u m s [r] > n u m s [i]$ ，那么 $l$ 和 $r$
之间的元素也必定满足这个条件，不用再遍历这些元素，可以直接累加： $c o u n t + = r ? l;$ ，累加后 $r$ 左移一位。否则， $l$ 右移一位。

3.代码

class Solution {
    public int triangleNumber(int[] nums) {
        Arrays.sort(nums);
        int i,count = 0;
        for (i = nums.length - 1;i >= 2;i--){
            int l = 0,r = i - 1;
            while (l < r){
                if (nums[l] + nums[r] > nums[i]){
                    count += r - l;
                    r--;
                } else {
                    l++;
                }

            }
        }
        return count;
    }
}