代码以前都敲过(抄过)就不复现了,主要记录一下理论学习中的疑惑点和重点
多项式回归
本块代码应该是通过高次多项式想去拟合曲线,但是不确定多高次比较合适,所以设了三个值,然后结果发现4次最贴近。
以最高次4次为例,求解时用每个样本点x的四次方代替了原本的一次方x,也就是如果我原来的数据集x取值1,2,3,现在我用1,16,81作为x,我只是变动了x的值,却还可以用线性回归的方式去求解。
cross-validation与把数据集分成train和test两part的区别
cross-validation把数据集分十份,每一份都会做一次test,剩下的九份就是train,算出了十个模型,再求均值。比单纯一次分train和test更能避免极值数据对模型的影响,但是计算成本肉眼可见的急剧增加,但是回归可以用mapreduce去做吧?
逻辑回归(需要继续学习)
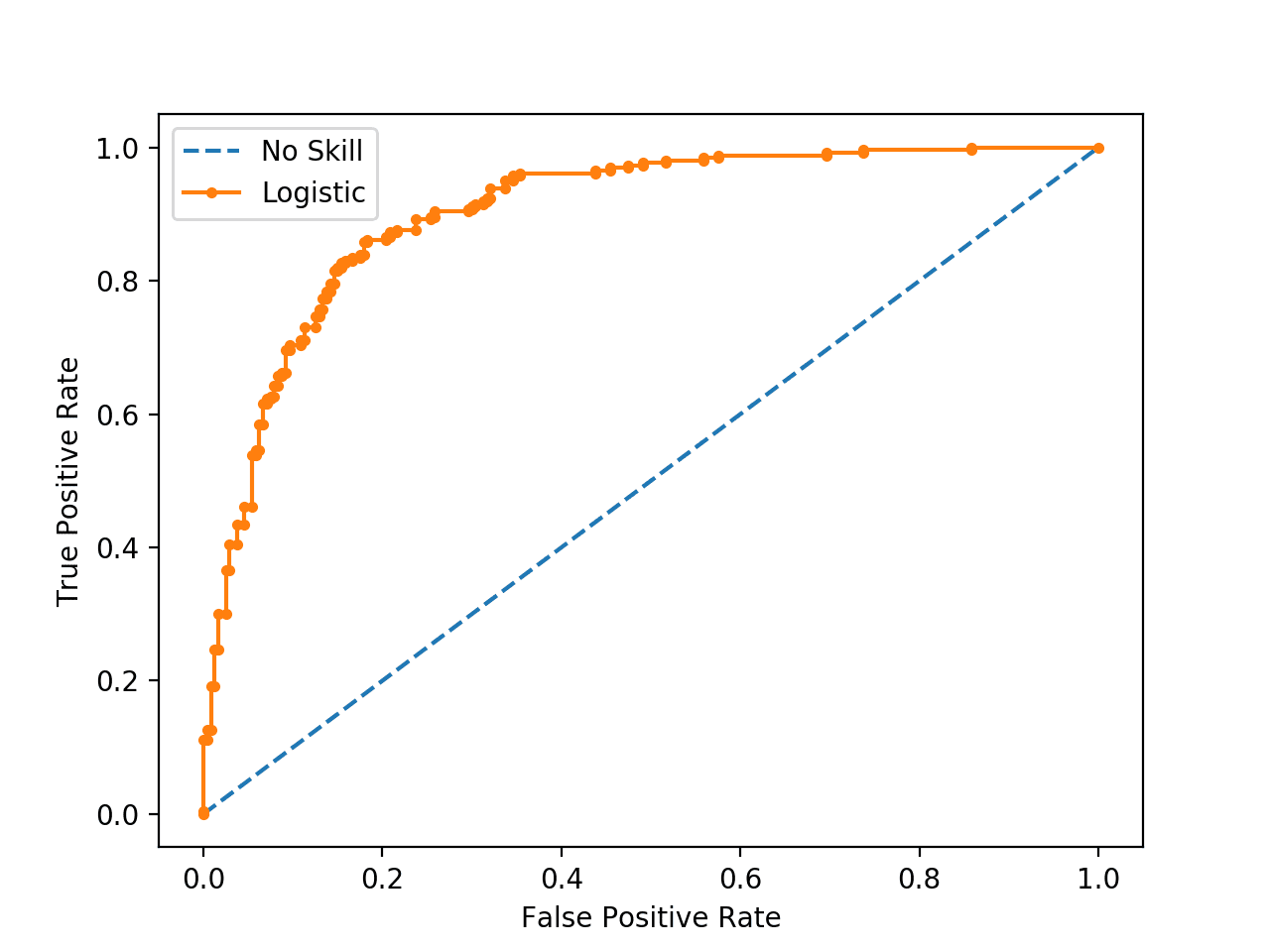
ROC曲线与AUC指标
TPR与FPR
TPR = TP / (TP + FN)
真实结果positive样本里面的真阳率(eg在一众真实孕妇中,检测出怀孕的比率)
FPR = FP / (FP + FN)
真实结果negtive样本里面的假阳率(eg在一众没怀孕的女性中,检测出人家怀孕的比率)
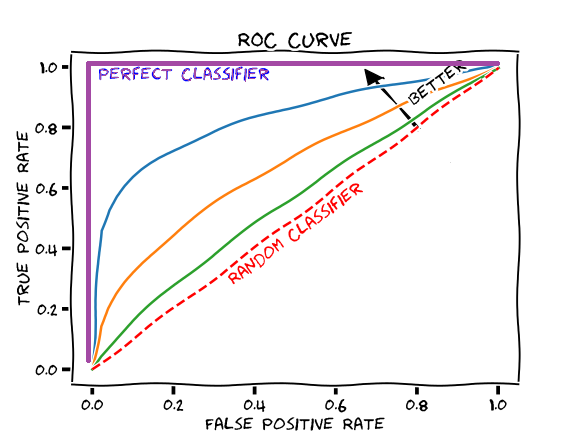
ROC曲线
ROC曲线的横轴就是FPRate(假阳率),纵轴就是TPRate(真阳率),当二者相等时,表示的意义则是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的,此时AUC为0.5
现实案例中,两者之间会有侧重,没测出新冠可能要比错误地测出新冠的代价要大,所以可以人为的把我的模型cut-off value设置的比0.5要小,从而把更多的点归到1里,宁肯错杀十个不肯放过一个
AUC指标
AUC的概率意义是随机取一对正负样本,正样本得分大于负样本的概率
AUC的最小值为0.5,最大值为1,取值越高越好
AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
最终AUC的范围在[0.5, 1]之间,并且越接近1越好
?
?