[数据结构与算法]【LeetCode】每日一题2021/12/16

• 思路
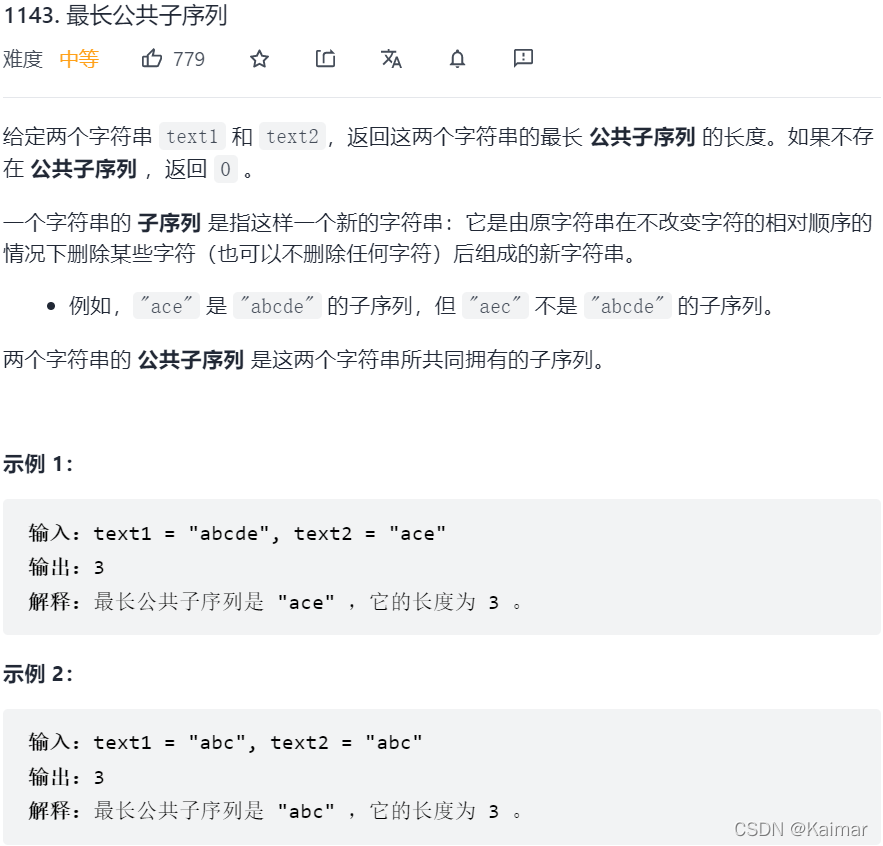
  这道题的难点在于这个子序列的元素是不一定挨着的。但是和上一道最长重复子序列的题目又非常像。
  难点还是在于怎么确定前后元素的位置关系，体现在状态转移方程中是怎么体现的？
  dp数组的定义和下标含义：dp[s1.length][s2.length]，dp[i][j]代表截止字符串1的位置i和字符串2的位置j，两者的最长公共子序列长度；
  dp的状态转移方程：当s1[i]==s2[j]时，dp[i][j] = dp[i-1][j-1]+1，不相等时就等于上一个值dp[i][j]=dp[i-1][j-1]，这样才能将之前的值记录下来，否则无法定位到上一个相等元素的位置；
  dp的初始化：全部初始化为0；
  遍历顺序：外s1，内s2，从前向后依次遍历；
  举例验证发现有问题，参考题解
  
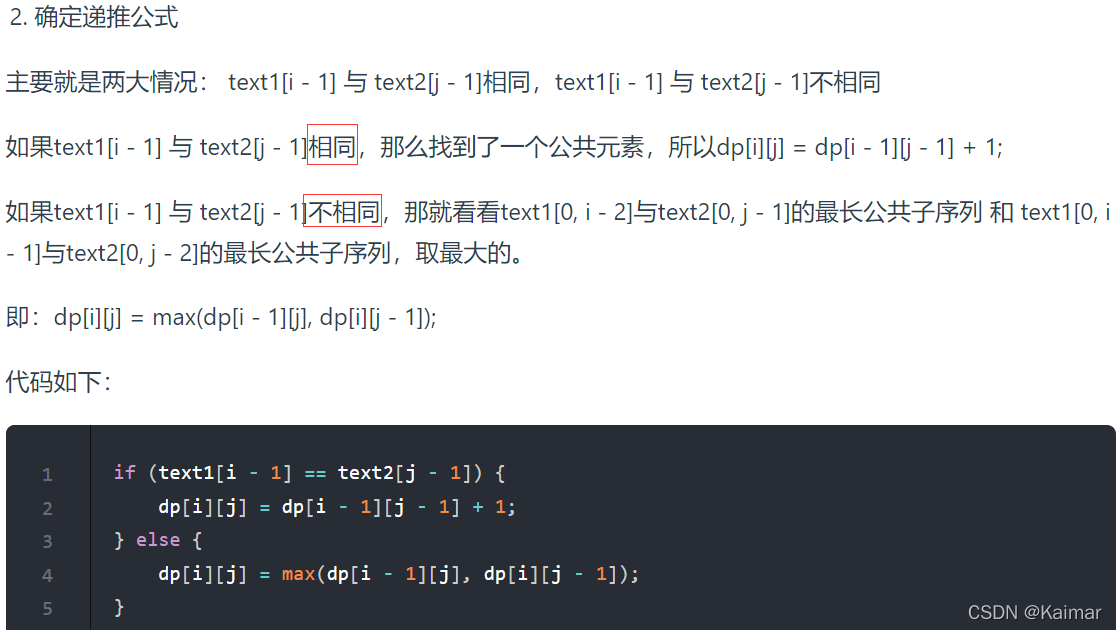
  还有一点要注意，因为我们要去找与前面元素的关系，所以实际上遍历是从下标1开始的。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length(), len2 = text2.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        // 已经默认初始化了，dp[0][j]、dp[i][0]全为0
        for (int i = 1; i < len1 + 1; i++) {
            for (int j = 1; j < len2 + 1; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[len1][len2];
    }
}