题目描述：

解题思路:

思想

就一句话：每次在上次能跳到的范围（end）内选择一个能跳的最远的位置（也就是能跳到max_far位置的点）作为下次的起跳点！

详解：

规的思维就是暴力穷举，把所有可行的跳跃方案都穷举出来，计算步数最少的。穷举的过程会有重叠子问题，用备忘录消除一下，就成了自顶向下的动态规划。

不过直观地想一想，似乎不需要穷举所有方案，只需要判断哪一个选择最具有「潜力」即可，这就是贪心思想来做，比动态规划效率更高。

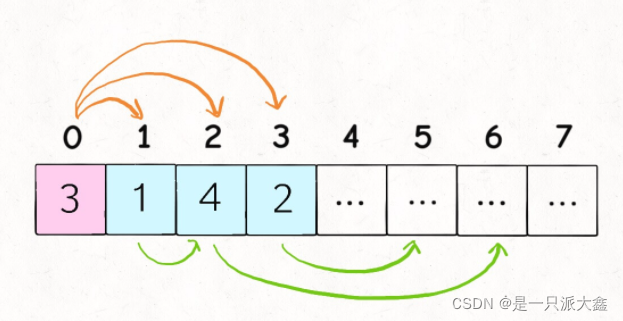
?比如上图这种情况，我们站在索引 0 的位置，可以向前跳 1，2 或 3 步，你说应该选择跳多少呢？

显然应该跳 2 步调到索引 2，因为?nums[2]?的可跳跃区域涵盖了索引区间?[3..6]，比其他的都大。

这就是思路，我们用?i?和?end?标记了可以选择的跳跃步数，farthest?标记了所有选择?[i..end]?中能够跳到的最远距离，jumps?记录跳跃次数。

看不懂？再来详解：

?

?

解题代码：

int jump(int* nums, int numsSize){
    if(numsSize == 1) return 0;
    int end = 0 , farthest = 0;
    int jumps = 0;
    for(int i = 0; i < numsSize - 1; i++){
        farthest = fmax(nums[i] + i , farthest); //记录当前能到达的最远距离
        if(end == i){
            jumps++;
            end = farthest; //模拟每次能跳到的最远距离，然后“跳到”最远距离上，这时步数+1
            //当end == i 时表示，上一次跳jumps次已经到最大距离了，之后的距离肯定得+1
        }
    }
    return jumps;
}