[数据结构与算法]leetcode 787. Cheapest Flights Within K Stops | 787. K 站中转内最便宜的航班（BFS）

题目

https://leetcode.com/problems/cheapest-flights-within-k-stops/

题解

这题挺坑的实际上。DFS 超时了，因为涉及到步数限制 k，所以并不能加缓存，然后去看了答案。
答案给了一种 BFS 解法，看完思路我就开始一顿写。

一开始是按照如果走回头路的开销比不走回头路更小的话，就走回头路这种思路来写的。提交的时候发现，能不能走回头路，这个问题会比较复杂。
回头路是可以走的，但是不能简单的用回头路的开销去覆盖原有的开销，因为在你走回头路的时候，3步到①可能比2步到①的实际开销更小，但你不能确定在之后剩余的步数中，哪种选择更好。

说白了就是，当你还不能确定要不要走重复路线的时候，一维的dist不能同时保存走或不走两种结果。
所以后来用了 int[2] 存储[i，从src到i的距离。详见注释吧。

最后，贴一下混乱的草稿。

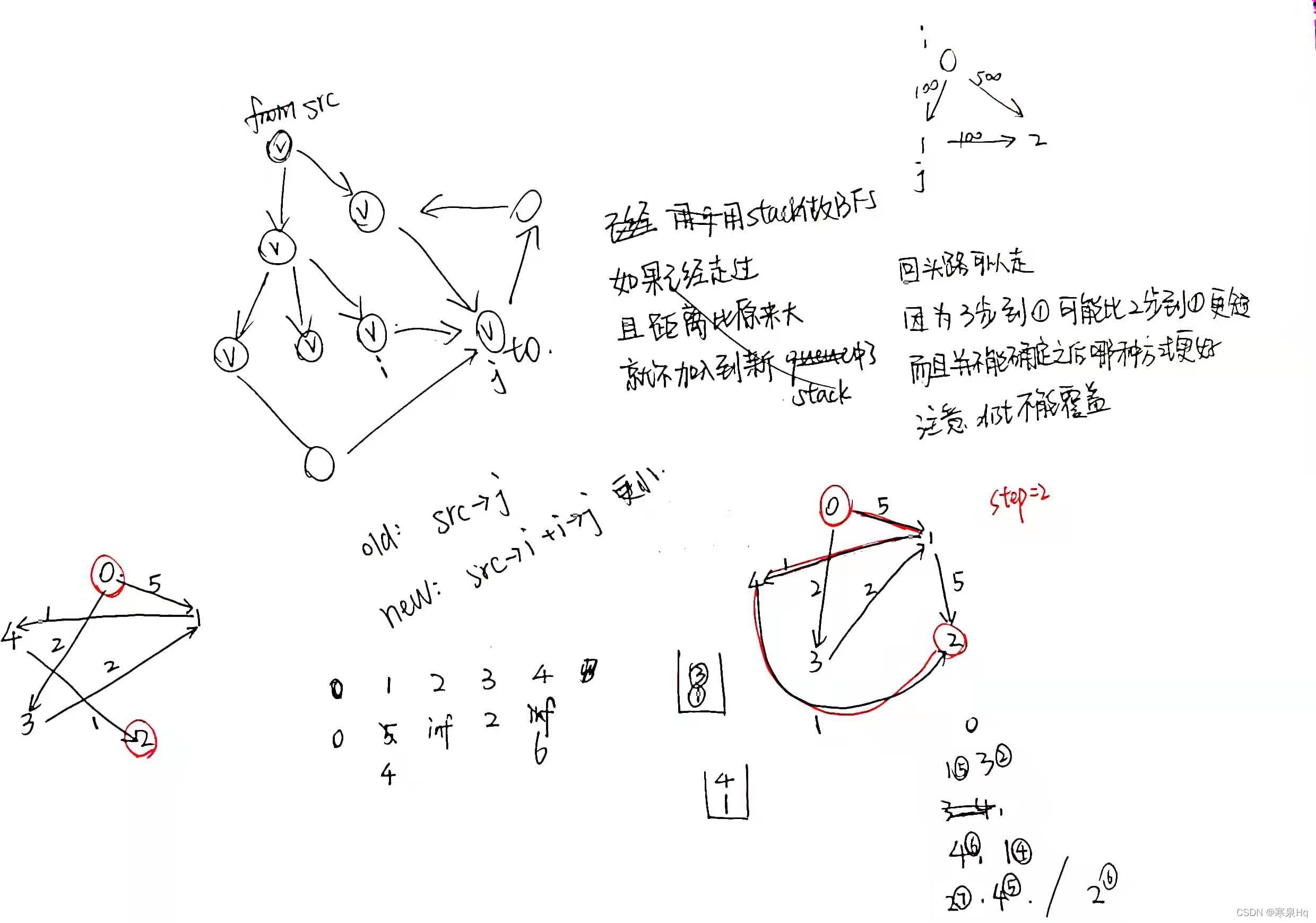
class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int[][] graph = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(graph[i], -1);
        }
        for (int[] f : flights) {
            graph[f[0]][f[1]] = f[2];
        }
        // BFS
        int[] dist = new int[n]; // dist[i]表示src->i的距离
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[src] = 0;

        // 此处使用int[]的原因是，不能简单的从dist中拿最小结果，因为在你走回头路的时候，3步到①可能比2步到①的实际开销更小，
        // 但你不能确定在之后剩余的步数中，哪种选择更好。
        // 说白了就是，当你还不能确定要不要走重复路线的时候，一维的dist不能同时保存走或不走两种结果。
        Stack<int[]> stack = new Stack<>(); // [i，从src到i的距离]。
        stack.push(new int[]{src, 0});

        int step = 0;
        while (step++ <= k) {
            if (stack.isEmpty()) break;
            Stack<int[]> newStack = new Stack<>();
            while (!stack.isEmpty()) {
                int[] pair = stack.pop(); // pair = [i，从src到i的距离]
                int i = pair[0];
                for (int j = 0; j < n; j++) { // src->i->j
                    // 如果之前已经走过，只有当距离比原来小的时候才加入计算
                    // 如果之前没走过，则当前距离肯定比INF小，所以肯定会加入计算
                    if (i != j && graph[i][j] >= 0 && pair[1] + graph[i][j] < dist[j]) { 
                        dist[j] = pair[1] + graph[i][j];
                        newStack.add(new int[]{j, dist[j]});
                    }
                }
            }
            stack = newStack;
        }
        return dist[dst] == Integer.MAX_VALUE ? -1 : dist[dst];
    }
}