字典序
1 < 2
10 < 9,因为 10 的前缀是 1,比 9 小
112 < 12,因为 112 的前缀是 11,比 12 小
十大排序
排序稳定性 相同权重的值,排序后是否还能保证先后顺序一致
如:现有序列 {4, 2, 3, 2, 1}
标记为 {4, 第一个2, 3, 第二个2, 1}
不稳定排序后可能变为 {1, 第二个2, 第一个2, 3, 4}
而稳定排序则变为 {1, 第一个2, 第二个2, 3, 4}
| 比较排序 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| ? 快速排序 | n log ? 2 n n\log_{2}{n} nlog2?n | n log ? 2 n n\log_{2}{n} nlog2?n | n 2 n^2 n2 | log ? 2 n \log_2n log2?n | × \times × |
| ?堆排序 | n log ? 2 n n\log_{2}{n} nlog2?n | n log ? 2 n n\log_{2}{n} nlog2?n | n log ? 2 n n\log_{2}{n} nlog2?n | 1 1 1 | × \times × |
| 选择排序 | n 2 n^2 n2 | n 2 n^2 n2 | n 2 n^2 n2 | 1 1 1 | × \times × |
| 希尔排序 | n log ? 2 n n\log_2n nlog2?n | n 1.3 n^{1.3} n1.3 | n 2 n^2 n2 | 1 1 1 | × \times × |
| 稳定排序 | |||||
| 冒泡排序 | n n n | n 2 n^2 n2 | n 2 n^2 n2 | 1 1 1 | √ √ √ |
| 插入排序 | n n n | n 2 n^2 n2 | n 2 n^2 n2 | 1 1 1 | √ √ √ |
| ?归并排序 | n log ? 2 n n\log_{2}{n} nlog2?n | n log ? 2 n n\log_{2}{n} nlog2?n | n log ? 2 n n\log_{2}{n} nlog2?n | n n n | √ √ √ |
| 非比较排序 | |||||
| 计数排序 | n + k n+k n+k | n + k n+k n+k | n + k n+k n+k | k k k | √ √ √ |
| 桶排序 | n + k n+k n+k | n + k n+k n+k | n 2 n^2 n2 | n n n | √ √ √ |
| 基数排序 | n k nk nk | n k nk nk | n k nk nk | n + k n+k n+k | √ √ √ |
不稳定排序
快速排序 - 每次排序让标志位一边都比它大,另一边都比它小

void quickSort(int l, int r)
{
if (l > r) return;
int i = l;
int j = r;
int index = a[i];
while (i < j) // break: i == j
{
while (i < j && a[j] >= index) --j; // break: a[j] < index
if (i < j) a[i++] = a[j]; // 把小于index的放左边
while (i < j && a[i] < index) ++i; // break: a[i] >= index
if (i < j) a[j--] = a[i]; // 把大于index的放右边
}
// a[i]左边都是比index小的,右边都是比index大的
// 把index的值还给a[i]
a[i] = index;
quickSort(l, i - 1); // 递归搜索左半部分
quickSort(i + 1, r); // 递归搜索右半部分
}
缺点:数据已经有序时,时间复杂度退化为 O ( n 2 ) O(n^2) O(n2)
优化方案
- 排序前判断检测区间是否有序
- 但这种方案对于随机数组毫无意义,只适用于经常出现有序片段场景
- 三数取中 基准值使用
i和j的中间值
- 如果在每个递归中都将区间划分为均等的两份,那么时间复杂度将是最优的 O ( n log ? n ) O(n\log{n}) O(nlogn)
- 如果在每个递归中都将区间划分为
1和n-1两份,快排就退化为递归版的冒泡排序 - 而一般情况我们都以
i或j作为基准值,就容易发生区间划分不均的情况
-
多线程优化 每个区间使用单独线程排序(需要注意递归深度)
-
插入排序优化 区间较小时,使用插入排序
堆排序 -
优点:时间复杂度恒定为 O ( n log ? n ) O(n \log{n}) O(nlogn)

class minHeap
{
private:
int *a;
int capacity;
int size;
public:
minHeap (int _capacity): size(0), capacity(_capacity) { a = new int[capacity]; }
inline int parent (int i) { return (i - 1) / 2; }
inline int leftChild (int i) { return 2 * i + 1; }
inline int rightChild (int i) { return 2 * i + 2; }
// 从树底插入节点
void push (int val)
{
if (size == capacity) return;
int i = size++;
a[i] = val;
// siftUp
while (i > 0 && a[i] < a[parent(i)]) // i 比父节点小
{
swap(a[i], a[parent(i)]);
i = parent(i);
}
}
// 弹出树根
int pop ()
{
if (!size) return -1;
if (size == 1) return a[--size];
int root = a[0];
// 以树底作为新的树根
a[0] = a[--size];
siftDown(0);
return root;
}
void siftDown (int i)
{
if (i >= size) return;
int l = leftChild(i), r = rightChild(i);
int s = i; // 标记最小的节点为 s
if (l < size && a[l] < a[s]) s = l;
if (r < size && a[r] < a[s]) s = r;
if (s != i)
{
swap(a[i], a[s]);
siftDown(s);
}
}
};
选择排序 - 每次遍历选出最小的和 first++ 交换
如 5 8 5 1 9,第一遍排序后两个 5 的相对顺序就被破坏了,因此不稳定

void selectionSort(int *a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int minIndex = i;
for (int j = i + 1; j < n; j++)
{
if (a[j] < a[minIndex]) minIndex = j;
}
swap(a[i], a[minIndex]);
}
}
希尔排序 - 分为多个子序列进行插入排序
87 6 543 2 1
476 5 832 1
4 365 8 721
4 3 258 7 61
4321 8 7 6 5
23418 7 6 5
2 14387 6 5
2 1 43876 5
2 1 4 38765
2 1 4 3 6785
214 3 6 5 8 7
1243 6 5 8 7
1 2436 5 8 7
1 2 3 4658 7
1 2 3 4 5687
1 2 3 4 5 687
1 2 3 4 5 6 7 8
void shellSort(int *a, int n)
{
for (int half = n / 2; half > 0; half /= 2)
{
// 将插入排序中的 1 改为half
for (int i = half; i < n; i++)
{
int j = i - half;
int current = a[i];
while (j >= 0 && a[j] > current)
{
a[j + half] = a[j];
j -= half;
}
a[j + half] = current;
}
}
}
稳定排序
冒泡排序 - 每次选两个向后依次比较

void bubbleSort(int *a, int n)
{
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - 1 - i; j++)
{
if (a[j] > a[j + 1]) swap(a[j], a[j + 1]);
}
}
}
直接插入排序(打牌) - 每次选一个依次和前面比
优点:数据几乎有序时时间复杂度达到 O ( n ) O(n) O(n)

void insertSort(int *a, int n)
{
for (int i = 1; i < n; i++)
{
int j = i - 1;
// 要插入的数标记为红色
int current = a[i];
while (j >= 0 && a[j] > current)
{
// 绿色的数依次往后移动
a[j + 1] = a[j];
--j;
}
// 红色的数插入到正确的位置
a[j + 1] = current;
}
}
归并排序

function mergeSort(arr) {
var len = arr.length;
if (len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
var result = [];
while (left.length>0 && right.length>0) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
非比较排序
计数排序 - 数组记录个数

桶排序 - 分桶依次排序
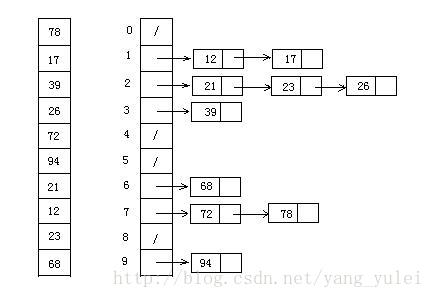
假设元素个数为 n n n ,均匀分布在 m m m 个桶中,每个桶中元素个数 k = n m k = \frac{n}{m} k=mn?
对每个桶进行快速排序最快耗时 k log ? k k\log k klogk 即 n m log ? n m \frac{n}{m}\log\frac{n}{m} mn?logmn?, m m m 个桶即 n log ? n m n\log\frac{n}{m} nlogmn?
最好情况:当 n n n 和 m m m 非常接近时,时间复杂度为 n n n
最坏情况:数据有序导致快排耗时 k 2 k^2 k2 即 n 2 m 2 \frac{n^2}{m^2} m2n2?,且分布在 1 1 1 个桶中,时间复杂度 n 2 n^2 n2
基数排序

排序问题
三色旗(荷兰国旗)问题
// 若遍历到0,它属于前部,因此交换a[cur]和a[beg],然后cur和beg加一(beg表示beg前的已经都排好了),注意2一定不会在0前面,因为遍历到2时会将2放到尾部
// 若遍历到1,它属于中部,但我们只要将0放到前部,2放到尾部即可,因此只需cur加一
// 若遍历到2,它属于后部,因此交换a[cur]和a[end],但cur可能是0和1,如果cur前进会导致0无法放在前部,因此cur不变end减一
void sort(int *a)
{
int cur = 0;
int l = 0, r = n - 1;
while (cur <= r)
{
if (a[cur] == 0)
{
swap(a[cur++], a[l++]);
}
else if (a[cur] == 1)
{
++cur;
}
else
{
swap(a[cur], a[r]);
--r;
}
}
}
【注】:排序动图源自 十大经典排序算法(动图演示)