[数据结构与算法]数据结构查找-7-8 中序遍历树并判断是否为二叉搜索树

7-8 中序遍历树并判断是否为二叉搜索树 (20 分)

对给定的有N个节点（N>=0）的二叉树，给出中序遍历序列，并判断是否为二叉搜索树。

题目保证二叉树不超过200个节点，节点数值在整型int范围内且各不相同。

输入格式:

第一行是一个非负整数N，表示有N个节点

第二行是一个整数k，是树根的元素值

接下来有N-1行，每行是一个新节点，格式为?r d e?三个整数，

r表示该节点的父节点元素值（保证父节点存在）；d是方向，0表示该节点为父节点的左儿子，1表示右儿子；e是该节点的元素值

输出格式:

首先输出二叉树的中序遍历序列，每个元素占一行。对于空树，不输出任何内容。

然后如果给定的树是二叉搜索树，输出Yes?否则输出No

输入样例:

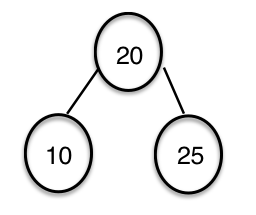
对于图片中的二叉树：

3
20
20 0 10
20 1 25

结尾无空行

输出样例:

10
20
25
Yes

结尾无空行

#include<bits/stdc++.h>
#define N 500005
#define inf 0x3f3f3f3f
using namespace std;
map<int,int>lc,rc;
int n,s;
void zhong(int s)
{
        if(lc.count(s)==1)
                zhong(lc[s]);
        cout<<s<<endl;
        if(rc.count(s)==1)
                zhong(rc[s]);
}
int main()
{
        cin>>n;
        if(n==0)
        {
                cout<<"Yes"<<endl;
                return 0;
        }
        cin>>s;
        int flag=0;
        for(int i=0;i<n-1;i++)
        {
                int r,d,e;
                cin>>r>>d>>e;
                if(d==0)
                {
                        if(e>r) flag=1;
                        lc[r]=e;
                }
                else
                {
                        if(e<r) flag=1;
                        rc[r]=e;
                }
        }
        zhong(s);
        if(flag==1)
                cout<<"No"<<endl;
        else
                cout<<"Yes"<<endl;
}