1.假设二叉树采用二叉链存储结构存储,设计一个算法计算一棵给定二叉树的所有叶子节点个数。
int LeafNodes(BTNode *b)
{
int num1,num2;
if (b == NULL)
return 0;
else if(b->1child==NULL && b->rchild==NULL)
return 1;
else
{
num1=LeafNodes(b->1child);
num2=LeafNodes(b->rchild);
return(num1+num2);
}
}
2.假设二叉树采用二叉链存储结构存储,设计一个算法计算一棵给定二叉树的所有双分支节点 。
int DSonNodes(BTNode *b)
{
int num1,num2,n;
if (b==NULL)
return 0;
else if (b->1child==NULL || b->rchild==NULL)
n=0; //为单分支或叶子节点时,不计
else
n=1; //为双分支节点时,计 1
num1=DSonNodes(b->1child); //递归求左子树的双分支节点数
num2=DSonNodes(b->rchild); //递归求右子树的双分支节点数
return (num1+num2+n);
}
3.假设二叉树采用二叉链存储结构存储,设计一个算法求其中最小值的节点值。
void FindMinNode(BTNode *b,ElemType &min)
{
if(b->data < min)
min = b->data;
FindMinNode(b->lchild,min); // 在左子树中寻找最小节点值
FindMinNode(b->rchild,min); // 在右子树中寻找最小节点值
}
void MinNode(BTNode *b)
{
if(b!=NULL)
{
ElemType min = b->data;
FindMinNode(b,min);
printf("Min = %d\n",min);
}
}
4.假设二叉树采用二叉链存储结构存储,所有节点的值为正整数,设计一个算法求所有节点值之和。
int FindSum(BTNode *b)
{
if(b==NULL)
return 0;
else
return (b->data + FindSum(b->lchild)+FindSum(b->rchild));
}
5.假设二叉树采用二叉链存储结构存储,为设计一个算法求其中节点值为 x的节点个数。
int FindCount(BTNode *b,ElemType x)
{
if(b==NULL)
return 0;
else if(b->data == x)
return (1+FindCount(b->lchild,x) + FindCount(b->rchild,x));
else
return (FindCount(b->lchild,x) + FindCount(b->rchild,x));
}
6.假设二叉树采用二叉链表存储结构,设计一个递归算法求二叉树的高度。
int BTNodeDepth (BTNode *b)
{
int lchilddep, rchilddep;
if (b==NULL)
return(0); //空树的高度为 0
else
{
childdep=BTNodeDepth(b->lchild); //求左子树的高度为 lchilddep
rchilddep-BTNodeDepth(b->rchild); //求右子树的高度为 rchilddep
return (lchilddep > rchilddep) ? (lchilddep+1) : (rchilddep+1);
}
}
7.假设二叉树 b 采用二叉链存储结构,设计一个算法 void findparent(BTNode*b,ElemType x,BTNode *&p)求指定值为 x 的节点的双亲节点 p。
提示:根节点的双亲为 NULL,若在 b 中未找到值为 x 的节点,p 亦为 NULL,并假设二叉树中所有节点值是唯一的。
算法思想:设在二叉树 b 中查找 x 节点的双亲 p 的过程为 f(b,x,p),找到后 p 指向 x 节点的双亲节点,否则 p=NULL。当 b 为空树或根节点值为 x 时,p=NULL,否则在左子树中查找,若未找到则在右子树中查找。
void findparent (BTNode *b,ElemType x, BTNode *&p)
{
if (b!=NULL)
{
if(b->data==X)
p=NULL;
else if (b->lchild != NULL && b->lchild->data == x)
p=b;
else if (b->rchild != NULL && b->rchild->data == x)
p=b;
else
{
findparent (b->lchild, x,p);
if (p==NULL)
findparent (b->rchild, x,p);
}
}
else p=NULL;
}
8.二叉树 T 采用二叉链表存储结构,用根结点用 t 指示, 设计一个算法,求指针 p 所指结点的双亲结点。
BTNode* getParent(BTNode *t, BTNode *p)
{ //只考虑 p 是正确的输入情况下
if(t == NULL) //当树为空时
return NULL; //没有双亲结点
if(t == p) //当 p 所指结点为根结点时候
return NULL; //没有双亲结点
if(t->lchild == p || t->rchild == p) //当 t 的左孩子或者右孩子为 p 时
return t; //t 是 p 的双亲结点
BTNode *parent = getParent(t->lchild,p); //向左子树一直递归遍历,寻找符合条件的双亲结点
if(parent != NULL) //若找到
return parent; //返回其双亲结点
else
return getParent(t->rchild,p); //否则,向右子树递归遍历
}
9.假设二叉树采用二叉链存储结构,设计一个算法输出值为 x的结点的所有祖先。
bool ancestor(BTNode *b, ElemType x)
{
if(b == NULL) //若 b = NULL
return false; //f(b,x) = false
else if(b->lchild!= NULL && b->lchild->data == x || b->rchild!= NULL && b->rchild->data == x)
{
//若结点 b 的左孩子或右孩子的 data 域为 x
printf("%c",b->data); //f(b,x) = true,并输出 b->data
return true;
}
else if(ancestor(b->lchild, x) || ancestor(b->rchild, x))
{
//若 f(b->lchild,x) 为 true 或 f(b->rchild,x) 为 true
printf("%c",b->data); // f(b,x) = true,并输出 b->data
return true;
}
else // 其他情况
return false; //f(b,x) = false
}
10.设计一个算法把树 b 的左、右子树进行交换。要求算法的空间复杂度为 O(1)。
//本算法的时间复杂度为 O(n),空间复杂度为 O(1)。
void Swap (BTNode * &b)
{
BTNode *temp;
if(b!=NULL)
{
Swap2 (b->1chi1d); //交换左子树
Swap2 (b->rchild); //交换右子树
temp-b->lchild; //将*b 节点的左、右指针域进行交换
b->lchild=b->rchild;
b->rchild=temp;
}
}
11.假设二叉树采用链式存储结构进行存储,设计一个算法,求二叉树 b 中值为 x 的结点层号
//调用本算法时 h 指出根节点的层次即为 1
int NodeLevel (BTNode *b,ElemType x,int h)
{
int hl;
if(b==NULL) //空树时返回 0
return 0;
else if (b->data==X) //找到节点 x 时
return h;
else
{
hl=NodeLevel (b->lchild, x, h+1); //在左子树中递归查找
if(hl==0)
return NodeLevel (b->rchild, x,h+1); //左子树中未找到时在右子树中查找
else
return hl;
}
}
12.求先序遍历序列中第k(1≤k≤二叉树中节点个数)个节点的值。
算法思想:用一个全局变量 n(初值为 1)保存先序遍历时访问节点的序号。当二叉树 b为空时返回特殊字符‘ ’ (空格字符),当 k==n 时表示找到了满足条件的节点,返回 b->data;当 k≠n 时,在左子树中查找,若找到了返回该值,否则在右子树中查找,并返回其结果。
int n=1; //全局变量
ElemType PreNode(BTNode *b,int k)
{
ElemType ch;
if (b==NULL)
return' ';
if (n=-k)
return(b->data);
n++;
ch=PreNode(b->lchild,k); //遍历左子树
if(ch!=' ')
return(ch); //在左子树中找到后返回
ch=PreNode(b->rchild,k); //遍历右子树
return(ch); //返回右子树中的遍历结果
}
13.求中序遍历序列中第k(1≤k≤二叉树中节点个数)个节点的值。
int n=1; //全局变量
ElemType InNode (BTNode *b, int k)
{
ElemType ch;
if (b==NULL)
return' ’;
ch=InNode(b->lchild,k); //遍历左子树
if (ch!=' ') //在左子树找到了便返回 ch
return ch;
else
{
if (n==k)
return b->data;
n++;
return InNode(b->rchild,k); //返回在右子树中查找的结果
}
}
14.求后序遍历序列中第k(1≤k≤二叉树中节点个数)个节点的值。
int n=1; //全局变量
ElemType PostNode(BTNode *b,int k)
{
ElemType ch;
if (b==NULL)
return ' ';
ch=PostNode(b->1child,k); //遍历左子树
if (ch!=' ') //在左子树找到了便返回 ch
return ch;
else
{
ch=PostNode(b->rchild,k); //遍历右子树
if (ch!=' ') //在右子树找到了便返回 ch
return ch;
if (n==k)
return b->data;
n++;
}
}
15.二叉树的带权路径长度为每个叶结点的深度与权值之积的总和,可以采用先序遍历或层序遍历解决。
算法思想:基于先序递归遍历的算法思想:采用一个 static 变量记录 wpl,把每个结点的深度作为递归函数的一个参数传递。
int wpl_PreOrder(BiTree root, int deep)
{
static int wpl = 0; //定义一个 static 全局变量存储 wpl
if(root->lchild == NULL && root->rchild == NULL)
wpl = wpl + deep*root->weight; //为叶子结点直接累计 wpl
if(root->lchild != NULL)
wpl_PreOrder(root->leight, deep+1);
if(root->rchild != NULL)
wpl_PreOrder(root->rchild, deep+1);
return wpl;
}
16.设计一个算法,将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。
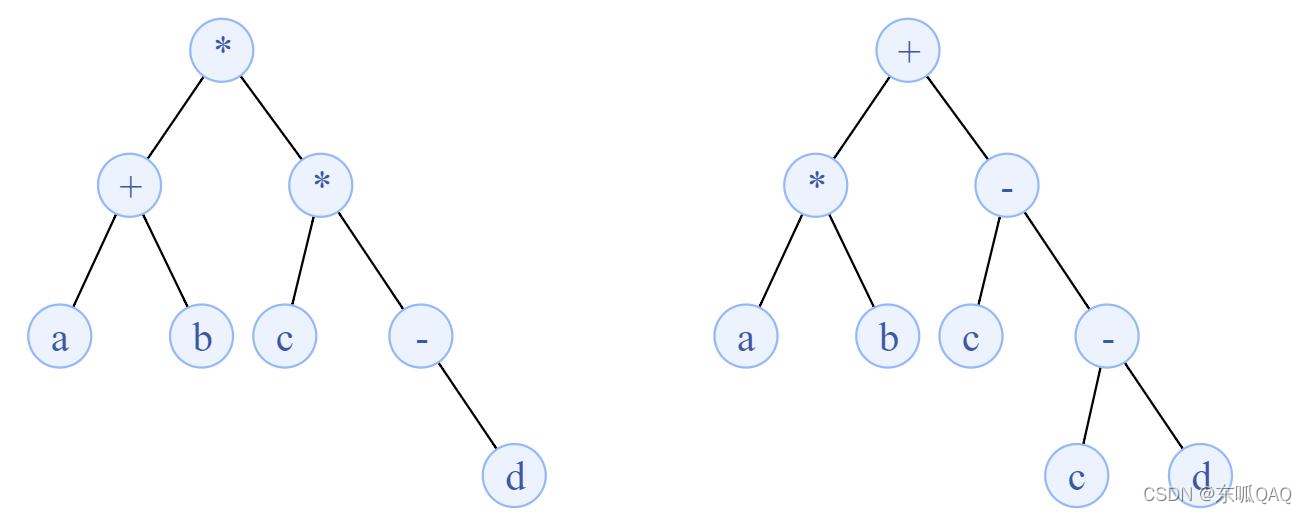
输出等价的中缀表达式分别为 (a+b)(c(-d)) 和 (a*b)+(-(c-d)) 。
算法思想:将二叉树的中序遍历递归算法稍加变形即可得到。除根结点和叶子结点外,遍历到其他结点是在遍历其左子树之前加上左括号,遍历完右子树后加上右括号
typedef struct node
{
char data[10];
struct node *left, *right;
}BTree;
void BtreeToExp(BTree *root, int deep)
{
if(root == NULL)
return ;
else if(root->left == NULL && root->right == NULL) //若为叶子结点
printf("%s", root->data);
else
{
if(deep > 1)
printf("("); //若有子表达式则加 1 层括号
BtreeToExp(root->left, deep+1);
printf("%s", root->data);
BtreeToExp(root->right, deep+1);
if(deep > 1)
printf(")"); //若有子表达式则加 1 层括号
}
}