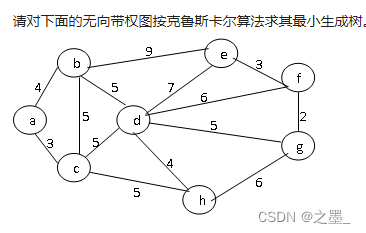
数据结构与算法—Kruskal算法求最小生成树
并查集
并查集 (英文:Disjoint-set data structure,直译为不交集数据结构)
是一种 数据结构 ,用于处理一些 不交集 (Disjoint sets,一系列没有重复元素的集合)的合并及查询问题
在kruskal算法中,我们要用到并查集来判断新加入的边是否和已加入的边属于同一棵树,即是否加入后会构成回路,由于最小生成树不允许有回路,所以在求最小生成树的过程中不能加入会构成回路的边
克鲁斯卡尔算法的关键点在于如何判断添加的一个边是否会与其他的边构成回路,因此这里就需要用到并查集
元素x的上级结构可能构成一颗树 那么要找到这颗树的根结点也就是x的最高级 就需要从x的上级一层层向上查找
find函数 寻找最高上级
int Find(int x)
{///查找最高上级
if(pre(x) != x) //还没找到最高上级
return Find(pre[x]);//继续向上查找
return x;
}
find函数 路径压缩 寻找最高上级
优化的find()函数 采用路径压缩 让所有子结点直接和根结点相连 即树的高度为1
int FindPro(int x)
{///路径压缩 查找函数优化版
if(pre[x] == x)
return x; //当找到最高上级时结束递归
return pre[x] = FindPro(pre[x]); //找到最高上级并设为对应结点的直接上级
}
union函数 合并两无关边
将本无关联的两条边加入同一个集合中 选择任意一条边的最高上级认另一条边的最高上级作为上级 实现两条边成为同一个集合(阵营)
void union(int i,int j)
{///将两个边加入到一个集合中
pre[Find(i)] = Find(j);//将任意一个边的最高上级变成另一条边的下级 这里j的上级作为i的最高上级
}
Kruskal算法求最小生成树
题目一
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数,求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|
由 V 中的全部 n 个顶点和 E 中 n?1 条边构成的无向连通子图被称为 G 的一棵生成树其中边的权值之和最小的生成树被称为无向图 G 的最小生成树
输入格式
第一行包含两个整数 n 和 m 接下来 m 行,每行包含三个整数 u,v,w
表示点 u 和点 v 之间存在一条权值为 w 的边输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible数据范围
1≤n≤105, 1≤m≤2?105
图中涉及边的边权的绝对值均不超过 1000
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
全局变量声明
int n,m,weight=0,k=0;//
int pre[MaxSize];
n端点总数,m边数,weight记录最终答案,k已经连接了多少边
pre数组记录每一位对应的前一级
每一条边的结构体存储声明 、sort比较规则 及 并查集函数
struct node
{///结构体储存边
int from;//起点
int to;//终点
int dis;//权值
}edge[MaxSize];
int Find(int x)
{///查找最高上级
if(pre[x] != x) //还没找到最高上级
return Find(pre[x]);//继续向上查找
return x;
}
bool cmp(const node &a,const node &b)
{///sort排序声明比较规则
return a.dis<b.dis;
}
int FindPro(int x)
{///路径压缩 查找函数优化版
if(pre[x] == x)
return x; //当找到最高上级时结束递归
return pre[x] = FindPro(pre[x]); //找到最高上级并设为对应结点的直接上级
}
void Union(int i,int j)
{///将两个边加入到一个集合中
pre[Find(i)] = Find(j);//将任意一个边的最高上级变成另一条边的下级 这里j的上级作为i的最高上级
}
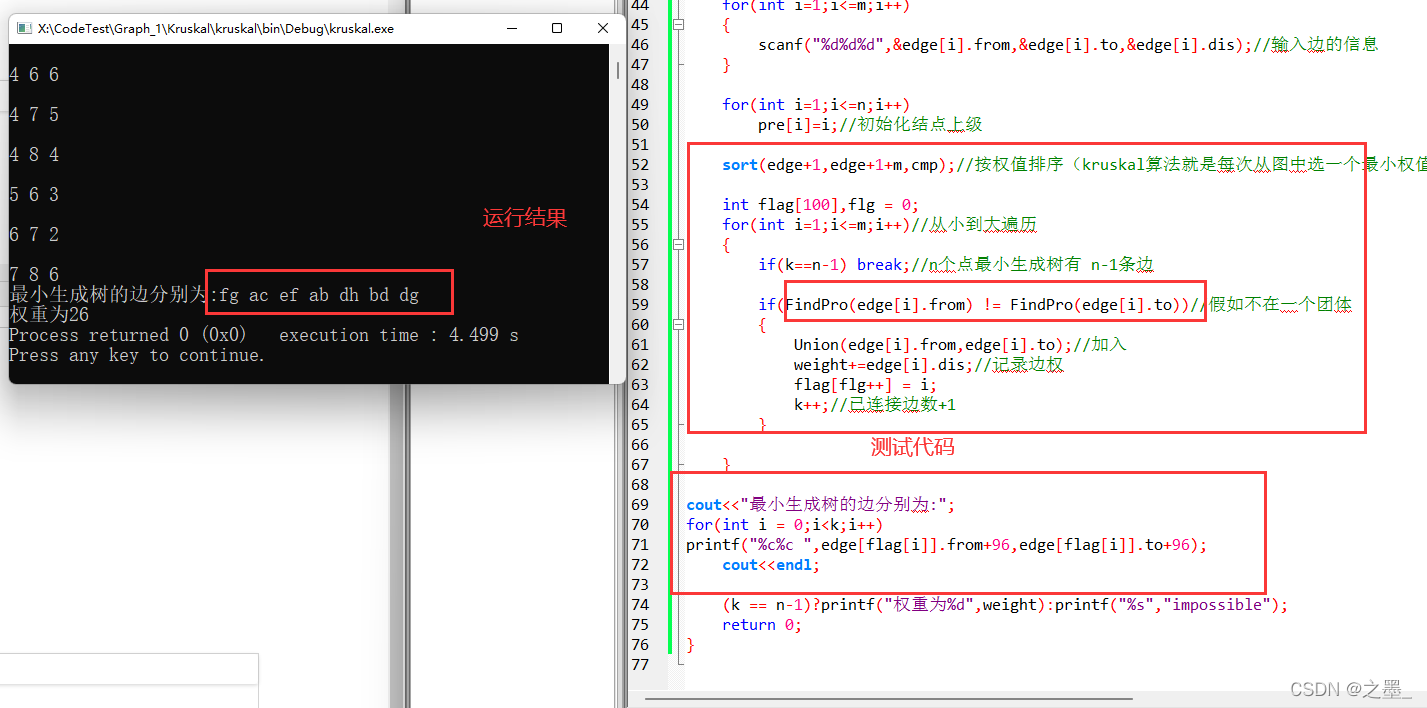
主要测试代码
int main()
{
for(int i=1;i<=n;i++)
pre[i]=i;//初始化结点上级
sort(edge+1,edge+1+m,cmp);//按权值排序(kruskal算法就是每次从图中选一个最小权值的边加入生成树中
for(int i=1;i<=m;i++)//从小到大遍历
{
if(k==n-1) break;//n个点最小生成树只有 n-1条边
if(FindPro(edge[i].from)!=FindPro(edge[i].to))
{//假如两点的上级不是同一个
Union(edge[i].from,edge[i].to);//加入
weight += edge[i].dis;//记录边权
k++;//已连接边数+1
}
}
}
完整代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#define MaxSize 1000
using namespace std;
int n,m,weight=0,k=0;//n端点总数,m边数,weight记录最终答案,k已经连接了多少边
int pre[MaxSize];//记录每一位对应的前一级
struct node
{///结构体储存边
int from;//起点
int to;//终点
int dis;//权值
}edge[MaxSize];
int Find(int x)
{///查找最高上级
if(pre[x] != x) //还没找到最高上级
return Find(pre[x]);//继续向上查找
return x;
}
bool cmp(const node &a,const node &b)
{///sort排序声明比较规则
return a.dis<b.dis;
}
int FindPro(int x)
{///路径压缩 查找函数优化版
if(pre[x] == x)
return x; //当找到最高上级时结束递归
return pre[x] = FindPro(pre[x]); //找到最高上级并设为对应结点的直接上级
}
void Union(int i,int j)
{///将两个边加入到一个集合中
pre[Find(i)] = Find(j);//将任意一个边的最高上级变成另一条边的下级 这里j的上级作为i的最高上级
}
int main()
{
scanf("%d%d",&n,&m);//输入点数,边数
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&edge[i].from,&edge[i].to,&edge[i].dis);//输入边的信息
}
for(int i=1;i<=n;i++)
pre[i]=i;//初始化结点上级
sort(edge+1,edge+1+m,cmp);//按权值排序(kruskal算法就是每次从图中选一个最小权值的边加入生成树中
for(int i=1;i<=m;i++)//从小到大遍历
{
if(k==n-1) break;//n个点最小生成树有 n-1条边
if(FindPro(edge[i].from)!=FindPro(edge[i].to))//假如不在一个团体
{
Union(edge[i].from,edge[i].to);//加入
weight+=edge[i].dis;//记录边权
k++;//已连接边数+1
}
}
printf("%d",weight);
return 0;
}
提交代码时出现了两次错误
一次是 判断最小生成树是否存在
一次是段错误
判断最小生成树是否存在 其实很简单
就是对最后得到的生成树判断它的边k是否==n-1
而段错误就是把存储范围扩大就好了
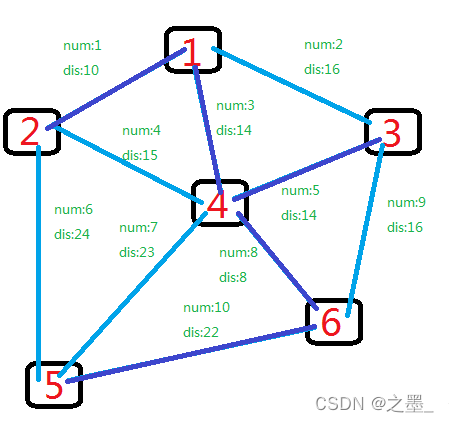
题目二
对下图进行测试 答案正确!
题目三