[数据结构与算法]信息学奥赛一本通 2041：【例5.9】新矩阵

【题目链接】

ybt 2041：【例5.9】新矩阵

【题目考点】

1. 二维数组

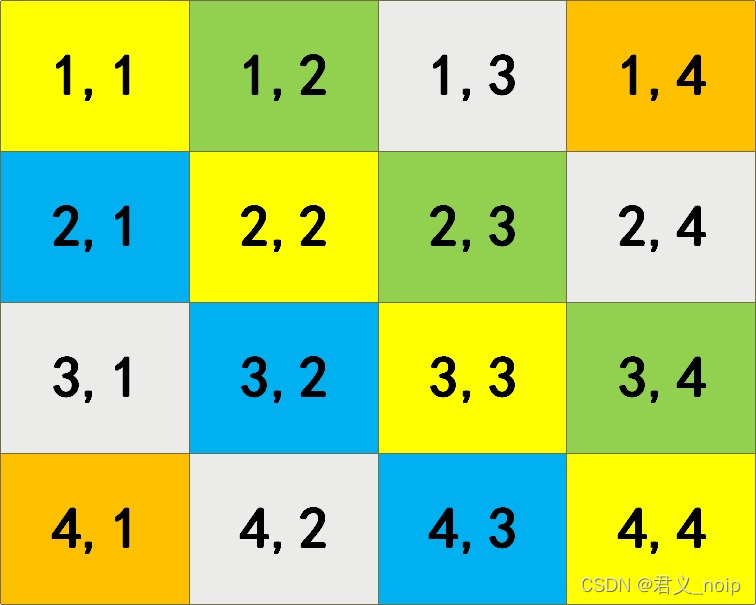
2. 二维数组同一斜线上坐标规律

• 左上右下斜线横纵坐标差值为定值
  
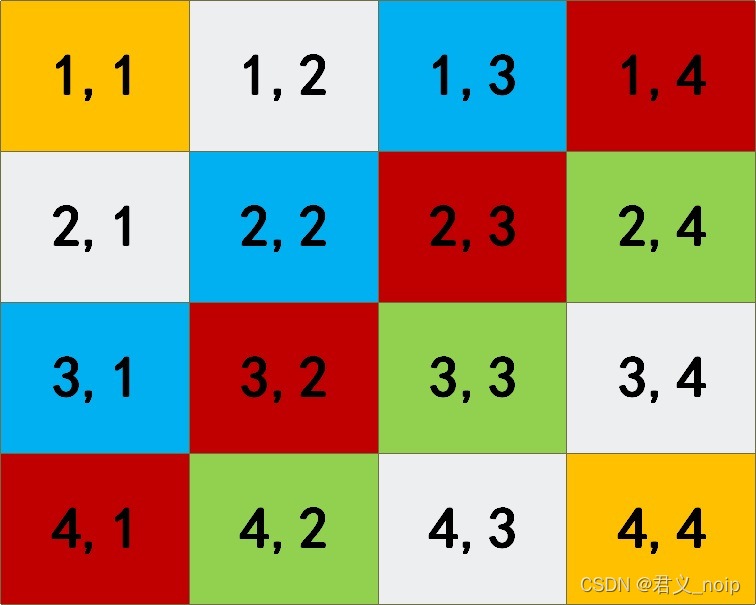
• 右上左下斜线横纵坐标加和为定值
  

【解题思路】

解法1： 利用二维数组中斜线上的坐标规律

在一个n行n列的矩阵上

• 左上右下对角线，经过（1，1）位置，那么这一斜线上各位置行列坐标差值都为0。
• 右上左下对角线，经过（1，n）位置，那么这一斜线上各位置行列坐标加和为1+n

遍历二维数组，只要满足以上两个条件中的其中一个，那么就是对角线上的元素，其值增加10。

解法2： 移动焦点位置，遍历对角线。

• 首先将焦点位置设为（1，1），每次将焦点向右下方移动一次，即行列坐标各加1，每到一个位置，该位置值加10。直到将焦点移出二维数组。
• 将焦点位置设为（1，n），每次将焦点向左下方移动一次，即行坐标加1，列坐标减1。每到一个位置，该位置加10，直到将焦点移出二维数组。
• 为防止两条对角线有重叠部分，可以先在一个各元素都为0的二维数组上面，将对角线位置的值都设为10。如果要向某位置赋值时这里已经有值，那么就不再加10。然后输入二维数组，在已有二维数组基础上，每个位置增加输入的值。

【题解代码】

解法1：利用二维数组中斜线上的坐标规律

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n, a[30][30];
    cin >> n;
    for(int i = 1; i <= n; ++i)//输入矩阵 
        for(int j = 1; j <= n; ++j)
            cin >> a[i][j];
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
        {//左上右下对角线：横纵坐标相同   右上左下对角线：横纵坐标相加和为n+1 
            if(i == j || i+j == n+1)
                a[i][j] += 10; //对角线数字加10        
        }
    for(int i = 1; i <= n; ++i)//输出矩阵 
    {
        for(int j = 1; j <= n; ++j)
            cout << a[i][j] << ' ';
        cout << endl;
    }
    return 0;
}

解法2：移动焦点位置，遍历对角线。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t, n, a[30][30] = {}, i, j;
    cin >> n;
    for(i = j = 1; i <= n && j <= n; i++, j++)//左上右下对角线
        a[i][j] += 10;
    for(i = 1, j = n; i <= n && j >= 1; i++, j--)//右上左下对角线
    {
        if(a[i][j] == 0)//防止重复赋值
            a[i][j] += 10;
    }
    for(int i = 1; i <= n; ++i)//输入矩阵 
        for(int j = 1; j <= n; ++j)
        {
            cin >> t;
            a[i][j] += t;
        }
    for(int i = 1; i <= n; ++i)//输出矩阵 
    {
        for(int j = 1; j <= n; ++j)
            cout << a[i][j] << ' ';
        cout << endl;
    }
    return 0;
}