[数据结构与算法]leetcode(力扣)上如何自己构造二叉树输入用例？（python写法）

目录

• 1、题目描述：
• 2、自己构造输入输出：

面试的时候，面试官考了一道二叉树的题，让我们自己构造输入输出（白板，也叫ACM模式），然后发现题不难，但是不会构造输入输出，人傻了，本文基于这个问题，做一个解答。

我们还是拿一道题来说说：
leetcode第515题：https://leetcode-cn.com/problems/find-largest-value-in-each-tree-row/

1、题目描述：

2、自己构造输入输出：

从二叉树 推导到 序列，大家可以发现这就是层序遍历。

但从序列 推导到 二叉树，很多同学就看不懂了，这得怎么转换呢。

二叉树可以有两种存储方式，一种是 链式存储，另一种是顺序存储。

• 链式存储，就是大家熟悉的二叉树，用指针指向左右孩子。

• 顺序存储，就是用一个数组来存二叉树，其方式如图所示：

那么此时我们应该知道，数组如何转化成 二叉树了。如果父节点的数组下标是$i$，那么它的左孩子下标就是$i?2+1$，右孩子下标就是 $i?2+2$。计算过程为：

如果父节点在第$k$层，第$m,m\in [0,2^k]$个节点，则其左孩子所在的位置必然为$k+1$层，第$2?(m?1)+1$个节点。

计算父节点在数组中的索引： $$inde{x}_{father}=(\sum _{i=0}^{i=k?1}{2}^i)+m?1=2^k?1+m?1$$

计算左子节点在数组的索引： $$inde{x}_{left}=(\sum _{i=0}^{i=k}{2}^i)+2?m?1?1=2^{k+1}+2m?3$$

故左孩子的下表为$inde{x}_{left}=inde{x}_{father}\times 2+1$，同理可得到右子孩子的索引关系。也可以直接在左子孩子的基础上+1。

但是代码咋写呢？

具体过程看注释：

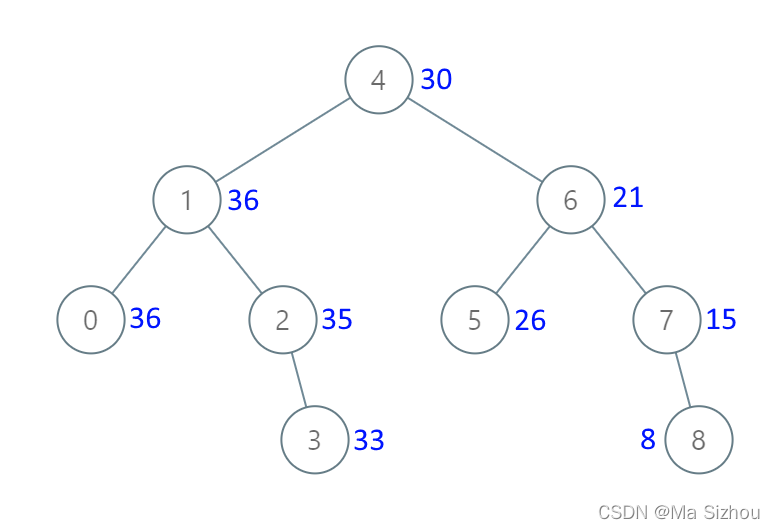
我们以下面这个二叉树为例子：
传入的序列为：[4,1,6,0,2,5,7,None,None,None,3,None,None,None,8]
二叉树长这样：

class Tree:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

    def max_value(self, root):
        """这道题的题解：层序遍历"""
        res = [] # 保存每一层的最大值
        import collections
        q = collections.deque()
        q.append(root) # 根节点入队
        
        while q:
            size = len(q)
            _max = q[0].val # 把同层的第一个作为最大值
            
            for _ in range(size):
                cur = q.popleft()
                if _max < cur.val:
                    _max = cur.val
                
                if cur.left: q.append(cur.left)
                if cur.right: q.append(cur.right)
                # print(cur.val, end=" ")
            res.append(_max)

        return res

def construct_binary_tree(nums):
    """根据数组构造二叉树"""
    Treelist = [None for _ in range(len(nums))]
    # 把输入数值数组，先转化为二叉树节点数组
    for i in range(len(nums)):
        if nums[i] != None:
            node = Tree(nums[i])
            Treelist[i] = node
        if i == 0: root = node
    # 遍历一遍，根据规则左右孩子赋值就可以了
    # 注： 结束规则是 i * 2 + 2 < len(nums
    i = 0
    while i * 2 + 2 < len(nums):
        if Treelist[i] != None:
            # 线性存储转连式存储关键逻辑
            Treelist[i].left = Treelist[i * 2 + 1]
            Treelist[i].right = Treelist[i * 2 + 2]
        i += 1
    
    return root # 返回根节点
    

nums = [4,1,6,0,2,5,7,None,None,None,3,None,None,None,8] # 输入一个序列
root = construct_binary_tree(nums) # 构造二叉树

res = root.max_value(root) # 本题题解

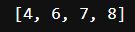
print(res) # 打印对比结果

输出：