[数据结构与算法] SM4密码算法实现(C语言只使用stdio.h库)

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> SM4密码算法实现(C语言只使用stdio.h库) -> 正文阅读

[数据结构与算法]SM4密码算法实现(C语言只使用stdio.h库)

SM4算法分析与实现

SM4密码算法是一个分组算法。数据分组长度为128比特，密钥长度为128比特。加密算法与密钥扩展算法都采用32轮迭代结构。SM4密码算法以字节（8位）和字（32位）为单位进行数据处理。SM4密码算法是对合运算，因此解密算法与加密算法相同，只是轮密钥的使用顺序相反，解密轮密钥是加密轮密钥的逆序。

SM4算法原理

基本运算
SM4密码算法使用模2加和循环移位作为基本运算。
- 模2加：⊕，32位异或运算
- 循环移位：<<< i，把32位字循环左移i位。

基本密码部件

S盒

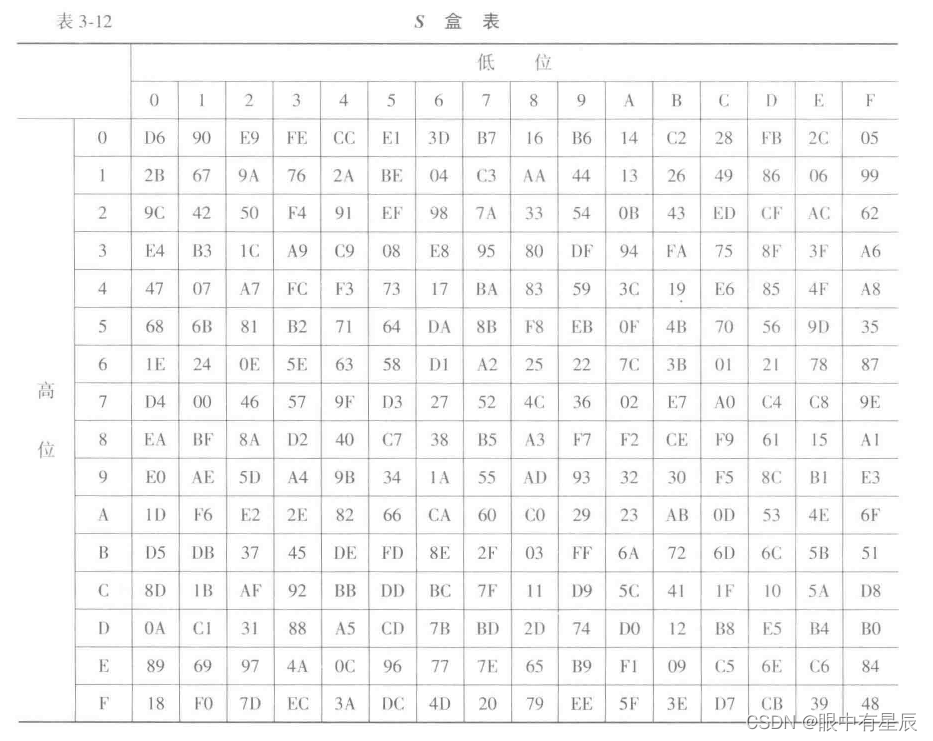
SM4的S盒是一种以字节为单位的非线性代替变换，其密码学的作用起混淆作用。S盒的输入和输出都是8位的字节，它本质上是8位的非线性置换。设输入字节为a，输出字节为b，则S盒的运算可表示为：
$b = S b o x (a)$
S盒的代替规则如下表所示。例如，设S盒的输入为EF，则5盒的输出为表中第E行与第F列交点处的值84，即Sbox(EF)= 84。
非线性变换τ

SM4的非线性变换τ是一种以字为单位的非线性代替变换。它由4个S盒并置构成。本质上它是S盒的一种并行应用。

设输入字为A＝(a₀，a₁，a₂，a₃），输出字为B＝(b₀，b₁，b₂，b₃)，则
$B=τ(A)=(Sbox(a_0)，Sbox(a_1)，Sbox(a_2)，Sbox(a_3))$
线性变换部件L

线性变换部件L是以字为处理单位的线性变换部件，其输入输出都是32位的字。其密码学的作用是起扩散的作用。
设L的输入为字B，输出为字C，则
$C = L (B) = B \oplus (B < < < 2) \oplus (B < < < 10) \oplus (B < < < 18) \oplus (B < < < 24)$
合成变换T

合成变换T由非线性变换τ和线性变换L复合而成，数据处理的单位是字。设输入为字，则先对X进行非线性τ变换，再进行线性L变换。记为
$T (X) = L (τ (X))$
由于合成变换T是非线性变换τ和线性变换L的复合，所以它综合起到混淆和扩散的作用，从而可提高密码的安全性。

轮函数
SM4密码算法采用对基本轮函数进行迭代的结构。利用上述基本密码部件，便可构成轮函数。SM4密码算法的轮函数是一种以字为处理单位的密码函数。
设轮函数F的输入为(X₀，X₁，X₂，X₃)，四个32位字，共128位。轮密钥为RK，RK也是一个32位的字。轮函数F的输出也是一个32位的字。轮函数F的运算如下：
$F(X_0，X_1，X_2，X_3，RK)= X_0 ⊕ T(X_1 ⊕ X_2 ⊕ X_3 ⊕ RK)$

加密算法

SM4密码算法是一个分组算法。数据分组长度为128比特，密钥长度为128比特。加密算法采用32轮迭代结构，每轮使用一个轮密钥。
设输入明文为(X₀，X₁，X₂，X₃)，四个字，共128位。输入轮密钥为RK_i，i＝0,1,…,31，共32个字。输出密文为(Y₀，Y₁，Y₂，Y₃)，四个字，128位。则加密算法可描述如下:
$X_{i+4}=F(X_1，X_{i+1}，X_{i+2}，X_{i+3}，RKi)\\=X_i⊕T(X_{i+1}⊕X_{i+2}⊕X_{i+3}⊕RK_i),~i=0,1,...,31$
为了与解密算法需要的顺序一致，同时也与人们的习惯顺序一致，在加密算法之后还需要一个反序处理R：
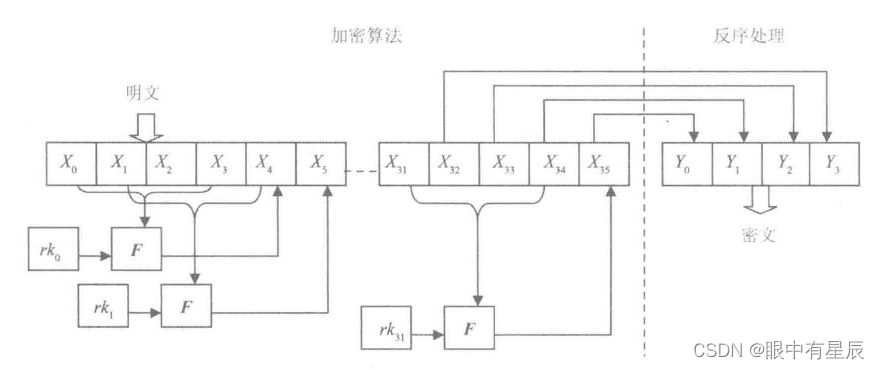
$R(Y_0，Y_1，Y_2，Y_3) = (X_{35}，X_{34}，X_{33}，X_{32})$

加密算法的框图如图所示。

在这里插入图片描述

解密算法

SM4密码算法是对合运算，因此解密算法与加密算法相同，只是轮密钥的使用顺序相反，解密轮密钥是加密轮密钥的逆序。
设输入密文为(Y₀，Y₁，Y₂，Y₃)，输入轮密钥为RK_i，i=31,30,…1, 0，输出明文为(M₀，M₁，M₂，M₃)，根据加密算法的R(Y₀，Y₁，Y₂，Y₃) = (X₃₅，X₃₄，X₃₃，X₃₂)，为了方便与加密算法对照，在解密算法中仍然采用Xi表示密文。于是可得到如下的解密算法：
$X = F(X_{i+4}，X_{i+3}，X_{i+2}，X_{i+1}，RK_i)\\ =X_{i+4} ⊕ T(X_{i+3} ⊕ X_{i+2} ⊕ X_{i+1} ⊕ RK_i), i=31,30,...,1,0$
与加密算法之后需要一个反序处理同样的道理，在解密算法之后也需要一个反序处理R：
$R(M_0，M_1，M_2，M_3) = (X_3，X_2，X_1，X_0)$

密钥扩展算法
SM4 密码算法使用128位的加密密钥，并采用32轮迭代加密结构，每一轮加密使用一个32位的轮密钥，共使用32个轮密钥。因此需要使用密钥扩展算法，从加密密钥产生出32个轮密钥。
常数FK
在密钥扩展中使用如下的常数：
FK₀ = (A3B1BAC6)，FK₁ = (56AA3350)，FK₂ = (677D9197)，FK₃ = (B27022DC)
固定参数CK
共使用32个固定参数如下（16进制）：

0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279

密钥扩展算法
设输入加密密钥为MK(MK₀，MK₁，MK₂，MK₃),输出轮密钥为RK_i， i=0,1,…,30,31，中间数据为K_i，i = 0,1,…,34,35，则密钥扩展算法可描述如下：
$①(K_0，K_1，K_2，K_3) = (MK_0 ⊕ FK_0, MK_1 ⊕ FK_1，MK_2 ⊕ FK_2，MK_3 ⊕ FK_3) \\ ②For~i = 0,1,...,30,31~Do~RK = Ki ⊕ T’(K_{i+1}，K_{i+2}，K_{i+3}，CK_i)$
说明：其中的T’变换与加密算法轮函数中的T基本相同，只将其中的线性变换L修改为以下的L’：
$L ’ (B) = B \oplus (B < < < 13) \oplus (B < < < 23)$

SM4代码实现和测试

编程语言

采用C语言，只使用了C语言库的stdio.h。
运行环境

Windows10平台下的Dev-CPP5.11。

主要函数

u32 functionB(u32 b); // 查S盒的函数B 
u32 loopLeft(u32 a, short length); // 循环左移函数 
u32 functionL1(u32 a); // 线性变换L
u32 functionL2(u32 a); // 线性变换L'
u32 functionT(u32 a, short mode); // 合成变换T
void extendFirst(u32 MK[], u32 K[]); // 密钥扩展算法第一步
void extendSecond(u32 RK[], u32 K[]); // 密钥扩展算法第二步
void getRK(u32 MK[], u32 K[], u32 RK[]); // 轮密钥获取算法
void iterate32(u32 X[], u32 RK[]); // 迭代算法
void reverse(u32 X[], u32 Y[]); // 反转函数 
void encryptSM4(u32 X[], u32 RK[], u32 Y[]); // 加密算法
void decryptSM4(u32 X[], u32 RK[], u32 Y[]); // 解密算法

3.1 查询S盒的函数B

/*
  查S盒的函数B 
  参数: u32 b
  返回值:  查S盒的结果u32 b
*/ 
u32 functionB(u32 b) {
  u8 a[4];
  short i;
  a[0] = b / 0x1000000;
  a[1] = b / 0x10000;
  a[2] = b / 0x100;
  a[3] = b;
  b = Sbox[a[0]] * 0x1000000 + Sbox[a[1]] * 0x10000 + Sbox[a[2]] * 0x100 + Sbox[a[3]];
  return b;
}

3.2 循环左移算法

/*
  循环左移算法
  参数： u32 a  length：循环左移位数
  返回值：u32 b
*/
u32 loopLeft(u32 a, short length) {
  short i;
  for(i = 0; i < length; i++) {
   	a = a * 2 + a / 0x80000000;
  }
  return a;
}

3.3 密钥线性变换函数L

/* 
  密钥线性变换函数L
  参数： u32 a
  返回值：线性变换后的u32 a 
*/
u32 functionL1(u32 a) {
  return a ^ loopLeft(a, 2) ^ loopLeft(a, 10) ^ loopLeft(a, 18) ^ loopLeft(a, 24);
}

3.4 密钥线性变换函数L’

/* 
  密钥线性变换函数L'
  参数： u32 a
  返回值：移位操作后的u32 a 
*/
u32 functionL2(u32 a) {
  return a ^ loopLeft(a, 13) ^ loopLeft(a, 23);
}

3.5 合成变换T

/*
  合成变换T
  参数： u32 a  short mode：1表示明文的T，调用L；2表示密钥的T，调用L' 
  返回值：合成变换后的u32 a 
*/
u32 functionT(u32 a, short mode) {
  return mode == 1 ? functionL1(functionB(a)) : functionL2(functionB(a));
}

3.6 密钥扩展算法第一步

/* 
  密钥扩展算法第一步
  参数： MK[4]：密钥 K[4]:中间数据，保存结果  （FK[4]：常数） 
  返回值：无 
*/ 
void extendFirst(u32 MK[], u32 K[]) {
  int i;
  for(i = 0; i < 4; i++) {
     K[i] = MK[i] ^ FK[i]; 
  } 
}

3.7 密钥扩展算法第二步

/* 
  密钥扩展算法第二步
  参数： RK[32]：轮密钥，保存结果  K[4]：中间数据 （CK[32]：固定参数） 
  返回值：无
*/ 
void extendSecond(u32 RK[], u32 K[]) {
  short i;
  for(i = 0; i <32; i++) {
     K[(i+4)%4] = K[i%4] ^ functionT(K[(i+1)%4] ^ K[(i+2)%4] ^ K[(i+3)%4] ^ CK[i], 2);
     RK[i] = K[(i+4)%4];
  } 
}

3.8 密钥扩展算法

/*
  密钥扩展算法 
  参数： MK[4]：密钥   K[4]：中间数据  RK[32]：轮密钥，保存结果 
  返回值：无 
*/ 
void getRK(u32 MK[], u32 K[], u32 RK[]) {
  extendFirst(MK, K);
  extendSecond(RK, K);
}

3.9 迭代算法

/*
  迭代32次
  参数： u32 X[4]：迭代对象，保存结果  u32 RK[32]：轮密钥
  返回值：无   
*/
void iterate32(u32 X[], u32 RK[]) {
  short i;
  for(i = 0; i < 32; i++) {
     X[(i+4)%4] = X[i%4] ^ functionT(X[(i+1)%4] ^ X[(i+2)%4] ^ X[(i+3)%4] ^ RK[i], 1);
  }
}

3.10 反转函数

/*
  反转函数 
  参数； u32 X[4]：反转对象  u32 Y[4]：反转结果
  返回值：无 
*/
void reverse(u32 X[], u32 Y[]) {
   short i;
   for(i = 0; i < 4; i++){
    Y[i] = X[4 - 1 - i];
   } 
}

3.11 加密算法

/*
  加密算法
  参数： u32 X[4]：明文  u32 RK[32]：轮密钥  u32 Y[4]：密文，保存结果 
  返回值：无 
*/
void encryptSM4(u32 X[], u32 RK[], u32 Y[]) {
  iterate32(X, RK);
  reverse(X, Y);
}

3.12 解密算法

/*
  解密算法
  参数：   u32 X[4]：密文  u32 RK[32]：轮密钥  u32 Y[4]：明文，保存结果
  返回值：无 
*/
void decryptSM4(u32 X[], u32 RK[], u32 Y[]) {
  short i;
  u32 reverseRK[32];
  for(i = 0; i < 32; i++) {
     reverseRK[i] = RK[32-1-i];
  }
  iterate32(X, reverseRK);
  reverse(X, Y);
}

测试数据

数据来自《密码学引论》第三版武汉大学出版社中关于SM4算法的描述。

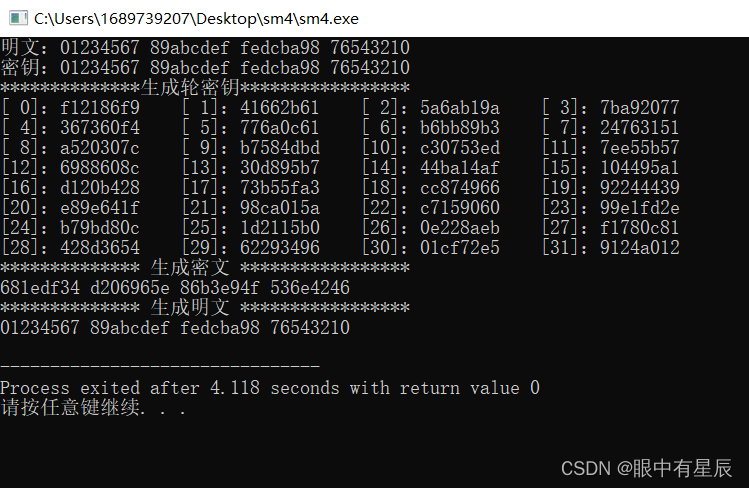
明文：	01234567 89abcdef fedcba98 76543210
密钥：	01234567 89abcdef fedcba98 76543210
密文：	681edf34 d206965e 86b3e94f 536e4246

测试结果

在这里插入图片描述

完整代码

#include<stdio.h>
#define u8 unsigned char
#define u32 unsigned long

// S盒
const u8 Sbox[256] = {
	0xd6,0x90,0xe9,0xfe,0xcc,0xe1,0x3d,0xb7,0x16,0xb6,0x14,0xc2,0x28,0xfb,0x2c,0x05,
	0x2b,0x67,0x9a,0x76,0x2a,0xbe,0x04,0xc3,0xaa,0x44,0x13,0x26,0x49,0x86,0x06,0x99,
	0x9c,0x42,0x50,0xf4,0x91,0xef,0x98,0x7a,0x33,0x54,0x0b,0x43,0xed,0xcf,0xac,0x62,
	0xe4,0xb3,0x1c,0xa9,0xc9,0x08,0xe8,0x95,0x80,0xdf,0x94,0xfa,0x75,0x8f,0x3f,0xa6,
	0x47,0x07,0xa7,0xfc,0xf3,0x73,0x17,0xba,0x83,0x59,0x3c,0x19,0xe6,0x85,0x4f,0xa8,
	0x68,0x6b,0x81,0xb2,0x71,0x64,0xda,0x8b,0xf8,0xeb,0x0f,0x4b,0x70,0x56,0x9d,0x35,
	0x1e,0x24,0x0e,0x5e,0x63,0x58,0xd1,0xa2,0x25,0x22,0x7c,0x3b,0x01,0x21,0x78,0x87,
	0xd4,0x00,0x46,0x57,0x9f,0xd3,0x27,0x52,0x4c,0x36,0x02,0xe7,0xa0,0xc4,0xc8,0x9e,
	0xea,0xbf,0x8a,0xd2,0x40,0xc7,0x38,0xb5,0xa3,0xf7,0xf2,0xce,0xf9,0x61,0x15,0xa1,
	0xe0,0xae,0x5d,0xa4,0x9b,0x34,0x1a,0x55,0xad,0x93,0x32,0x30,0xf5,0x8c,0xb1,0xe3,
	0x1d,0xf6,0xe2,0x2e,0x82,0x66,0xca,0x60,0xc0,0x29,0x23,0xab,0x0d,0x53,0x4e,0x6f,
	0xd5,0xdb,0x37,0x45,0xde,0xfd,0x8e,0x2f,0x03,0xff,0x6a,0x72,0x6d,0x6c,0x5b,0x51,
	0x8d,0x1b,0xaf,0x92,0xbb,0xdd,0xbc,0x7f,0x11,0xd9,0x5c,0x41,0x1f,0x10,0x5a,0xd8,
	0x0a,0xc1,0x31,0x88,0xa5,0xcd,0x7b,0xbd,0x2d,0x74,0xd0,0x12,0xb8,0xe5,0xb4,0xb0,
	0x89,0x69,0x97,0x4a,0x0c,0x96,0x77,0x7e,0x65,0xb9,0xf1,0x09,0xc5,0x6e,0xc6,0x84,
	0x18,0xf0,0x7d,0xec,0x3a,0xdc,0x4d,0x20,0x79,0xee,0x5f,0x3e,0xd7,0xcb,0x39,0x48
};
	
// 密钥扩展算法的常数FK 
const u32 FK[4] = {
	0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc
};

// 密钥扩展算法的固定参数CK 
const u32 CK[32] = {
	0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
	0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
	0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
	0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
	0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
	0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
	0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
	0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
};

u32 functionB(u32 b); // 查S盒的函数B 
u32 loopLeft(u32 a, short length); // 循环左移函数 
u32 functionL1(u32 a); // 线性变换L
u32 functionL2(u32 a); // 线性变换L'
u32 functionT(u32 a, short mode); // 合成变换T
void extendFirst(u32 MK[], u32 K[]); // 密钥扩展算法第一步
void extendSecond(u32 RK[], u32 K[]); // 密钥扩展算法第二步
void getRK(u32 MK[], u32 K[], u32 RK[]); // 轮密钥获取算法
void iterate32(u32 X[], u32 RK[]); // 迭代算法
void reverse(u32 X[], u32 Y[]); // 反转函数 
void encryptSM4(u32 X[], u32 RK[], u32 Y[]); // 加密算法
void decryptSM4(u32 X[], u32 RK[], u32 Y[]); // 解密算法
 
/*
	查S盒的函数B 
	参数:	u32 b
	返回值:	查S盒的结果u32 b
*/ 
u32 functionB(u32 b) {
	u8 a[4];
	short i;
	a[0] = b / 0x1000000;
	a[1] = b / 0x10000;
	a[2] = b / 0x100;
	a[3] = b;
	b = Sbox[a[0]] * 0x1000000 + Sbox[a[1]] * 0x10000 + Sbox[a[2]] * 0x100 + Sbox[a[3]];
	return b;
}

/*
	循环左移算法
	参数：	u32 a    length：循环左移位数
	返回值：u32 b 
*/
u32 loopLeft(u32 a, short length) {
	short i;
	for(i = 0; i < length; i++) {
		a = a * 2 + a / 0x80000000;
	}
	return a;
}

/* 
	密钥线性变换函数L
	参数：	u32 a
	返回值：线性变换后的u32 a	
*/
u32 functionL1(u32 a) {
	return a ^ loopLeft(a, 2) ^ loopLeft(a, 10) ^ loopLeft(a, 18) ^ loopLeft(a, 24);
}

/* 
	密钥线性变换函数L'
	参数：	u32 a
	返回值：移位操作后的u32 a	
*/
u32 functionL2(u32 a) {
	return a ^ loopLeft(a, 13) ^ loopLeft(a, 23);
}

/*
	合成变换T
	参数：	u32 a    short mode：1表示明文的T，调用L；2表示密钥的T，调用L' 
	返回值：合成变换后的u32 a 
*/
u32 functionT(u32 a, short mode) {
	return mode == 1 ? functionL1(functionB(a)) : functionL2(functionB(a));
}
 
/* 
	密钥扩展算法第一步
	参数：	MK[4]：密钥  K[4]:中间数据，保存结果	（FK[4]：常数） 
	返回值：无 
*/ 
void extendFirst(u32 MK[], u32 K[]) {
	int i;
	for(i = 0; i < 4; i++) {
		K[i] = MK[i] ^ FK[i]; 
	} 
}

/* 
	密钥扩展算法第二步
	参数：	RK[32]：轮密钥，保存结果    K[4]：中间数据 （CK[32]：固定参数） 
	返回值：无
*/ 
void extendSecond(u32 RK[], u32 K[]) {
	short i;
	for(i = 0; i <32; i++) {
		K[(i+4)%4] = K[i%4] ^ functionT(K[(i+1)%4] ^ K[(i+2)%4] ^ K[(i+3)%4] ^ CK[i], 2);
		RK[i] = K[(i+4)%4];
	} 
}

/*
	密钥扩展算法 
	参数：	MK[4]：密钥     K[4]：中间数据    RK[32]：轮密钥，保存结果 
	返回值：无 
*/ 
void getRK(u32 MK[], u32 K[], u32 RK[]) {
	extendFirst(MK, K);
	extendSecond(RK, K);
}

/*
	迭代32次
	参数：	u32 X[4]：迭代对象，保存结果    u32 RK[32]：轮密钥
	返回值：无	  
*/
void iterate32(u32 X[], u32 RK[]) {
	short i;
	for(i = 0; i < 32; i++) {
		X[(i+4)%4] = X[i%4] ^ functionT(X[(i+1)%4] ^ X[(i+2)%4] ^ X[(i+3)%4] ^ RK[i], 1);
	}
}

/*
	反转函数 
	参数；	u32 X[4]：反转对象    u32 Y[4]：反转结果
	返回值：无 
*/
void reverse(u32 X[], u32 Y[]) {
	 short i;
	 for(i = 0; i < 4; i++){
	 	Y[i] = X[4 - 1 - i];
	 } 
} 

/*
	加密算法
	参数：	u32 X[4]：明文    u32 RK[32]：轮密钥    u32 Y[4]：密文，保存结果 
	返回值：无 
*/
void encryptSM4(u32 X[], u32 RK[], u32 Y[]) {
	iterate32(X, RK);
	reverse(X, Y);
} 

/*
	解密算法
	参数： 	u32 X[4]：密文    u32 RK[32]：轮密钥    u32 Y[4]：明文，保存结果
	返回值：无 
*/
void decryptSM4(u32 X[], u32 RK[], u32 Y[]) {
	short i;
	u32 reverseRK[32];
	for(i = 0; i < 32; i++) {
		reverseRK[i] = RK[32-1-i];
	}
	iterate32(X, reverseRK);
	reverse(X, Y);
}
 
/*
	测试数据：
	明文：	01234567 89abcdef fedcba98 76543210
	密钥：	01234567 89abcdef fedcba98 76543210
	密文：	681edf34 d206965e 86b3e94f 536e4246 
*/
int main(void) {
	u32 X[4]; // 明文 
	u32 MK[4]; // 密钥 
	u32 RK[32]; // 轮密钥  
	u32 K[4]; // 中间数据 
	u32 Y[4]; // 密文 
	short i; // 临时变量 
	printf("明文："); 
	scanf("%8x%8x%8x%8x", &X[0], &X[1], &X[2], &X[3]);
	printf("密钥："); 
	scanf("%8x%8x%8x%8x", &MK[0], &MK[1], &MK[2], &MK[3]);
	printf("**************生成轮密钥*****************\n"); 
	getRK(MK, K, RK);
	for(i = 0; i < 32; i++) {
		printf("[%2d]：%08x    ", i, RK[i]);
		if(i%4 == 3)	printf("\n"); 
	}
	printf("************** 生成密文 *****************\n"); 
	encryptSM4(X, RK, Y);
	printf("%08x %08x %08x %08x\n", Y[0], Y[1], Y[2], Y[3]);
	printf("************** 生成明文 *****************\n");  
	decryptSM4(Y, RK, X);
	printf("%08x %08x %08x %08x\n", X[0], X[1], X[2], X[3]);
	return 0;	
}