图的最小生成树
完全图:任意两个顶点之间都有直达的边相连的无向图。
连通图:任意两个顶点之间都有路径相通的无向图。
生成树:一个连通图的生成树是指一个极小连通子图,含有图中的全部n个顶点,但只有足以构成一棵树的n-1条边。
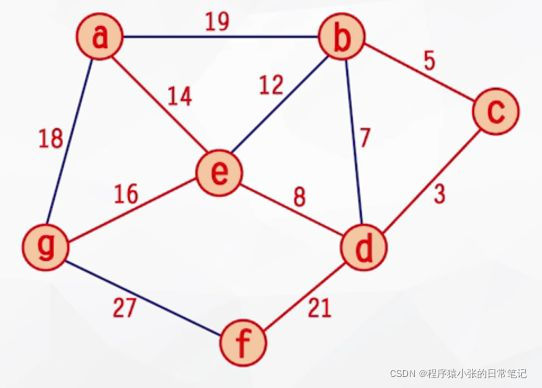
构造网的一棵最小生成树,即:在e条带权的边中选取n-1条边(不构成回路),使"权值之和"为最小。
最小生成树要解决的两个问题;
-
尽可能选取权值小的边,但不能构成回路。
-
选取n-1条恰当的边以连接网的n个顶点。
算法1:普里姆(Prim)算法
普里姆(Prim)算法基本思想:
取图中任意一个顶点v作为生成树的根,之后往生成树上添加新的顶点w。**在添加的顶点w和已经在生成树上的顶点v之间必定存在一条边,该边的权值在所有连通顶点v和w之间的边中取值最小。**之后继续往生成树上添加顶点,直到生成树上含有n个顶点为止。
一般情况下所添加的顶点应满足条件:
在生成树的构造过程中,图中n个顶点分属两个集合:已落在生成树上的顶点集U和尚未落在生成树上的顶点集V-U;则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。
普里姆(Prim)算法实现:
连通网用带权的邻接矩阵表示,并设置一个**辅助数组closedge[ ],**数组元素下标对应当前V-U集中的顶点序号,**元素值则记录该顶点和U集合中相连接的代价最小(最近)边的顶点序号adjvex和权值lowcost。**即对v属于V-U的每个顶点,closedge[v]记录所有与v邻接的,从U到V-U的那组边中的最小边信息。

算法演示过程:
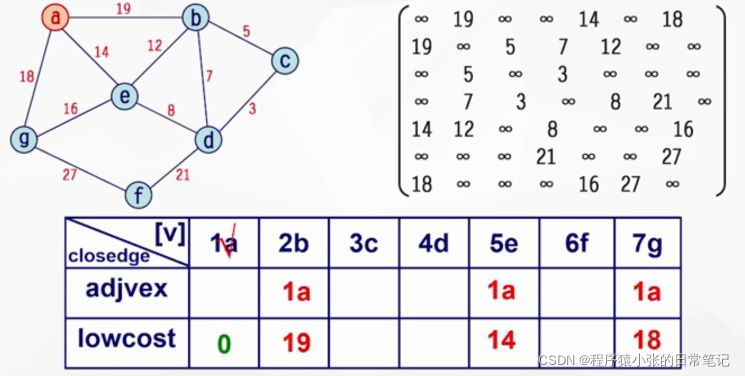
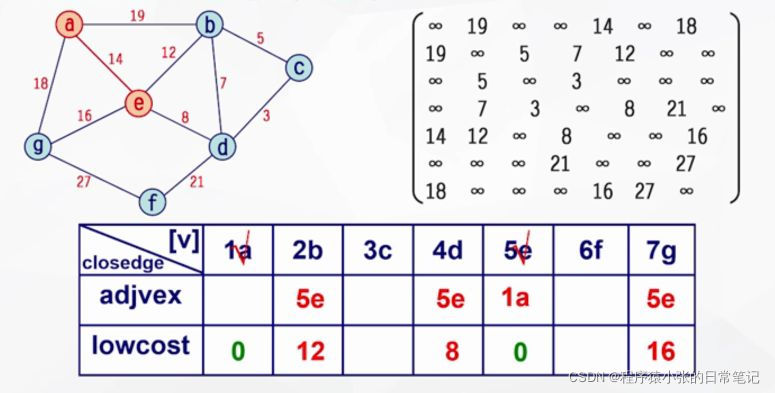
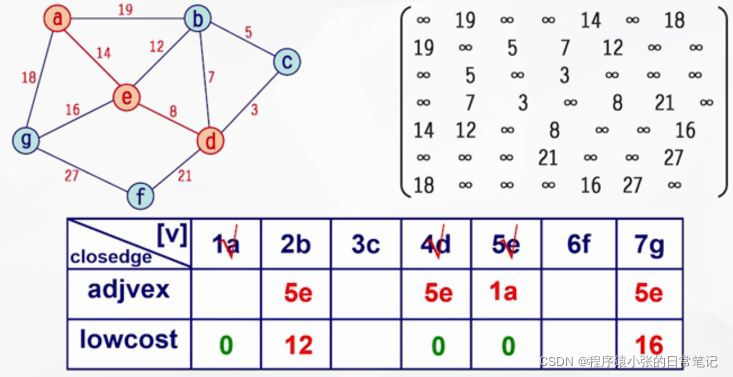
依次重复上述操作:直至
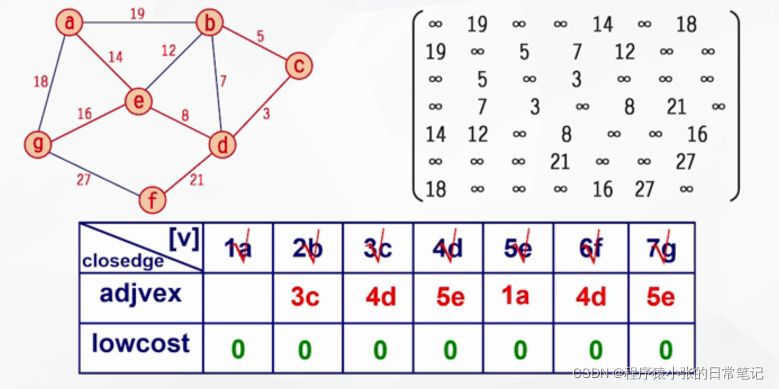
代码实现:
struct
{
vertexData adjvex;
int lowcost;
}closedge[MAX_VERTEX_NUM];
MiniSpanTree_Prim(AdjMatrix gn,VertexData u)
{
k=LocateVertex(gn,v);
closedge[k].lowcost=0;
for(i=0;i<gn.vexnum;i++)
if(i!=k){
colsedge[i].adjvex=u;
closedge[i].lowcost=gn.arcs[k][i].adj;
}
for(e=1;e<=gn.vexnum-1;e++)
{
k0=Minium(closedge);
u0=closedge[k0].adjvex;
v0=gn.vexs[k0];
printf(u0,v0);
closedge[k0].lowcost=0;
for(i=0;i<vexnum;i++)
if(gn.arcs[k0][i].adj<closedge[i].lowcost)
{
closedge[i].lowcost = gn.arcs[k0][i].adj;
closedge[i].adjvex = v0;
}
}
}
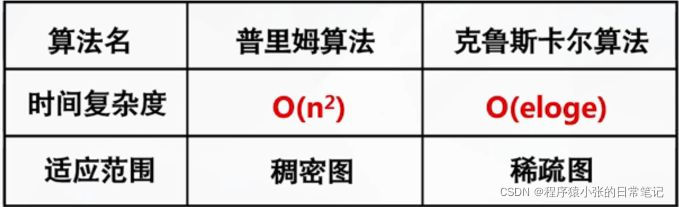
时间复杂度(n*n)
适合于稠密图(顶点少,边数多)
算法2:克鲁斯卡尔(Kruskal)算法
又称加边法。
问题的出发点:为使生成树上边的权值之和达到最小,则应使生成树中每一条边的权值尽可能地小。
具体做法:先构造一个只含n个顶点的子图SG,然后从权值最小的边开始,若它的添加不使SG中产生回路则在SG上加上这条边,如此重复,直至加上n-1条边为止。
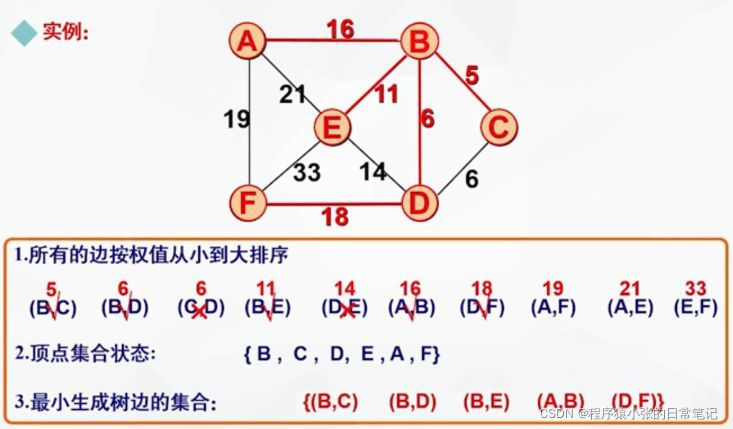
代码实现主要问题:
- 权值排序(堆排序)
- 判断图中有没有回路生成
暂时不做实现!!!
总结:
图的生成树不唯一,从不同的顶点出发进行遍历,可以得到不同的生成树。
即使从相同的顶点出发,在选择最小边时,可能有多条同样的边可选,此时任选其一。