[数据结构与算法]POJ-2286 The Rotation Game + Python(DFS)

题目链接：poj 2286 The Rotation Game-面试哥

题目目的：通过沿8个方向旋转，使得中间8个元素的数值相同，示例如下：

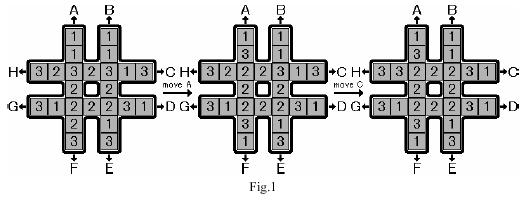
?一?解题说明

#1 注意事项：Rotation时，需要重新赋值矩阵数据，否则将前后一起变化。
#2 注意事项：用队列存储操作过程，在将队列赋值给新队列时，需要特别注意队列中的元素顺序，因为它对应着操作顺序。

? ? ? ? ? ? ? ?  new_step = []
? ? ? ? ? ? ? ?  new_step.append(dir_i)
? ? ? ? ? ? ? ?  for step_i in step:
? ? ? ? ? ? ? ?  ? ? new_step.append(step_i)
? ? ? ? ? ? ? ?  # 要保证顺序不能变，否则最终输出时，顺序将有误
? ? ? ? ? ? ? ?  new_step.append(dir_i) # 在尾部添加
? ? ? ? ? ? ? ?  # 并将头部的数据去除
? ? ? ? ? ? ? ?  new_step.pop(0)

# 提前设置各操作对应的数字：
# 设置操作标志
action = {0:['A'],1:['B'],2:['C'],3:['D'],4:['E'],5:['F'],6:['G'],7:['H']}

#3 目标元素的确定：统计1/2/3三个元素在目标区域中的个数，以个数最大者对应的元素为目标元素，见findTarget函数
#4 一些法则：
#4.1 旋转一次之后，如果目标元素发生了变化(例如由2变成了3)，则return
#4.2 旋转一次之后，如果目标元素未发生变化，但数量减少，则return
#4.3 旋转一次之后，如果目标元素未发生变化，并且数量未减少，则进入下一次dfs搜索；
#5 终止条件
#5.1 目标区域中的目标元素的个数为8，成功return！
#5.1.1 保存当前方案
#5.1.2 存储当前的目标元素
#5.2 如果DFS搜索深度大于设定值，则错误return。
#5.3 假设当前目标元素能够找到可行的方案，则不再对其他目标元素进行搜索。
#5.4 对当前目标元素的所有方案进行分析，选择长度最短、按字母顺序排序的方案。
#5.4.1 将各操作用阿拉伯数字表示，将可行方案拼接成一个字符串，根据字符串对应的数字大小，来确定字母排序最小的方案。

二?代码实现：

# http://www.mianshigee.com/question/16649hrq
import collections
import math

#1 注意事项：Rotation时，需要重新赋值矩阵数据，否则将前后一起变化。
#2 注意事项：用队列存储操作过程，在讲队列赋值给新队列时，需要特别注意队列中的元素顺序，因为它对应着操作顺序。
                # new_step = []
                # new_step.append(dir_i)
                # for step_i in step:
                #     new_step.append(step_i)
                # # 要保证顺序不能变，否则最终输出时，顺序将有误
                # new_step.append(dir_i) # 在尾部添加
                # # 并将头部的数据去除
                # new_step.pop(0)
#3 目标元素的确定：统计1/2/3三个元素在目标区域中的个数，以个数最大者对应的元素为目标元素，见findTarget函数
#4 一些法则：
#4.1 旋转一次之后，如果目标元素发生了变化，则return
#4.2 旋转一次之后，如果目标元素未发生变化，但数量减少，则return
#4.3 旋转一次之后，如果目标元素未发生变化，并且数量未减少，则进入下一次dfs搜索；
#5 终止条件
#5.1 目标区域中的目标元素的个数为8，成功return！
#5.1.1 保存当前方案
#5.1.2 存储当前的目标元素
#5.2 如果DFS搜索深度大于设定值，则错误return。// self.MaxDeep = 4 # 这次数据特别有效，有助于提升算法的执行速度。
#5.3 假设当前目标元素能够找到可行的方案，则不再对其他目标元素进行搜索。
#5.4 对当前目标元素的所有方案进行分析，选择长度最短、按字母顺序排序的方案。
#5.4.1 将各操作用阿拉伯数字表示，将可行方案拼接成一个字符串，根据字符串对应的数字大小，来确定字母排序最小的方案。


# 将数据转存为矩阵
def data2Matrix(subData):
    newData = [[0]*7 for i in range(7)]
    # 将subData的数据填充进入
    for i in range(24):
        if i == 0:
            newData[0][2] = subData[i]
        elif i == 1:
            newData[0][4] = subData[i]
        elif i == 2:
            newData[1][2] = subData[i]
        elif i == 3:
            newData[1][4] = subData[i]
        elif 4<=i<=10:
            newData[2][i-4] = subData[i]
        elif i ==11:
            newData[3][2] = subData[i]
        elif i == 12:
            newData[3][4] = subData[i]
        elif 13<=i<=19:
            newData[4][i-13] = subData[i]
        elif i == 20:
            newData[5][2] = subData[i]
        elif i == 21:
            newData[5][4] = subData[i]
        elif i == 22:
            newData[6][2] = subData[i]
        elif i == 23:
            newData[6][4] = subData[i]
    return newData
# 查找目标区域的元素，并排序
def findTarget(subData):
    # 统计各元素的数量
    num1 = 0
    num2 = 0
    num3 = 0
    # 给定目标区域的坐标列表
    Target_areas = [[2,2],[2,3],[2,4],[3,2],[3,4],[4,2],[4,3],[4,4]]
    # res = ''#存放数据
    for i in range(8):
        rr,cc = Target_areas[i][0],Target_areas[i][1]
        # res = res + str(newData[rr][cc])
        if subData[rr][cc] == 1:
            num1 = num1 + 1
        elif subData[rr][cc] == 2:
            num2 = num2 + 1
        elif subData[rr][cc] == 3:
            num3 = num3 + 1
    ans = [num1,num2,num3]
    min_ans = min(ans)
    max_ans = max(ans)
    targetdict = {}
    for i in range(1,4,1):
        if ans[i-1] == max_ans and 'max' not in targetdict.keys():
            targetdict['max'] = [i,max_ans] # 存档数据说明【元素值，元素数量】
        elif ans[i-1] == min_ans and 'min' not in targetdict.keys():
            targetdict['min'] = [i, min_ans]
        else:
            targetdict['mid'] = [i, ans[i-1]]
    return targetdict
# 设置旋转，并返回旋转后的矩阵和目标区域的字典
def Rotation(Data,dir):
    # 数据需要转存
    subData = []

    for i in range(len(Data)):
        temp = []
        for j in range(len(Data[0])):
            temp.append(Data[i][j])
        subData.append(temp)

    if dir == 0: #沿0方向旋转1次
        temp = subData[0][2]
        for i in range(7):
            if i == 6:
                subData[i][2] = temp
            else:
                subData[i][2] = subData[i+1][2]
    elif dir == 1: #沿1方向旋转1次
        temp = subData[0][4]
        for i in range(7):
            if i == 6:
                subData[i][4] = temp
            else:
                subData[i][4] = subData[i+1][4]
    elif dir == 2:
        temp = subData[2][6]
        for i in range(6,-1,-1):
            if i == 0:
                subData[2][0] = temp
            else:
                subData[2][i] = subData[2][i-1]
    elif dir == 3:
        temp = subData[4][6]
        for i in range(6,-1,-1):
            if i == 0:
                subData[4][0] = temp
            else:
                subData[4][i] = subData[4][i-1]
    elif dir == 4:
        temp = subData[6][4]
        for i in range(6,-1,-1):
            if i == 0:
                subData[0][4] = temp
            else:
                subData[i][4] = subData[i - 1][4]
    elif dir == 5:
        temp = subData[6][2]
        for i in range(6,-1,-1):
            if i == 0:
                subData[0][2] = temp
            else:
                subData[i][2] = subData[i - 1][2]
    elif dir == 6:
        temp = subData[4][0]
        for i in range(7):
            if i == 6:
                subData[4][6] = temp
            else:
                subData[4][i] = subData[4][i+1]
    elif dir == 7:
        temp = subData[2][0]
        for i in range(7):
            if i == 6:
                subData[2][6] = temp
            else:
                subData[2][i] = subData[2][i+1]
    ## 获得旋转后的数据，以及中间的8个目标元素
    targetdict = findTarget(subData)
    return subData,targetdict

# 寻找长度最小的方案，保存起来
def findWays(ways):
    LEN = len(ways)
    if LEN == 1:
        return ways[0]
    else:
        Init_len = math.inf
        FianlWays = []
        for i in range(LEN):
            temp = ways[i][0]
            if len(temp) < Init_len: # 确定方案的最小长度
                Init_len = len(temp)
        for i in range(LEN):# 寻找长度最小的方案
            temp = ways[i][0]
            if len(temp) == Init_len:
                FianlWays.append(ways[i])
    ## 寻找长度相同，但字母排序最小的方案
    LEN = len(FianlWays)
    if LEN==1:
        return FianlWays[0]
    else:
        len2 = len(FianlWays[0][0])
        Init_int = math.inf
        for i in range(LEN):
            temp = FianlWays[i][0]
            res = ''
            for j in range(len2):
                res = res + str(temp[j])
            if int(res) < Init_int: # 查找字母排序最小值
                Init_int = int(res)
        ## 确定字母排序最小值对应的方案
        for i in range(LEN):
            temp = FianlWays[i][0]
            res = ''
            for j in range(len2):
                res = res + str(temp[j])
            if int(res) == Init_int: # 查找字母排序最小值
                return FianlWays[i]

## 开始DFS处理
class Solutions:
    def DFS(self):
        # 设置DFS的最深深度
        self.MaxDeep = 4 # 这次数据特别有效，有助于提升算法的执行速度。
        # 查询目标区域的元素
        targetdict = findTarget(subData)
        # 存放最终结果
        self.FinalWays = []
        for candicate_i in range(3):
            ## 1 初步选定最初的目标元素（数量最多）
            if candicate_i == 0:
                label = targetdict['max'][0]
                label_num = targetdict['max'][1]
            elif candicate_i == 1:
                label = targetdict['mid'][0]
                label_num = targetdict['mid'][1]
            elif candicate_i == 2:
                label = targetdict['min'][0]
                label_num = targetdict['min'][1]
            ## 2 接下来，DFS搜索当前目标元素的所有可行方案
            self.ways = []
            for dir_i in range(8):
                step = [dir_i]
                self.dfs(subData,label,label_num,dir_i,step)
            ## 3 寻找长度最小的方案，保存起来
            if len(self.ways)>0:# 说明已经找到了合适的方案
                # 寻找长度最小的方案，保存起来
                Ways = findWays(self.ways)
                self.FinalWays.append(Ways)
                break
        # 对保存的方案进行处理
        if len(self.FinalWays)>0: # 说明具有可行方案
            # 按照输出要求进行输出。
            return findWays(self.FinalWays)
        else:
            # 说明没有可行方案
            return "No Solution"

    def dfs(self,data,label,label_num,dir,step):
        # 设置旋转，并返回旋转后的矩阵和目标区域的字典
        new_subData, new_targetdict = Rotation(data, dir)
        new_label = new_targetdict['max'][0]
        new_label_num = new_targetdict['max'][1]
        # 什么是否终止：终止1：
        if new_label == label:
            if new_label_num == 8:# 标签未发生变化，并且目标区域都是同一个元素
                self.ways.append([step,label])# 保存当前方案及label
                return
        else:
            return
        # 终止2：如果step超过了预期的深度，则报错返回
        if len(step) > self.MaxDeep:
            return
        ## 2 不满足终止条件，则继续执行
        if new_label == label and new_label_num>=label_num: # 只有当目标元素保持不变，并且数量不减小时，说明有效
            # 进行下一次dfs循环
            for dir_i in range(8):
                new_step = []
                new_step.append(dir_i)
                for step_i in step:
                    new_step.append(step_i)
                # 要保证顺序不能变，否则最终输出时，顺序将有误
                new_step.append(dir_i) # 在尾部添加
                # 并将头部的数据去除
                new_step.pop(0)
                self.dfs(new_subData,new_label,new_label_num,dir_i,new_step)
        else:
            return
        return

## 首先迎接数据，将数据存放到7*7的矩阵中
data = []
while True:
    n = input().strip()
    if len(n) == 1 and int(n)==0:
        break
    # 存入矩阵中
    temp = list(map(int,n.strip().split(' ')))
    data.append(temp)
# print(data)
# case的数量
N = len(data)
# 设置操作标志
action = {0:['A'],1:['B'],2:['C'],3:['D'],4:['E'],5:['F'],6:['G'],7:['H']}

for casei in range(N):
    subData = data[casei]
    # 将数据转化为矩阵
    subData = data2Matrix(subData)
    test = Solutions()
    ans = test.DFS()
    # 打印
    res = ''
    for i in ans[0]:
        res = res + action[i][0]
    print(res)
    print(ans[1])

输入：

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0

输出：

AC
2
DDHH
2