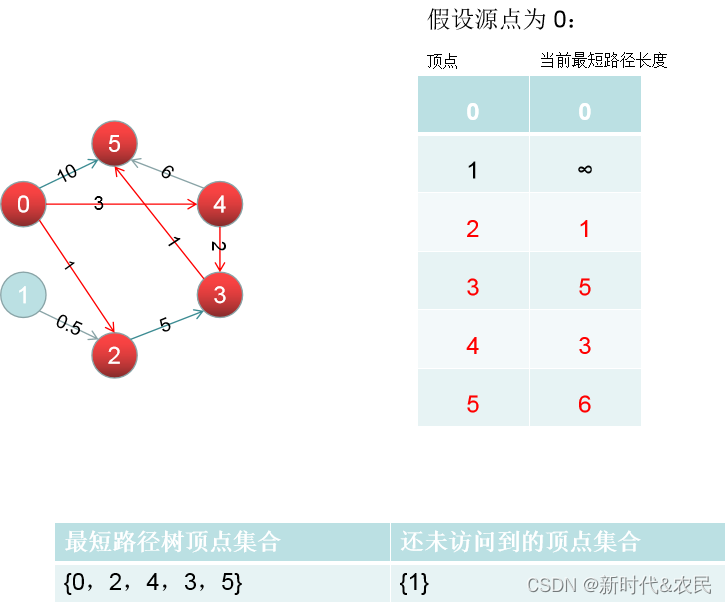
过程
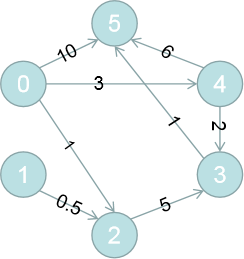
假设上图中的顶点代表各个城市,每条边的权值代表城市间的路程长度。0->5 表示可以从城市 0 直达城市 5,路程长度 10;0->2->3->5 代表可以经过城市 2,3 到达城市 5,路程长度 7。
你想要找到从城市0到城市5的最短路程,或者从城市0到其余各个城市的最短路程。这就是单源最短路径问题:给定带权图G和源点v,求从v到图G中其余各顶点的最短路径。
如何求得这些路径?迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径算法。(条件:所有边的权值为正。)
-
用一个数组D记录源点到各点的最短路径长度。假设源点为 0 (出发点),则D[3]表示从点0到点3的当前的最短路径长度。
-
数组D的初始状态:源点0到自身的距离为0,D[0]= 0;若源点0到其余顶点i有边,则D[i]为边的权值;否则D[i]为∞,表示没有直达路径;上图初始状态:
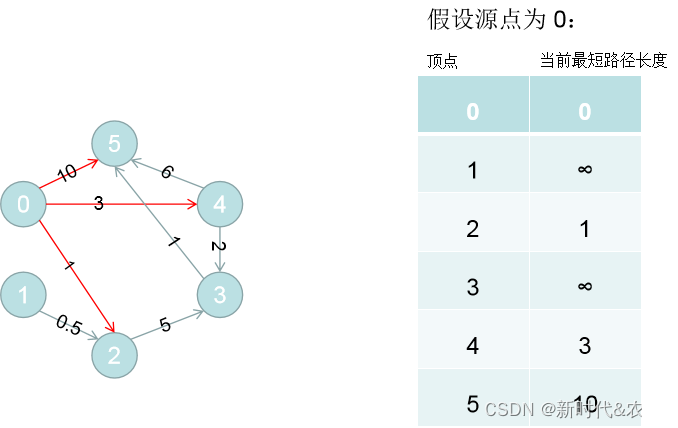
3.类似Prim算法,我们需要两个集合,一个集合包含最短路径树的顶点,另一个集合是还没加入到最短路径树的顶点。此上图中,

此时我们如果找到没有访问的顶点集合中,能够以最短方式抵达的那个顶点,在例子中为顶点2,权值为1,那就说从源点0到顶点2,它的最短路径就是1。 -
确定新的顶点的最短路径后,将顶点2加入最短路径树的集合,再看顶点2的所有邻边。只有一条邻边2->3,权值为5;因为D[3] = ∞,表示源点0到顶点3没有路径,此时通过边2->3,有了从源点0到3 的路径:0->2->3,权值为1+5 = 6 ,比我们现在要存的D[3] = ∞ 要短,所以在数组D[3]中要更新记录更小的路径长度:D[3]= 1+5 = 6;
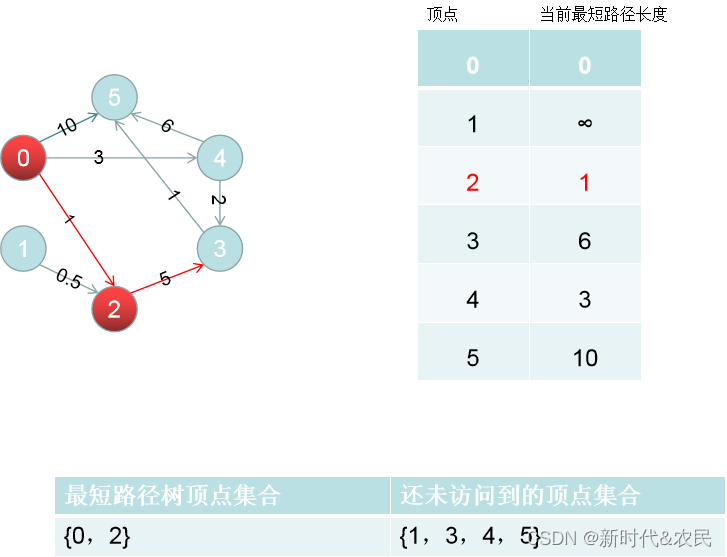
-
此时从还没有知道最短路径的这些顶点中,现在存的那个最短路径能抵达的顶点是谁,上图中是D[4] = 3,也就是顶点4,找到的这条路径就是从 0 到 4 的最短路径。因为到其他的节点所需要的路程更长,若以这些节点为中转点,再返回到顶点4的话,将会花费更多的路程。找到最短路径后,将顶点加入最短路径树的集合中。
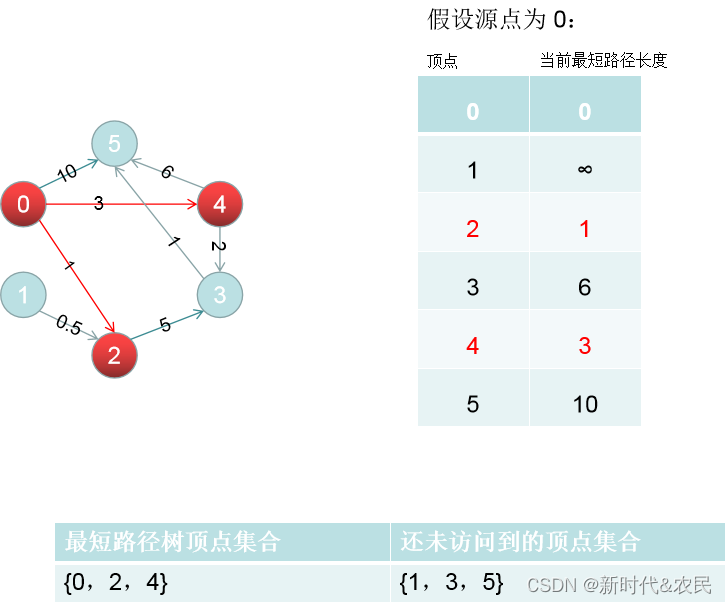
-
访问新加入的顶点4的邻边,看是否能以顶点4作为中转到达其他顶点的路径是否更短一些;
邻边4->3:由于0->3,D[3] = 6,而4->3的路径长度为2,从0->4->3 就找到以了一条权值为 3+2 = 5 的路径,比现存的D[3] = 6要小,就可以更新数组D[3]的值为5;之前的0->2->3就可以要了。
邻边4->5:由于0->5,D[5] = 10,而4->5的路径长度为6,从0->4->5 就找到了一条权值为 3+6= 9 的路径,比现存的D[5]= 10 要小,更新数组D[5] = 0;
重复步骤4,找出现在存的那个最短路径能抵达的顶点是谁,上图中是D[3] = 6。
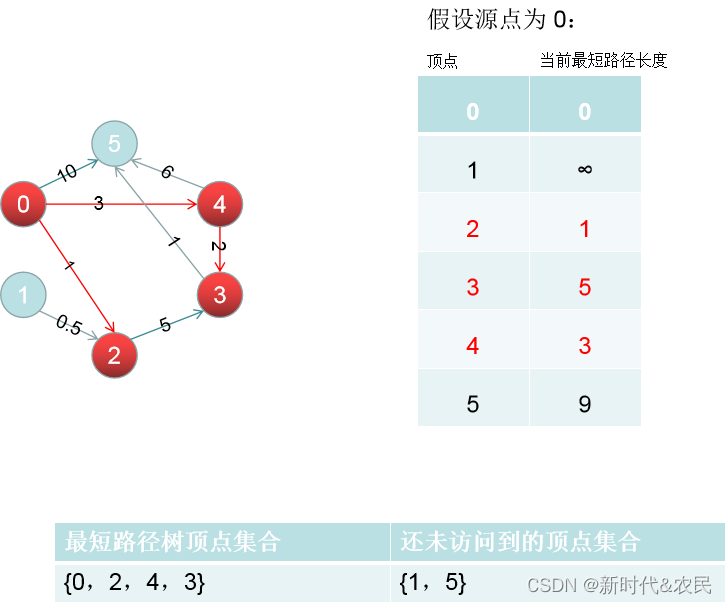
-
访问顶点3的邻边,重复上述过程。