[数据结构与算法]【数据结构与算法】图解线性表1

图解数据结构与算法之线性表

一，说明

数据结构时计算机的一门基础课程，在用计算机解决问题时，通常不是用来进行数值的计算，而是把实际的问题抽象成一个数据模型来解决问题。(比如表，图，树等数据结构)

二，线性表的定义

定义：零个或者多个数据元素的有限序列
注意：有序性和有限性
相关概念：前一个元素是后一个元素的直接前驱元素，后一个元素是前一个元素的直接后继元素，第一个元素没有直接前驱元素，最后一个元素没有直接后继元素。

在较为复杂的线性表中，一个元素可以由多个数据项组成。

三，线性表的顺序存储结构

1.定义

1.1顺序存储的定义

定义：用一段地址连续的存储单元一次存储线性表的数据元素。

如图：

1.2顺序存储方式

当数据元素的数据类型相同时，可以用一维数组来实现顺序存储结构。
最大储存容量：数组的长度就是这个线性表的最大存储容量。
当前长度：线性表中当前的元素个数就是线性表的当前长度。

线性表的当前长度不能比最大储存容量大。

#define MAXSIZE 20
typedef int ElemType;
typedef struct{
    ElemType date[MAXSIZE];
    int length;
}SqList;

1.3数据长度与线性表长度的关系

• 数组长度是存储线性表的存储空间的长度，存储分配后这个量一般是不会变化的。
• 线性表的长度是线性表中元素的个数，随着线性表中元素的插入删除而改变。
• 线性表的长度永远小于等于数组的长度。

1.4地址的计算方法

• 用数组存储顺序线性表。
• 在线性表中和数组不同的是，线性表的定义是从1开始的。而在数组中下标是从0开始的。
• 存储器中的每个存储单元都有编号，这个编号称为地址。
• 线性表中第i+1个元素的存储位置和第i个元素的存储位置满足：
  LOC(a[i+1])=a[i]+c；
  其中c是每个元素所占的内存空间。

2.顺序存储结构的插入删除

2.1获取元素操作

要想获取顺序线性表的第i个元素的值，只要i在数组下标数值的范围内，只需要返回数组的第i-1的值。
参考示例：

int GetElem(sqList L,int i,int *e){
    if(L.length==0||i<1||i>L.length){
        return 0;
    }
    else{
        *e=L.dete[i-1];
    }
}

2.2插入元素

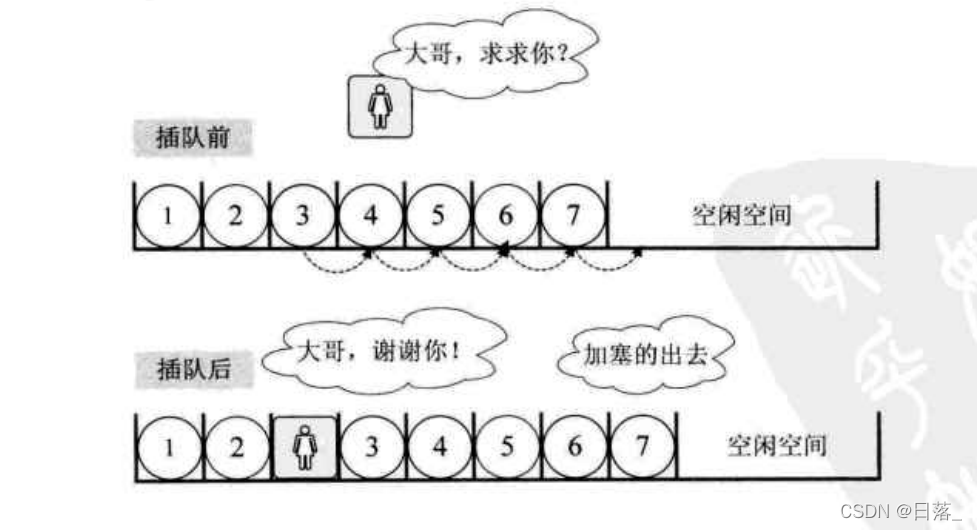
算法思路：

1. 如果插入位置不合理，抛出异常。
2. 如果线性表的长度大于等于数组长度，抛出异常。
3. 从最后一个元素遍历到第i个元素，分别把他们向后移动一个位置。
4. 将要插入的元素插入到位置i处。
5. 表长加1。

参考示例：

int ListInsert(Sqlist *L,int i,int e){
    int k;
    if(L->length=MAXSIZE){
        return 0;
    }
    if(i<1||i>L->length+1){
        return 0;
    }
    if(i<=L->length){
        for(k=L->length;k>=i-1;k--){
            L->date[k+1]=L->date[k];
        }
        L->date[i-1]=e;
        L->length++;
        return 0;
    }
}

2.3删除元素

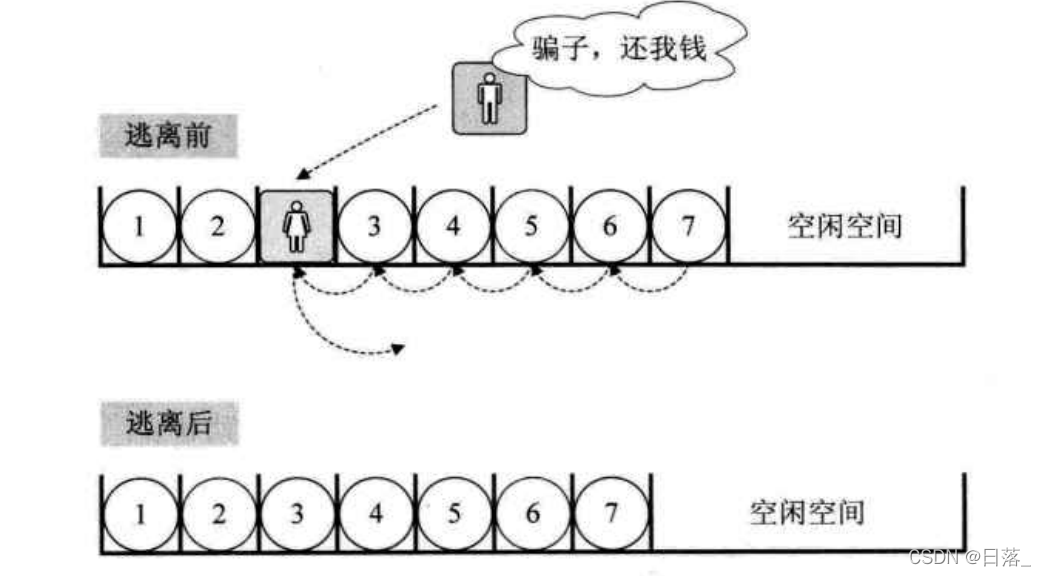
算法思路：

1. 如果删除位置不合理，抛出异常。
2. 取出删除元素。
3. 从删除元素的位置开始遍历到最后一个元素位置，分别将他们向前移动一个位置。
4. 表长减一。
   参考案例：

//条件：顺序线性表L已经存在，删除第i个位置的值，并返回i位置的值。
int ListDelete(Sqlist *L,int i,int e){
    int k;
    if(L->length==0){
        return 0;
    }//线性表为空
    if(i<1||i>L->length+1){
        return 0;
    }//删除位置不正确
    *e=L->date[i-1];
    if(i<L->length){//如果删除不是最后的元素
        for(k=i;k<L->length;k++){
            L->date[k-1]=L->date[k];//前移
        }

        L->length--;
        return 0;
    }
}

2.4顺序存储的优缺点

三，线性表的链式存储结构

1，单链表的读取

线性表的顺序存储结构中，我们可以很方便的计算任意一个元素的存储位置，但是在单链表中，由于要操作的元素不知到在哪个位置，所以需要从头开始找，所以在算法上，要找到相应的元素是比较麻烦的。

那么，要怎样找到单链表的第i个元素呢？
在单链表中要找到第i个元素，用遍历的思想。

1. 声明一个指针指向链表的第一个结点，初始化j=1；
2. 当j<i时，遍历整个链表，j+1；
3. 若到链表末尾第指针为空，则说明第i个结点不存在；
4. 否则查找成功，返回结点p的数据；

2，单链表的插入与删除

2.1单链表的插入

假设往单链表的第i个位置插入新的结点s，即插入到p和p->next之间，实现三者逻辑关系的变化。

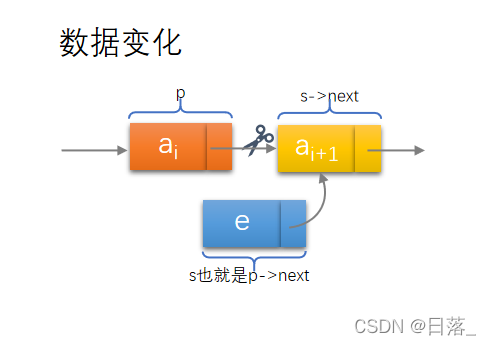
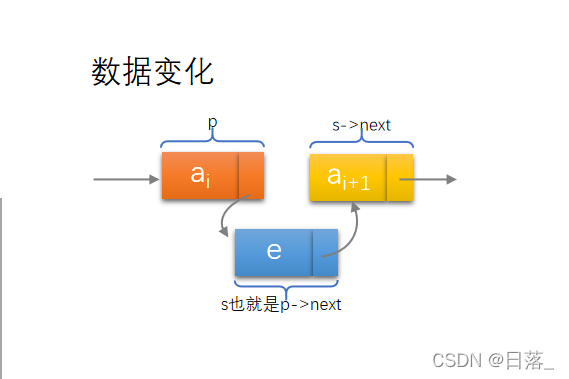
实现方法：

s->next=p->next;//将p的后继结点赋值给s的后继结点
p->next=s;//将s赋值给p的后继结点

将数据插入到表头和表尾时，方法仍然适用。

算法实现：

1. 声明一个指针p指向表头结点，初始化j=1；
2. 当j<i时，遍历整个链表，j+1；
3. 若到链表末尾第指针为空，则说明第i个结点不存在；
4. 否则查找成功，手动开辟内存空间生成空结点s；
5. 将数据元素赋值给s->date;
6. 返回成功；
   

2.1单链表的删除

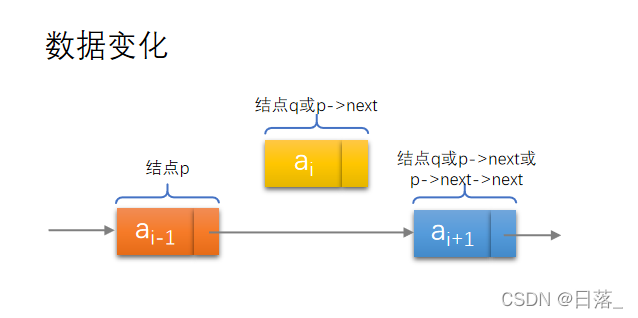
设储存a的结点时q，要实现q节点的删除，其实就是绕过前驱结点的指针，指向它的后继结点。

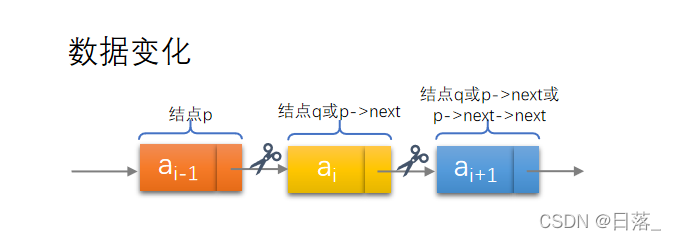
实现方法：

q=p->next;
p->next=q->next;//将q的后继元素赋值给p的后继元素

算法实现：

1. 声明一个指针p指向表头结点，初始化j=1；
2. 当j<i时，遍历整个链表，j+1；
3. 若到链表末尾第指针为空，则说明第i个结点不存在；
4. 否则查找成功，将想要删除的结点p->next赋值给q；
5. 单链表删除的标准语句：p->next=q->next；
6. 将结点q的数据赋值给e并返回；
7. 释放结点q；
   

3，单链表的整表创建

创建单链表的过程就是一个动态生成链表的过程，依次 建立个元素的结点，并插入链表。
创建单链表的过程可以分为头插法和尾插法。

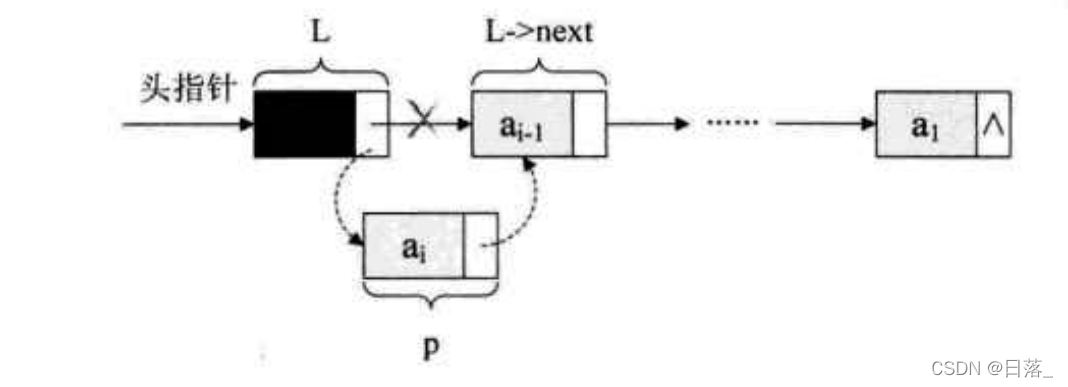
算法思路：

1. 声明一个指针p和一个计数器比变量i；
2. 声明初始化一个空链表L；
3. 让L的头结点指针指向NULL，即初始化一个带有头结点的空指针；
4. 生成一个新的结点赋值给p；
5. 将p结点插入到头结点与前一新结点之前；

把数据插入到头结点与前一新结点之前的方法叫做头插法。
按照排队的思想，新的结点插入到链表的末尾的方法叫做尾插法。

4，单链表的整表删除

当我们不再使用单链表时，需要对创建的单链表进行销毁。释放内存，方便其他程序的使用。

算法思路：

1. 声明指针p和q；
2. 将第一个结点赋值给p；
3. 循环：

• 将下一结点赋值给q；
• 释放p；
• 将q赋值给p；

四，单链表结构与顺序存储结构的优缺点

• 若线性表的查找频繁，很少进行插入和删除操作时，通常使用顺序存储结构。
• 若线性表中元素个数比较大或者经常进行频繁的插入和删除操作时，通常使用链式存储结构。

【数据结构与算法】图解线性表2

下文图解静态链表循环链表以及双向链表。

五，静态链表

六，循环链表

七，双向链表

八，总结