[数据结构与算法]十大算法及其典型问题实践

ps: 十大算法合集，学习来源是尚硅谷Java数据结构与java算法，自留复习。

1.二分法查找算法非递归实现

 int binarySearch(int[] arr, int target) {

      int left = 0;
      int right = arr.length - 1;
      while (left <= right) {
          int mid = (left + right) / 2;

          if (arr[mid] > target) {
              right = mid - 1;
          } else if (arr[mid] < target) {
              left = mid + 1;
          } else {
              return mid;
          }
      }
      return -1;
    }

2.分治算法和汉诺塔问题

void hanoTower(int num, char a, char b, char c) {
    if (num == 1) {
        //如果只有一个盘
        System.out.println("第1个盘从" + a + "->" + c);
    } else {
        //如果两个盘以上 看做下面一个盘和上面所有盘
        //先把上面的盘a->b 移动过程会使用到c
        hanoTower(num - 1, a, c, b);
        //把最下面的盘a->c
        System.out.println("第" + num + "个盘从" + a + "->" + c);
        //把b所有的盘b->c 移动过程会使用到a
        hanoTower(num - 1, b, a, c);
    }
}

3.动态规划算法和背包问题

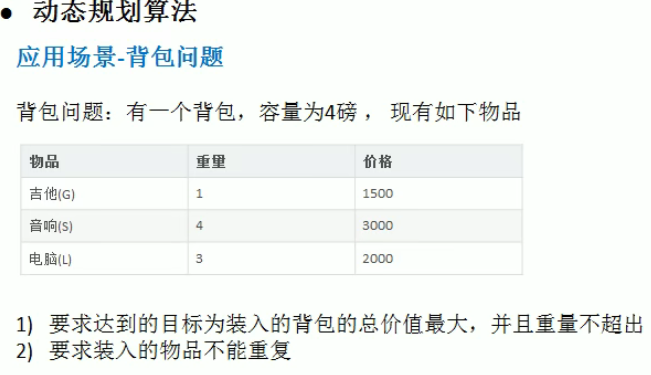
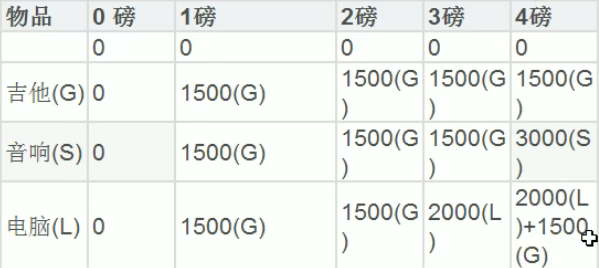
算法实现

int[] w = {1, 4, 3};//物品重量
int[] value = {1500, 3000, 2000};
int m = 4;//背包容量
int n = value.length;//物品个数
//v[i][j]表示前i个物品中能装入容量为j的背包中的最大值
// 行标题是背包容量0 1 2 3 4  列标题是物品0 1500 3000 2000
int[][] v = new int[n + 1][m + 1];
//用来记录选择的搭配
int[][] path = new int[n + 1][m + 1];
//初始化 第一列 和 第一行
for (int i = 0; i < v.length; i++) {
    v[i][0] = 0;
}
for (int i = 0; i < v[0].length; i++) {
    v[0][i] = 0;
}

重点

//根据公式进行动态规划处理 不处理第一行及第一列
for (int i = 1; i < v.length; i++) {
    for (int j = 1; j < v[0].length; j++) {
        if (w[i - 1] > j) {     //如果要加入的商品容量>背包容量  w[0]开始
            v[i][j] = v[i - 1][j];     //采用上一格的装配策略
        } else {   //如果要加入的商品容量<背包容量
            //                               value,w从0开始
            //v[i][j] = Math.max(v[i - 1][j], value[i-1] + v[i - 1][j - w[i-1]]);
            if (v[i - 1][j] < value[i - 1] + v[i - 1][j - w[i - 1]]) {
                v[i][j] = value[i - 1] + v[i - 1][j - w[i - 1]];
                //把当前情况记录到path
                path[i][j] = 1;
            } else {
                v[i][j] = v[i - 1][j];
            }
        }
    }
}

//遍历输出v[i][j]
for (int i = 0; i < v.length; i++) {
    for (int j = 0; j < v[0].length; j++) {
        System.out.print(v[i][j] + " ");
    }
    System.out.println();
}
//输出path
for (int i = 0; i < path.length; i++) {
    for (int j = 0; j < path[i].length; j++) {
        if(path[i][j]==1) {
            System.out.print("第" + i + "个商品放入到背包中" + " ");
        }else{
            System.out.print(" * ");
        }
    }
    System.out.println();
}
//逆向遍历
int i = path.length - 1;
int j = path[0].length - 1;
while (i > 0 && j > 0) {
    if (path[i][j] == 1) {
        System.out.print("第" + i + "个商品放入到背包中" + " ");
        j -= w[i - 1];  //第i个商品的重量w[i - 1]
    }
    i--;
}

输出结果

4.KMP算法和字符匹配问题

暴力匹配

//暴力匹配算法  一个个字符依次去比较
![在这里插入图片描述](https://img-blog.csdnimg.cn/6e6170e154074462bfe8edbe08db945c.png)

static int violenceMatch(String str1, String str2) {
    char[] s1 = str1.toCharArray();
    char[] s2 = str2.toCharArray();
    int l1 = s1.length;
    int l2 = s2.length;
    int i = 0;//指向s1索引
    int j = 0;//指向s2索引
    while (i < l1 && j < l2) {//匹配时不可越界
        if (s1[i] == s2[j]) {
            i++;
            j++;
        } else {
            j = 0;
            i = i - (j - 1);//i匹配前的位置向后移动一位  重新开始匹配
        }
    }
    //判断是否匹配成功  返回匹配起始位置
    if (j == l2) {
        return i - j;
    }
    return -1;
}

kmp算法（这里参考的方法来源是KMP算法
首先需要建立所要匹配字符的前缀表

static void prefixTable(char[] string, int[] prefix, int n) 
    prefix[0] = 0;
    int len = 0;
    int i = 1;
    while (i < n) {
        if (string[i] == string[len]) {
            len++;
            prefix[i] = len;
            i++;
        } else {
            if (len > 0) {
                len = prefix[len - 1];
            } else {
                prefix[i] = len;
                i++;
            }
        } 
    }
    //移动prefix 所有数据后移一位 舍弃最后一位 第一位补-1
    for (int k = n - 1; k > 0; k--) {
        prefix[k] = prefix[k - 1];
    }
    prefix[0] = -1;
    //print
    System.out.print("前缀表 ");
    for (int p : prefix) {
        System.out.print(p + " ");
    }
    System.out.println();
}

利用前缀表进行查找 加快速度

static void kms_search(String str1, String str2) {
    char[] text = str1.toCharArray();
    char[] pattern = str2.toCharArray();
    int[] prefix = new int[str2.length()];
    prefixTable(pattern, prefix, prefix.length);
    //text[i]     len[text] = m
    //pattern[j]  len[pattern] = n
    int i = 0, j = 0;        //两下标
    int m = text.length;     //查找范围长度
    int n = pattern.length;  //要查找的字符串长度
    while (i < m) {
        if (j == n - 1 && text[i] == pattern[j]) {
            System.out.println("找到位置在 " + (i - j));
            j = prefix[j];   //继续找下一个匹配的位置(可能有多个匹配位置)
        }
        if (text[i] == pattern[j]) {
            i++;
            j++;
        } else {
            j = prefix[j];
            if (j == -1) {  //下标指到了前缀表第一位,值为-1   就自动指向下一位再比较
                j++;
                i++;
            }
        }
    }
}

5.贪心算法和集合覆盖问题

贪心算法结果不一定是最优（有可能最优解）


主要算法实现

//广播电台  存放每一个电台及其对应的覆盖地区String集
  HashMap<String, HashSet<String>> broadcasts = new HashMap<>();
//所有地区集合(k1,k2...)  在选择过程中不断减少
  HashSet<String> allAreas = new HashSet<>();
//存放已选择的电台的集合
  ArrayList<String> selects = new ArrayList<>();
//定义一个临时的集合  在遍历的过程中,存放每个电台(k1,k2...)覆盖地区和未覆盖地区allAreas的交集
  HashSet<String> tempSet = new HashSet<>();
//定义maxKey 在每次遍历过程中,为能够覆盖最多未覆盖地区的电台的key(k1,k2...)
  String maxKey = null;
//直到所有地区都被覆盖停止循环
  while (allAreas.size() != 0) {
    //每while循环一次 置空maxKey
      maxKey = null;
    //遍历广播电台
      for (String key : broadcasts.keySet()) {
        //每次循环清空tempSet
          tempSet.clear();
          HashSet<String> area = broadcasts.get(key);
          tempSet.addAll(area);
          tempSet.retainAll(allAreas);//求出交集并直接赋给了tempSet
        //找到maxKey
          if (tempSet.size() > 0 &&         /*这里是贪心算法的特点所在，即每次选取最优的*/
                (maxKey == null || tempSet.size() > broadcasts.get(maxKey).size())) {
            maxKey = key;
          }
      }
    //找到了maxKey,加入selects里,从allAreas剔除已加入的地区
      if (maxKey != null) {
          allAreas.removeAll(broadcasts.get(maxKey));
          selects.add(maxKey);
      }
  }
  System.out.println("结果 "+selects.toString());

6.普利姆算法(Prim)和修路问题

定义一个图结构类

class MGraph {
    int verx;//图的节点个数
    char[] data;//节点数据
    int[][] weight;//存放边(边上权值),即邻接矩阵
    public MGraph(int verx) {
        this.verx = verx;
        data = new char[verx];
        weight = new int[verx][verx];
    }
}

邻接矩阵举例

 //10000表示两点之间不连通
 int[][] weight = {
        {10000, 5, 7, 10000, 10000, 10000, 2},
        {5, 10000, 10000, 9, 10000, 10000, 3},
        {7, 10000, 10000, 10000, 8, 10000, 10000},
        {10000, 9, 10000, 10000, 10000, 4, 10000},
        {10000, 10000, 8, 10000, 10000, 5, 4},
        {10000, 10000, 10000, 4, 5, 10000, 6},
        {2, 3, 10000, 10000, 4, 6, 10000}
 };

prim算法实现

 /**
     * @param graph 图对象
     * @param v     表示从第几个顶点开始生成
     */
    void prim(MGraph graph, int v) {
        //标记已经访问的节点为1  数组已经自动初始化都为0了无需手动初始化
        int[] visited = new int[graph.verx];
        //标记起始节点为已访问
        visited[v] = 1;
        int minWeight = 10000;//要找的最小边值,这里设置为最大然后后面去循环比较获取最小边
        //记录最小边的两个顶点的下标,初始化为-1
        int h1 = -1, h2 = -1;
        //若有k个节点，prim算法过后会有k-1条边,所以这里k从1开始
        for (int k = 1; k < graph.verx; k++) {
        
            //从已经访问的节点开始延伸，看每个节点和哪个节点距离最近
            for (int i = 0; i < graph.verx; i++) {
                //找到顶点i相连的边最小的顶点
                for (int j = 0; j < graph.verx; j++) {

                    if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
                        minWeight = graph.weight[i][j];
                        h1 = i;
                        h2 = j;
                    }
                }
            }
            //找到最小边
            System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值=" + minWeight);
            //将找到的最小边连接的节点标记为已访问
            visited[h2] = 1;
            //找下一条最小边前将此置为最大值，即重置
            minWeight = 10000;
        }
    }

7.克鲁斯卡尔算法(Kruskal)和公交车站问题

算法实现
1.定义边结构类

class Edge {
    char start;    //起点
    char end;     //终点
    int weight;   //边(权值)
    public Edge(char start, char end, int weight) {
        this.start = start;
        this.end = end;
        this.weight = weight;
    }
}

2.定义顶点数组和邻接矩阵

 char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
 //使用INF表示两个顶点不能连通
 private static final int INF = Integer.MAX_VALUE;
 int[][] matrix = {
        //      A     B    C    D    E    F    G     
        //此处有用数据为12个 即有效边为12条
              {0, 12, INF, INF, INF, 16, 14},
              {12, 0, 10, INF, INF, 7, INF},
              {INF, 10, 0, 3, 5, 6, INF},
              {INF, INF, 3, 0, 4, INF, INF},
              {INF, INF, 5, 4, 0, 2, 8},
              {16, 7, 6, INF, 2, 0, 9},
              {14, INF, INF, INF, 8, 9, 0},
        };

3.根据顶点数组和邻接矩阵创建kruskal类
获取以下信息

  static int edgeNum;//有效边数目
  char[] vertex;//顶点数组
  private int[][] matrix;//邻接矩阵

4.构造所有边

Edge[] getEdges() {
       int len = vertex.length;
       Edge[] edges = new Edge[edgeNum];
       int k = 0;
       for (int i = 0; i < len; i++) {
           for (int j = i + 1; j < len; j++) {
               if (this.matrix[i][j] != INF) {
                   Edge edge = new Edge(vertex[i], vertex[j], matrix[i][j]);
                   edges[k++] = edge;
               }
           }
       }
       return edges;
}

5.对边进行排序

private void sortEdge(Edge[] data) {
    //冒泡排序  从小到大排列
    for (int i = 0; i < data.length - 1; i++) {
        for (int j = 0; j < data.length - 1 - i; j++) {
            if (data[j].weight > data[j + 1].weight) {
                Edge temp = data[j];
                data[j] = data[j + 1];
                data[j + 1] = temp;
            }
        }
    }
 }

6.定义两个所需方法

 /**
  * @param ends 记录了各个顶点对应的终点的数组,是在遍历过程中逐步形成的
  * @param i    顶点下标
  * @return     顶点终点下标
  */
 //获取下标为i的顶点的终点,用于判断两个顶点的终点是否相同
 int getEnd(int[] ends, int i) {
     while (ends[i] != 0) {
         i = ends[i];
     }
     return i;
 }
 //根据顶点值获取下标（A-0,B-1,...)
 int getPos(char c) {
     for (int i = 0; i < vertex.length; i++) {
         if (vertex[i] == c) {
             return i;
         }
     }
     return -1;
 }

7.算法主体实现

void kruskal() {
    int[] ends = new int[edgeNum];//终点数组
    int index = 0;//结果数据的索引
    //结果数组  存放每次加入的边
    Edge[] res = new Edge[edgeNum];
    //所有有效边
    Edge[] edges = getEdges();
    sortEdge(edges);//边按权值从小到大排列
    System.out.println("排序后：" + Arrays.toString(edges));
    //遍历每条边 若不构成回路,就加入结果数组,即添加到最小生成树
    for (int i = 0; i < edgeNum; i++) {
        int p1 = getPos(edges[i].start);
        int p2 = getPos(edges[i].end);
        int m = getEnd(ends, p1);
        int n = getEnd(ends, p2);
        if (m != n) {//如果没有构成回路
            ends[m] = n;//设置m在已有最小生成树中的终点为n
            res[index++] = edges[i];//将边加入最小生成树
        }
    }
    //打印结果
    System.out.println("最小生成树：" + Arrays.toString(res));
}

8.迪杰斯特拉算法(Dijkstral)和最短路径问题

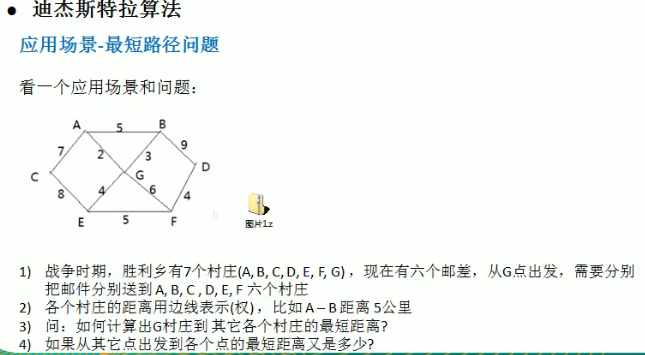
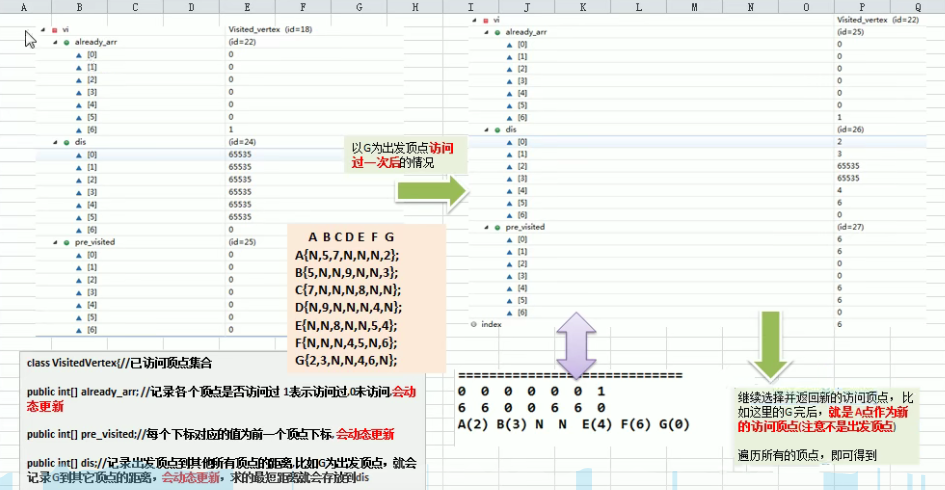
过程分析
自己画的图解

具体代码
新建两个类

//已访问顶点集合
class VisitedVertex {
    //记录各个顶点是否访问过,0=未访问,1=已访问,会动态更新
    private int[] already_arr;
    //各个顶点的前一个顶点下标,会动态更新
    private int[] pre_visited;
    //记录出发顶点到所有顶点的距离,会动态更新,求得的最短距离就会存放到dis里
    private int[] dis;

    //构造器                顶点个数    出发顶点下标
    public VisitedVertex(int length, int index) {
        this.already_arr = new int[length];
        this.pre_visited = new int[length];
        this.dis = new int[length];
        this.already_arr[index] = 1;  //将出发顶点设为已访问
        //初始化dis数组
        Arrays.fill(dis, 65535);
        this.dis[index] = 0;  //设置出发顶点到自己的距离为0
    }

    //判断顶点是否被访问过
    boolean in(int index) {
        return already_arr[index] == 1;
    }

    //获取出发顶点到index顶点的距离
    int getDis(int index) {
        return dis[index];
    }

    //更新出发顶点到index顶点的距离
    void updateDis(int index, int len) {
        dis[index] = len;
    }

    //更新pre顶点的前驱节点为index
    void updatePre(int pre, int index) {
        pre_visited[pre] = index;
    }

    //继续更新并返回新的访问顶点(不是出发顶点)
    //找到G连接的最短的距离的作为下一个访问点,比如这里G过后到A
    int updateArr() {
        int min = 65535;
        int index = 0;
        for (int i = 0; i < already_arr.length; i++) {
            if (already_arr[i] == 0 && dis[i] < min) {
                min = dis[i];
                index = i;
            }
        }
        //更新index顶点被访问
        already_arr[index] = 1;
        return index;
    }

    //显示最后结果
    void show(){
        //输出already_arr
        for (int i : already_arr) {
            System.out.print(i+" ");
        }
        System.out.println();
        for (int i : pre_visited) {
            System.out.print(i+" ");
        }
        System.out.println();
        for (int i : dis) {
            System.out.print(i+" ");
        }
    }
}

class Graph {

    private char[] vertex;//顶点数组
    private int[][] matrix;//邻接矩阵
    private VisitedVertex vv;

    public Graph(char[] vertex, int[][] matrix) {
        this.vertex = vertex;
        this.matrix = matrix;
    }
    
    /**
     * 算法实现
     * @param index 出发顶点下标
     */
    void dsj(int index) {
        vv = new VisitedVertex(vertex.length, index);
        update(index);

        for (int i = 0; i < vertex.length; i++) {
            index = vv.updateArr();//选择并返回新的访问顶点
            update(index);
        }

        //展示结果
        vv.show();
    }

    //更新index顶点到周围顶点的距离+更新周围顶点的前驱顶点
    void update(int index) {
        int len = 0;
        //遍历邻接矩阵
        for (int i = 0; i < matrix[index].length; i++) {
            //出发顶点到index顶点的距离+index顶点到i顶点的距离
            len = vv.getDis(index) + matrix[index][i];
            //如果顶点i没有被访问过,且len小于出发顶点到i顶点的距离,就更新dis
            if (!vv.in(i) && len < vv.getDis(i)) {
                vv.updateDis(i, len);//更新出发顶点到i顶点的距离
                vv.updatePre(i, index);//更新i顶点的前驱
            }
        }

    }
}

9.弗洛伊德算法(Floyd)和最短路径问题

过程分析

时间复杂度比较高n^3 三层循环

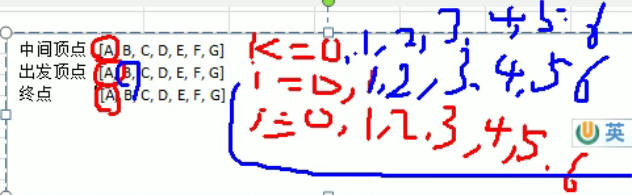
算法实现
定义一个图结构

class Graphic {
    char[] vertex;//顶点数组
    int[][] dis;//各点之前的最短距离
    int[][] pre;//各点到达目标顶点的前驱顶点

    public Graphic(char[] vertex, int[][] matrix, int length) {
        this.vertex = vertex;
        this.dis = matrix;
        this.pre = new int[length][length];
        //初始化pre 各点到达目标顶点的前驱节点为自身
        for (int i = 0; i < pre.length; i++) {
            Arrays.fill(pre[i], i);
        }
    }
//算法主体
    void floyd() {
        int len = 0;//距离
        //对中间顶点遍历,设其下标为k
        for (int k = 0; k < dis.length; k++) {
            //从顶点i开始出发   A B C D E F G
            for (int i = 0; i < dis.length; i++) {
                //到达顶点j    A B C D E F G
                for (int j = 0; j < dis.length; j++) {
                    len = dis[i][k] + dis[k][j];//从i出发经过中间顶点k到j的距离
                    if (len < dis[i][j]) {
                        dis[i][j] = len;//更新距离
                        pre[i][j] = pre[k][j];//更新前驱节点
                    }
                }
            }
        }

    }
//显示结果
    void show() {
        for (int i = 0; i < dis.length; i++) {
            for (int j = 0; j < dis[i].length; j++) {
                System.out.print(dis[i][j] + " ");
            }
            System.out.println();
        }
        System.out.println();
        for (int i = 0; i < pre.length; i++) {
            for (int j = 0; j < pre[i].length; j++) {
                System.out.print(pre[i][j] + " ");
            }
            System.out.println();
        }
    }

}

10.骑士周游回溯算法和马踏棋盘问题

算法实现

1.一些参数定义

//棋盘行列数
static int X, Y;
//创建一个数组,标记棋盘的各个位置是否被访问过
static boolean[] visited;
//step表示目前走的是第几步
static int step = 1;

2.获取下一个能走的位置集合

//根据当前位置Point,计算马还能走哪些位置Point并放入一个集合ArrayList中,最多有8个位置
static ArrayList<Point> next(Point current) {
    ArrayList<Point> list = new ArrayList<>();
    //判断马能走的八个位置
    Point p = new Point();
    if ((p.x = current.x - 2) >= 0 && (p.y = current.y - 1) >= 0) {
        list.add(new Point(p));
    }
    if ((p.x = current.x - 1) >= 0 && (p.y = current.y - 2) >= 0) {
        list.add(new Point(p));
    }
    if ((p.x = current.x + 1) < X && (p.y = current.y - 2) >= 0) {
        list.add(new Point(p));
    }
    if ((p.x = current.x + 2) < X && (p.y = current.y - 1) >= 0) {
        list.add(new Point(p));
    }
    if ((p.x = current.x - 2) >= 0 && (p.y = current.y + 1) < Y) {
        list.add(new Point(p));
    }
    if ((p.x = current.x - 1) >= 0 && (p.y = current.y + 2) < Y) {
        list.add(new Point(p));
    }
    if ((p.x = current.x + 1) < X && (p.y = current.y + 2) < Y) {
        list.add(new Point(p));
    }
    if ((p.x = current.x + 2) < X && (p.y = current.y + 1) < Y) {
        list.add(new Point(p));
    }
    return list;
}

3.算法主体部分

//棋盘 + 马的位置行列
static void traversalChess(int[][] chess, int row, int column) {
    //标记第几步
    chess[row][column] = step;
    //标记已访问
    visited[row * X + column] = true;
    //获取下一个可以走的位置集合
    ArrayList<Point> list = next(new Point(column, row));
    while (!list.isEmpty()) {
        //取出下一个可以走的位置 判断是否访问过
        Point p = list.remove(0);
        if (!visited[p.y * X + p.x]) {  //如果该位置未访问过
            step++;
            traversalChess(chess, p.y, p.x);
        }
    }
    //判断马是否完成所有走动 若没有就需要将棋盘置为0
    //step < X * Y 两种情况：1.棋盘还没走完 2.棋盘处于回溯过程
    if (step < X * Y ) {
        chess[row][column] = 0;
        visited[row * X + column] = false;
    }

最后测试下打印结果如下

X = 8;
Y = 8;
int row = 1;
int col = 1;
int[][] chess = new int[X][Y];
visited = new boolean[X * Y];
long start = System.currentTimeMillis();
traversalChess(chess, row - 1, col - 1);
long end = System.currentTimeMillis();
System.out.println("用时：" + (end - start) + "毫秒");
//打印结果
for (int i = 0; i < chess.length; i++) {
    for (int j = 0; j < chess[i].length; j++) {
        System.out.print(chess[i][j] + " ");
    }
    System.out.println();
}

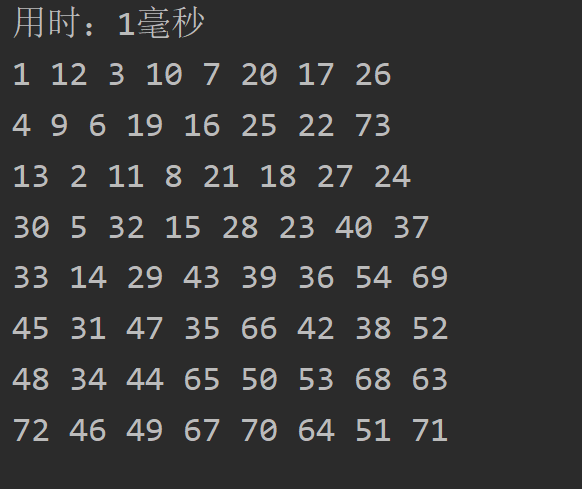
用贪心算法优化

把获得的ArrayList按从小到大排序