前言

之前呢，在介绍矩阵的博客中写到了线性方程组的求解，今天主要学习到了非线性方程组的几种解法，来记录一下

一、线性方程组求解

首先呢，回顾一下线性方程组的求解
例如，求解下列方程组的解：
在这里插入图片描述
我们学习了矩阵运算之后，会明白 x=A \ b 即为线性方程组 A*x = b 的解，因此，书写代码也很容易

A=[2 2 -1 1;4 3 -1 2;8 3 -3 4;3 3 -2 -2];
b=[4 6 12 6]';
x=A\b　%等价于 x=inv(A)*b

二、非线性方程组的几种解法

接下来呢，是今天的主角，关于非线性方程组的几种求解方法
首先呢，先介绍一下非线性方程组的形式

f(x)=0
代数方程： f(x)=a0 + a1 x+……+an x^n （an ~= 0）
超越方程：f(x)中含三角函数、指数函数、或其他超越函数。

一般稍微复杂的3次以上的代数方程或超越方程,很难甚至无法求得精确解，所以呢，我们大多求得都是方程组的近似根

1.二分法

二分法的基本原理，是数学中的零点定理：
设f(x)是区间[a,b]上的连续函数，并且f(a)f(b)<0，则存在 $\xi$ $\in$ (a, b)使得 f ( $\xi$ ) = 0。

二分法求根的基本思想：首先确定有根区间，将区间二等分，通过判断f(x)的符号，逐步将有根区间缩小，直至有根区间足够地小，便可求出满足精度要求的近似根

设方程f(x)=0在区间[a,b]内有根,二分法就是逐步收缩有根区间，最后得出所求的根。算法步骤如下：
1.输入a,b,ε的值
2. 计算f(a), f(b)
3. 如果f(a)f(b)≤0 ,则说明[a,b]是有根区间，反复执行如下操作：
a) 计算区间中点m=(a+b)/2
b) 计算f(m)
c) 如果 f(a)f(m)<=0，则令 b=m
否则, 令 a=m
d) 如果 |a-b|<ε,则令 x=m, 结束；否则，继续执行a-c

二分法的代码如下：

function root = Erfen(f, a, b, epsilon)
%功能：二分法求非线性方程f（x）=0的根
%输入参数：
%f是表示非线性函数f（x）的参数（变量），数据类型：函数句柄对象
%a--区间左端点， b--区间右端点， epsilon--控制精度的参数
%输出参数
%root--非线性方程f（x）= 0在[a, b]内的根
if f(a)*f(b)>0
    root=NaN;      %无解
    return
end

while b-a>epsilon
    m=(a+b)/2;
    if f(a)*f(m)<=0
        b=m;
    else
        a=m;
    end
end

root=(a+b)/2;

end

函数调用如下：

>> f=@(x) x^3-2*x-5;
>> root=Erfen(f,2,3,1e-6)

root =

    2.0946

2.迭代法

在这里插入图片描述

【例】用迭代法求方程 x^3 - x - 1 = 0在x=1.5 附近的一个根。

分析：可以将方程改写成如下两种等价形式：
x = $\phi$ 1(x) = $\sqrt[3]{x + 1}$ ????????????????(1)
x = $\phi$ 2(x) = x³ - 1????????????????????? (2)
相应地可以得到两个迭代公式:
$x_{k+1}$ = $\phi$ 1 ( $x_{k}$ ) = $\sqrt[3]{xk + 1}$
$x_{k+1}$ = $\phi$ 2 ( $x_{k}$ ) = $x_{k}$ ³ - 1

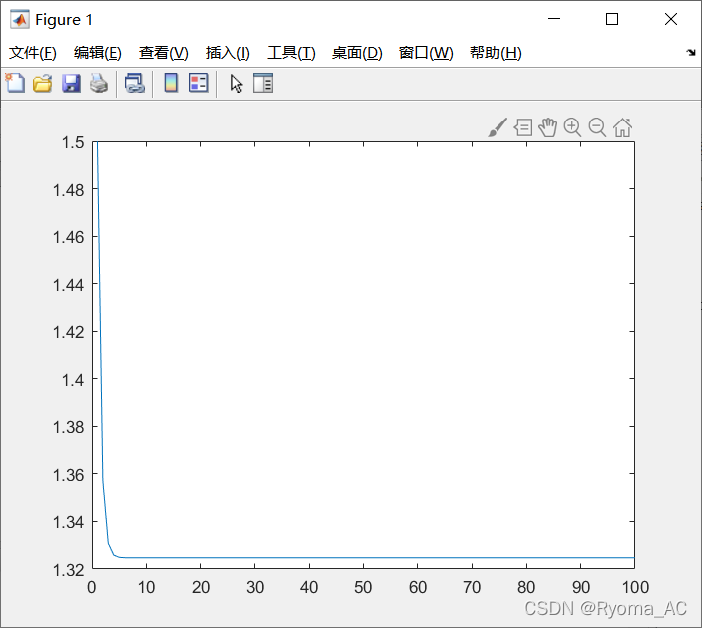
通过编写代码画图我们可以看到

%x(k+1)=(x(k)+1) ^(1/3) ——收敛
x=zeros(1,100);
x(1)=1.5;
for k=1:99
    x(k+1)=(x(k)+1) ^(1/3);
end
plot(x)

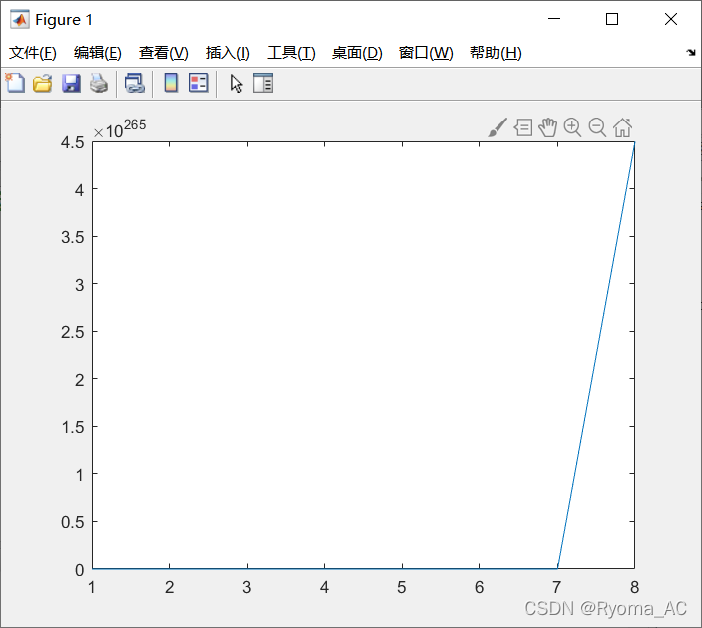
在这里插入图片描述

%x(k+1) = x(k) ^3 - 1;  ——不收敛
x=zeros(1,100);
x(1)=1.5;
for k=1:99
    x(k+1) = x(k) ^3 - 1;
end
plot(x)

在这里插入图片描述
通过命令控制台查看 x 的向量的收敛值便可得到根的值

3.MATLAB内置求解方程函数

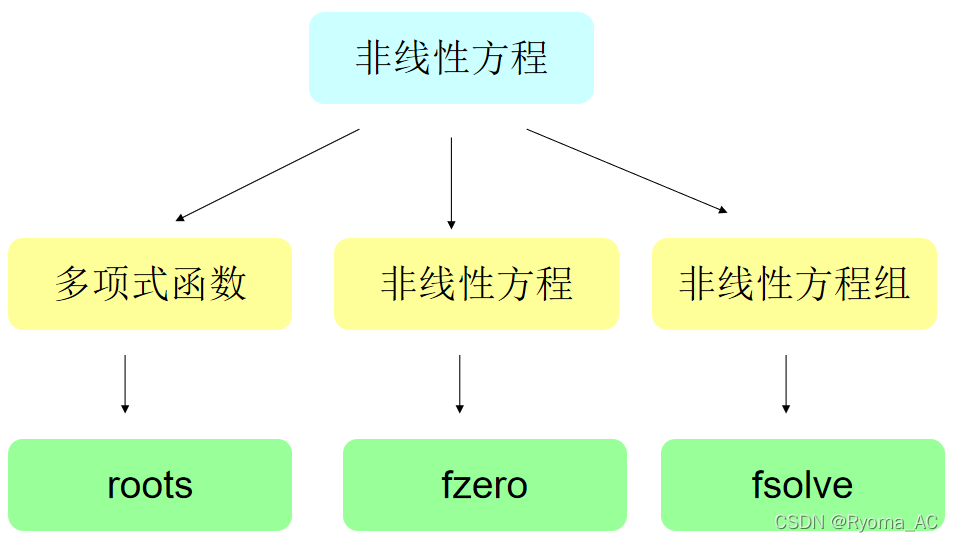
在这里插入图片描述

1）roots函数

对于多项式函数来说
Matlab提供了多种多项式计算函数，如
求多项式的值，polyval；
多项式乘法，conv；
多项式除法，deconv；
多项式微分，polyder；
多项式拟合，polyfit；
多项式求根函数， roots

r = roots( c )，用于求解多项式的根
其中，行向量c的元素是多项式的系数，按多项式次数降序排列
如果c中含有n+1个元素，则多项式为n次
roots可以获得多项式的所有根
其算法为计算伴随矩阵的特征值

>> %求x^3=x^2+1 
>> %f(x) = x^3 - x^2 -1 = 0 
>> c=[1, -1, 0, -1 ]

c =

     1    -1     0    -1

>> r=roots(c)

r =

   1.4656 + 0.0000i
  -0.2328 + 0.7926i
  -0.2328 - 0.7926i

>> polyval(c,r)

ans =

   1.0e-15 *

   0.4441 + 0.0000i
   0.2220 + 0.1110i
   0.2220 - 0.1110i

2）fzero函数

fzero
对于一般的单个超越方程，可以采用fzero函数求解
fzero函数结合使用二分法、割线法和可逆二次内插法
其用法大致为：

>> x=fzero(@sin,3)

x =

    3.1416

>> format long
>> x

x =

   3.141592653589793

>> x=fzero(@cos,[1,2])

x =

   1.570796326794897

>> x=fzero(@cos,[0, 2*pi])

错误使用 fzero (line 290)
区间端点处的函数值必须具有不同的符号。

>> x=fzero(@(x)x^3-2*x-5,1)

x =

   2.094551481542327

3）fsolve函数

%用fslove求解线性方程组
%sin(x)+y^2+log(z)=7
%3*x+2^y-z3+1=0
%x+y+z=5
%方法：
%1.首先把方程组写成F(X)=0这种形式
%2.定义函数Y=F（X）
%F(X)的输入参数是由所有未知数构成的向量，在本例题中X=[ x, y, z]
%输出参数（函数值）Y是列向量
%Y(i)是当X=[x, y, z]给定时，第i个方程的左边减去右边的值
%3.调用fslove求解方程组的解

function Y=test_fun3(X)
%输入参数X表示由方程组的未知数[ x, y, z]构成的向量
%输出参数Y是一个列向量，Y(i)=第i个方程的左端减右端
x=X(1);
y=X(2);
z=X(3);
Y=[sin(x)+y^2+log(z)-7;3*x+2^y-z^3+1;x+y+z-5];
end

函数调用求解代码：

>> x0 = [1 1 1];
>> x=fsolve(@test_fun3,x0)
x =

   0.599053756637426   2.395931402383216   2.005014840979314

随笔

今天又是匆匆忙绿的一天，探望很久没见的老师，理掉了好久没理的头发，办理了快要过期的身份证，更换了佩戴好久的眼镜，陪老朋友吃饭叙了好久的旧……缓过头来才意识到，今天是2021的最后一天。今天和朋友叙旧，谈到了曾经的时光，那时候我们有梦，关于文学，关于爱情，关于穿越世界的旅行，如今我们开始饮酒，杯子碰到一起，都是梦破碎的声音。时常会刷到朋友圈中，曾经的好友光鲜亮丽的美好生活，羡慕着他们找到了自己的生活方式，与此同时，也伴随着自身的迷茫与苦涩。不知从什么时候开始，自己便像一个上了发条的玩具，不断地奔跑，不断地前进，遗落了曾经拥有的，追寻着虚无缥缈的。或许是身上被寄予了太多的期望，在前进疲惫的路上总是感觉到分外的压力。人们总说，人心的偏见像一座大山，压得人喘不过气，人类的期望又何尝不是如此。屠龙少年终成恶龙，人最终还是活成了别人眼中希望的样子。晚上走在灯火通明的街道，我与节日的祥瑞与和谐显得格格不入，2021发生了太多的事情，一场疫情改变了所有人的生活，我已经快忘记没有疫情的日子了，就像是我不曾记起儿时对过年的欣喜与期盼。不知道为什么，今天的自己心情那么低落，就让糟糕的心情留在今年吧，新年快乐，明年再见。