[数据结构与算法]week07_task_贪心动规

七、贪心动规

来源

极客时间2021算法训练营

作者: 李煜东

1 贪心

1.1 基本思想

贪心算法(GreedyAlgorithm)是一种
(1)在每一步选柽中都采取在当前状态下的最优决策(局部最优)
(2)并希望由此导致的最终结果也是全局最优
的算法

• 贪心和动规不同: 不对整个状态空间进行 遍历或计算，而是始终按照局部最优选择执行下去，不再回头。

• 状态空间角度: 贪心算法实际上是在状态空间中按局部最优策略找了一条路径。

• 使用贪心法要求问题的整体最优性可以由局部最优性导出。贪心算法的正确性需要证明, 常见的证明手段有:

  • 微扰 (邻项交换)
    证明在任意局面下, 任何对局部最优策略的微小改变都会造成整体结果变差。经常用于以 “排序” 为贪心策略的证明。
  • 范围缩放(拓展范围)
    证明任何对局部最优策略作用范围的扩展都不会造成整体结果变差。
  • 决策包容性
    证明在任意局面下, 作出局部最优决策以后, 在问题状态空间中的可达集合包含了作出其他任何决策后的可达集合。换言之, 这个局部最优策略提供的可能性包含其他所有策略提供的可能性。
  • 反证法
  • 数学归纳法

• 例子
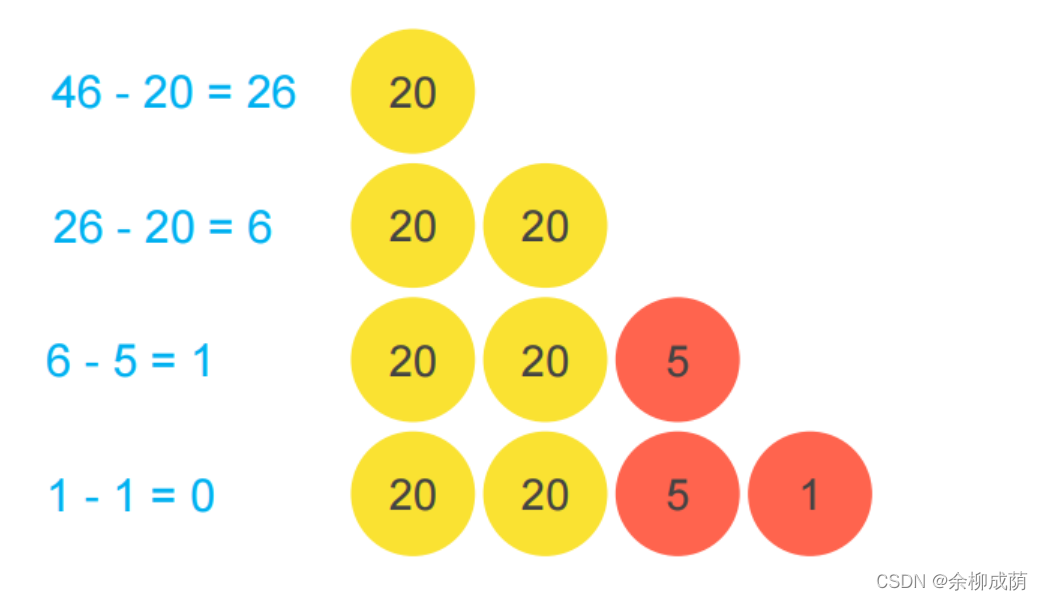
  零钱兑换：贪心
  根据我们平时找钱的思路，一般我们会先考虑面值大的，零钱再用面值小的凑齐 “每次都选尽量大的面值” 就是一个贪心思想

1.2 相关例题

1.2.1 860 . 柠檬水找零

• 思路: 动态维护币值数量 >>>> 贪心: 先找面值大的

class Solution:
    def lemonadeChange(self, bills: List[int]) -> bool:
        dic = defaultdict(int)
        for bill in bills:
            dic[bill] += 1
            curr = bill - 5
            for money in [10, 5]:  #从找10元开始考虑
                while curr >= money and dic[money] > 0:
                    dic[money] -= 1
                    curr -= money
            if curr != 0:
                return False
        return True

1.2.2 455 . 分发饼干

• 思路: 贪心 >>> 大饼先满足需求大的孩子g[i], 剩下更易满足

决策包容性证明:贪心局部最佳>>全局最佳：一块饼干总是想要满足一个孩子的，满足胃口更大的孩子，未来的可能性包含了满足 胃口更小孩子的可能性

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        count,ans = 0, 0
        for child in g:
            while count < len(s) and s[count] < child:
                count += 1
            if count < len(s):
                ans += 1
                count += 1
        return ans

1.2.3 122 . 买卖股票的最佳时机 II

• 思路: 获得所有prices[i] - prices[i - 1] > 0区间的收益
  决策范围扩展
  在思考贪心算法时，有时候不容易直接证明局部最优决策的正确性 此时可以往后多扩展一步，有助于对当前的决策进行验证

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        ans = 0
        for i in range(1, len(prices)):
            ans += max(prices[i] - prices[i-1], 0)
        return ans

1.2.4 45 . 跳跃游戏 II

• 思路: 查看后两步的可能性
  决策包容性：同样都是跳1步，从a跳到"能跳得更远"的b,未来的可达集合包含了跳到其他 b的可达集合，所以这个局部最优决策是正确的。

class Solution:
    def jump(self, nums: List[int]) -> int:
        ans, now = 0, 0
        while now < len(nums) - 1:
            right = now + nums[now]  # right是now位置能达到最大位置
            if right >= len(nums) - 1:
                return ans +1
            nextNow = now
            nextRight = right
            for i in range(now + 1, right + 1): # now 可以达到范围[now + 1, right]
                if i + nums[i] > nextRight:        #使得 now下下个可达位置最远
                    nextNow = i
                    nextRight = i + nums[i]
            now = nextNow
            ans += 1
        return ans

1.2.5 1665 . 完成所有任务的最少初始能量

邻项交换
经常用于以某种顺序"排序"为贪心策略的证明
证明在任意局面下，任何局部的逆序改变都会造成整体结果变差

• 思路: 需要求顺序 >>> 动规 二分需排序 >>> 贪心 >>> 门槛(task[1])高 具有较优先趋势, 能耗(task[0])低同样具有较优先趋势 >>> 考虑task[0] - task[1]升序排序

证明:
设task[0]为actual, task[1]为minimum;
设做完第i+2到n个任务所需的初始能量最少为S ;
对于两个相邻任务：设第i个和第i+l个完成的任务分别是p和q:

考虑$p,q$中先做者所需要的最低能量$S_p,S_q$:
先做p, 所需要能量:
$$S_p=max(max(minimum[q],S+actual[q])+actual[p],minimum[p])$$
$$=max(minimum[q]+actual[p],S+actual[q]+actual[p],minimum[p])$$
先做q, 所需要能量:
$$S_q=max(max(minimum[p],S+actual[p])+actual[q],minimum[q])$$
$$=max(minimum[p]+actual[q],S+actual[p]+actual[q],minimum[q])$$

P优先则 >>> 满足 $S_p<S_q$ 即:
$$max(minimum[q]+actual[p],minimum[p])<max(minimum[p]+actual[q],minimum[q])$$

因为必定有 $minimum[q]+actual[p]>minimum[q]$
所以上式等价于 $minimum[q]+actual[p]<minimum[p]+actual[q]$
即 $actual[p]?minimum[p]<actual[q]?minimum[q]$

于是有: >>>贪心策略：按照actual - minimum升序排序，以此顺序完成任务

class Solution:
    def minimumEffort(self, tasks: List[List[int]]) -> int:
        ans = 0
        tasks.sort(key = lambda x: x[0] - x[1])
        for task in tasks[::-1]:   #倒序考虑完成所需要能量
            ans = max(task[1], ans + task[0])
        return ans

2 线性动规

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

• 即 >>> 搜索的优化

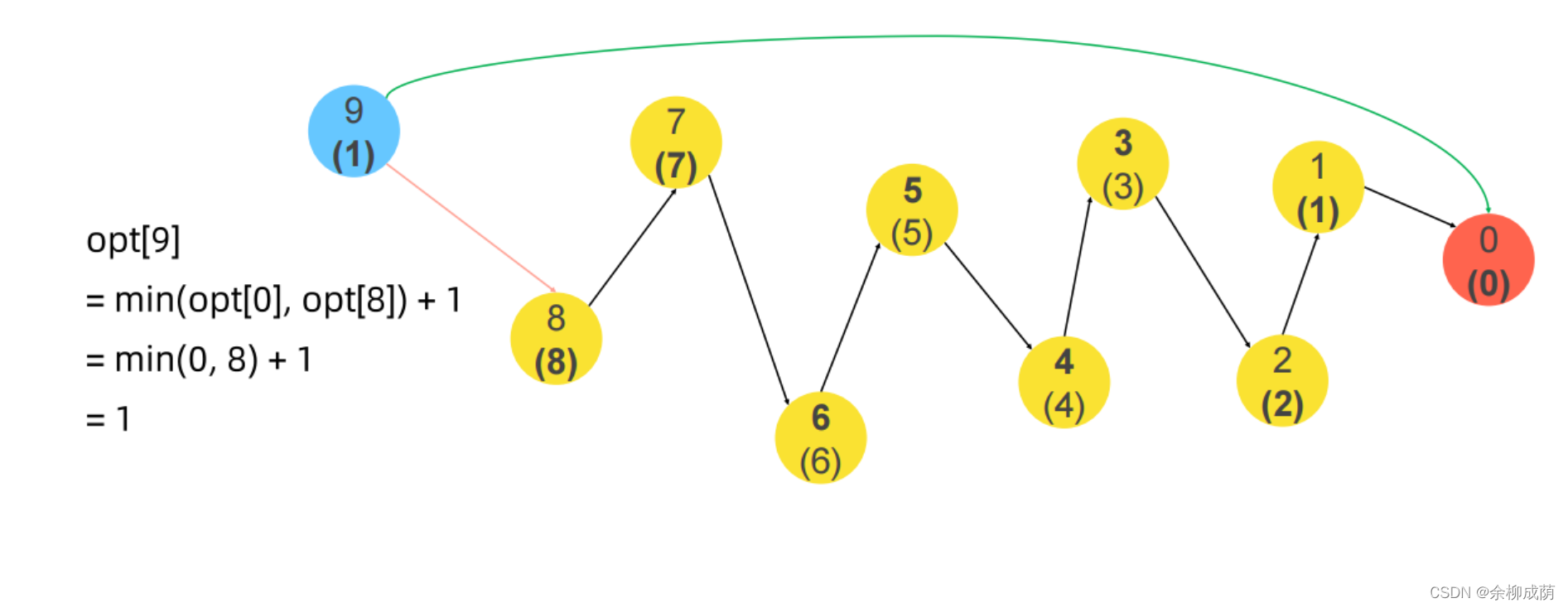
• 对于零钱兑换问题(amount = 18, coins = [10, 9, 1])的状态空间:

  • opt(n) = min(opt(n - 1), opt(n - 9),opt(n - 10)) + 1
    

  • 式子本质: 状态+最优化目标+最优化目标之间具有递推关系=最优子结构

动态规划(DP, dynamic programming)是一种对问题的状态空间进行分阶段、有顺序、不重复、 决策性遍历的算法

• 动态规划的关键与前提：
  重叠子问题——与递归、分治等一样，要具有同类子问题，用若干维状态表示
  最优子结构 ——状态对应着一个最优化目标，并且最优化目标之间具有推导关系
  无后效性——问题的状态空间是一张有向无环图(可按一定的顺序遍历求解)

• 动态规划一般采用递推的方式实现
  也可以写成递归或搜索的形式，因为每个状态只遍历一次，也被称为记忆化搜索

• 动态规划三要素：阶段、状态、决策

2.1 相关题目

2.1.1 63 . 不同路径 II

• 思路: dfs在此计数问题由于方案数 * 方案数 >>> 时间复杂度较大 >>> 递归,分治思想 >>> 记忆化搜索 >>> 减小时间复杂度

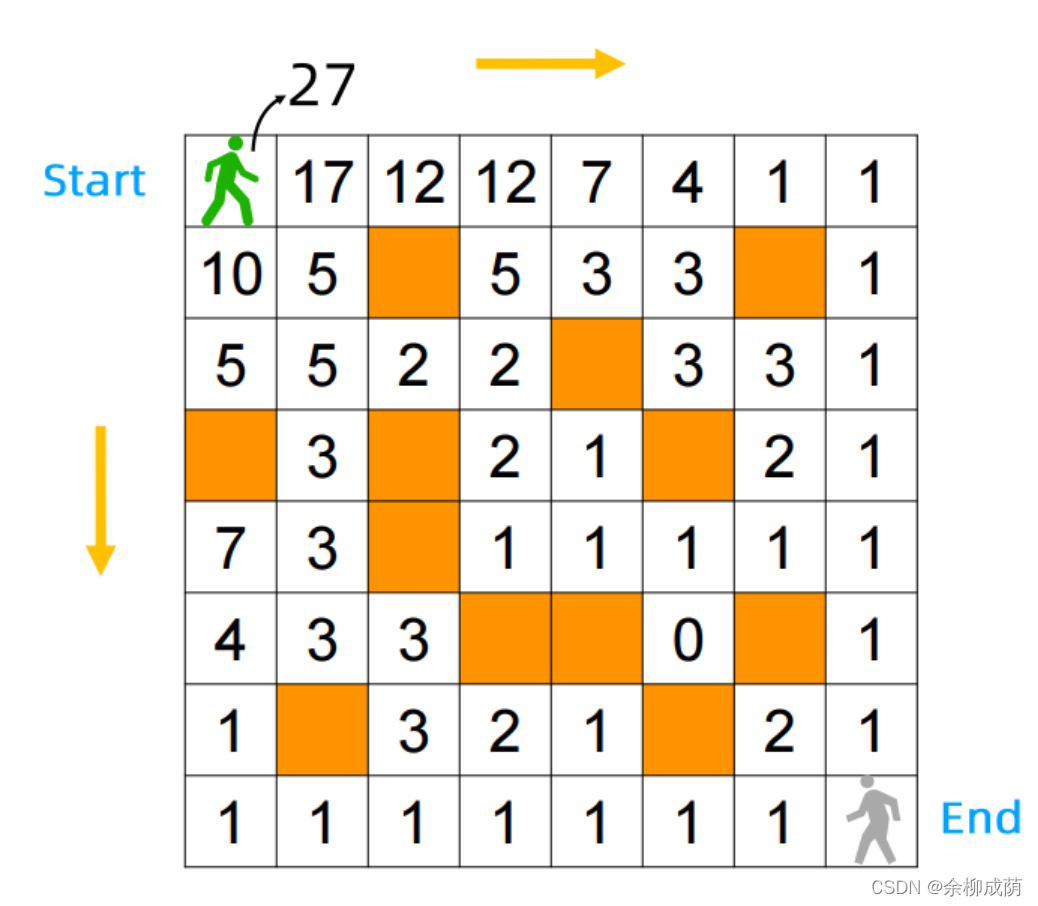
Bottom-up
f[i,j]表示从(i,j)到End的路径数, 如果(i,j)是空地,f[i,j] = f[i + l,j] + f[i,j + 1]
否则f[i,j] = 0

反过来类似的:

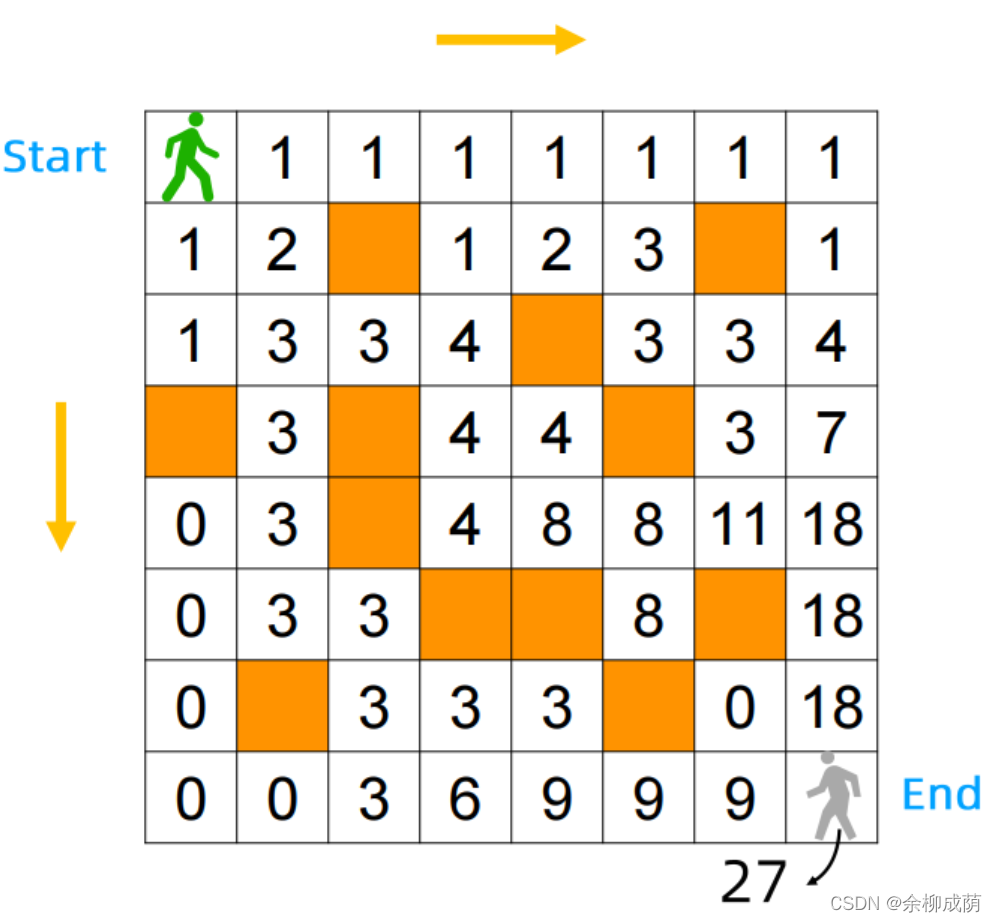
Top-down
f[i,j]表示从Start到(i，j)的路径数, 如果(i,j)是空地,f[i,j] = f[i - 1,j] + f[i,j - 1]

否则f[i,j] = 0

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m, n = len(obstacleGrid), len(obstacleGrid[0])
        f = [[0]*n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if obstacleGrid[i][j] == 1:
                    f[i][j] = 0
                elif i == 0 and j == 0:
                    f[i][j] = 1
                elif i == 0:
                    f[i][j] = f[i][j - 1] 
                elif j == 0:
                    f[i][j] = f[i - 1][j]
                else:
                    f[i][j] = f[i - 1][j] + f[i][j - 1]
        return f[-1][-1]

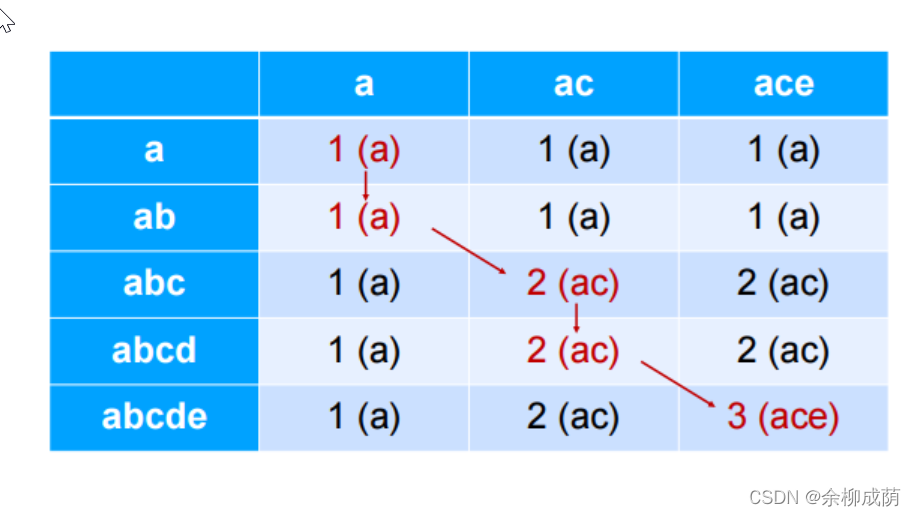
2.1.2 1143 . 最长公共子序列

• 思路: 只关心数量>>> 动规 >>> 观察蛮力搜索状态 >> 寻找变化信息 >>> 确定最优子结构, 边界

f[i][j]表示text1的前i个字符和text2的前j个字符能组成的LCS的长度
如果 text1[i] = text2[j]: f[i][j] = f[i - 1][j-1] + 1
如果 text1[i] != text2[j]: f[i][j] = max(f[i - 1][j], f[i][j-1] )

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m, n = len(text1), len(text2)
        f = [[0]*(n + 1) for _ in range(m + 1)]
        text1 = " " + text1   #防止i-1, j-1越界
        text2 = " " + text2
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i] == text2[j]:
                    f[i][j] = f[i - 1][j - 1] + 1
                else:
                    f[i][j] = max(f[i - 1][j], f[i][j - 1])
        return f[-1][-1]

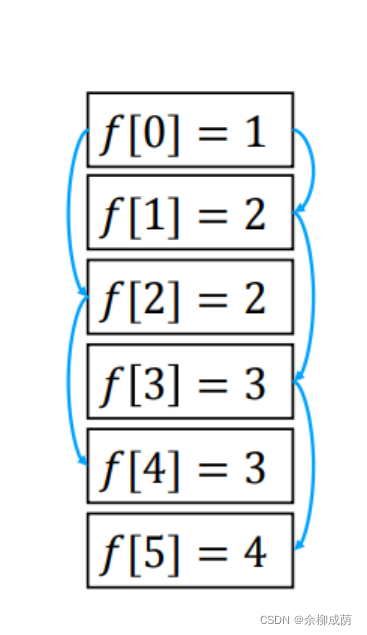
2.1.3 300 . 最长递增子序列

• 思路: 指数级别状态空间(子集 >> 选或不选) >>> 在每一状态只关心结尾数值 以及 选择个数

f[i]表示前i个数构成的以a[i]为结尾的最长上升子序列的长度

f [ i ] = max ? j < i , a [ j ] < a [ i ] { f [ j ] + 1 } f[i]=\max _{j<i, a[j]<a[i]}\{f[j]+1\} f[i]=j<i,a[j]<a[i]max?{f[j]+1}

边界：f[i] = 1 (0 <= i < n)
目标： max ? 0 ≤ i < n { f [ i ] } \max _{0 \leq i<n}\{f[i]\} max0≤i<n?{f[i]}

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        n, ans = len(nums), 0
        f = [1 for _ in range(n)]
        for i in range(1, n):
            for j in range(i):
                if nums[i] > nums[j]:
                    f[i] = max(f[j] + 1, f[i])
        for k in range(n):
            ans = max(ans, f[k])
        return ans

• 假如记下路径

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        n, ans,curr,end = len(nums), [], 0, -1
        f = [1 for _ in range(n)]
        pre = [-1 for _ in range(n)]
        def p(i):
            if pre[i] != -1:
                p(pre[i])
            ans.append(nums[i])
        for i in range(1, n):
            for j in range(i):
                if nums[i] > nums[j] and f[i] < f[j] + 1 :
                    f[i] = f[j] + 1
                    pre[i] = j
        for k in range(n):
            if f[k] > curr:
                end = k
        p(end)
        return ans

2.1.4 53 . 最大子数组和

𝑓[𝑖] 表示以 𝑖 为结尾的最大子序和
𝑓 [𝑖] = max (𝑓 [𝑖 ? 1] + 𝑛𝑢𝑚𝑠 [𝑖] , 𝑛𝑢𝑚𝑠[𝑖])

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        ans = nums[0]
        f = [nums[0] for _ in range(n)]
        for i in range(1, n):
            f[i] = max(nums[i], f[i-1] + nums[i])
        for i in range(1, n):
            ans = max(ans, f[i])
        return ans

2.1.5 152 . 乘积最大子数组

• 思路:
  考虑到负负得正情况, 不能只考虑当前乘积最大作为最优:
  max和min一起作为代表，才满足最优子结构！
  𝑓𝑚𝑎𝑥 [𝑖 ] , 𝑓𝑚𝑖𝑛[𝑖] 表示以 𝑖 为结尾的乘积最大、最小子数组
  𝑓𝑚𝑎𝑥[ 𝑖 ]= max (𝑓𝑚𝑎𝑥 [𝑖 ? 1 ]? 𝑛𝑢𝑚𝑠 [𝑖] , 𝑓𝑚𝑖𝑛 [𝑖 ? 1] ? 𝑛𝑢𝑚𝑠 [𝑖] , 𝑛𝑢𝑚𝑠[𝑖])
  𝑓𝑚𝑖𝑛[ 𝑖 ]= min (𝑓𝑚𝑎𝑥 [𝑖 ? 1] ? 𝑛𝑢𝑚𝑠 [𝑖] , 𝑓𝑚𝑖𝑛 [𝑖 ? 1] ? 𝑛𝑢𝑚𝑠 [𝑖] , 𝑛𝑢𝑚𝑠[𝑖])

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        n = len(nums)
        ans = nums[0]
        fmin = [nums[0] for _ in range(n)]
        fmax = [nums[0] for _ in range(n)]
        for i in range(1, n):
            fmax[i] = max(nums[i], fmax[i-1] * nums[i], fmin[i-1] * nums[i])
            fmin[i] = min(nums[i], fmax[i-1] * nums[i], fmin[i-1] * nums[i])
        for i in range(1, n):
            ans = max(ans, fmax[i])
        return ans

3 作业

3.1 70 . 爬楼梯

• 思路: n阶上一位n-1或n-2 : f(n) = f(n-1) + f(n-2)

class Solution:
    def climbStairs(self, n: int) -> int:
        f = [0 for _ in range(n + 1)]
        f[0] = f[1] = 1
        for i in range(2, n + 1):
            f[i] = f[i - 1] + f[i - 2]
        return f[-1]

3.2 120 . 三角形最小路径和

• 思路: 从下至上构建 f[i - 1][j] = triangle[i - 1][j] + min(f[i][j], f[i][j + 1])

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        f = [[0]* (i + 1) for i in range(len(triangle))]
        f[-1] = triangle[-1]
        for i in range(len(triangle) - 1, 0, -1):
            for j in range(len(triangle[i])-1):
                f[i-1][j] = triangle[i - 1][j] + min(f[i][j], f[i][j + 1])
        return f[0][0]

3.3 673 . 最长递增子序列的个数

• 思路: 和300题类似, 不过记得需要绩效个数

class Solution:
    def findNumberOfLIS(self, nums: List[int]) -> int:
        if len(nums) == 1:return 1
        n = len(nums)
        max_len, ans = 0, 0
        f = [1 for _ in range(n)]   # 递增序列长度
        count = [1 for _ in range(n)]  # 递增序列的个数
        for i in range(1, n):
            for j in range(i):
                if nums[i] > nums[j] and f[i] < f[j] + 1: #若当前长度大于之前记录长度 更新长度
                    f[i] = f[j] + 1
                    count[i] = count[j]
                elif nums[i] > nums[j] and f[i] == f[j] + 1: #若历史长度与某一当前j长度一致 更新count
                    count[i] += count[j]
            max_len = max(max_len, f[i])
        for i in range(n):
            if f[i] == max_len:
                ans += count[i]
        return ans

参考资料

1. https://cloud.tencent.com/developer/article/1817113看一遍就理解：动态规划详解
2. <>