MATLAB是一个很强大的软件,在自动控制领域也是使用非常广泛,本系列博文将基于控制系统仿真进行,参考书籍《MATLAB/Simulink与控制系统仿真》,该系列博文与笔者的自动控制理论(考研篇)互为补充,详细理论知识点请各位移步自动控制理论(考研篇)系列博客。
21.系统模型转换及连接
21.1 模型转换
线性时不变系统(LTI)模型包括:传递函数(Transfer Function)模型,零极点增益(ZPK)模型,状态空间(State Space)模型;
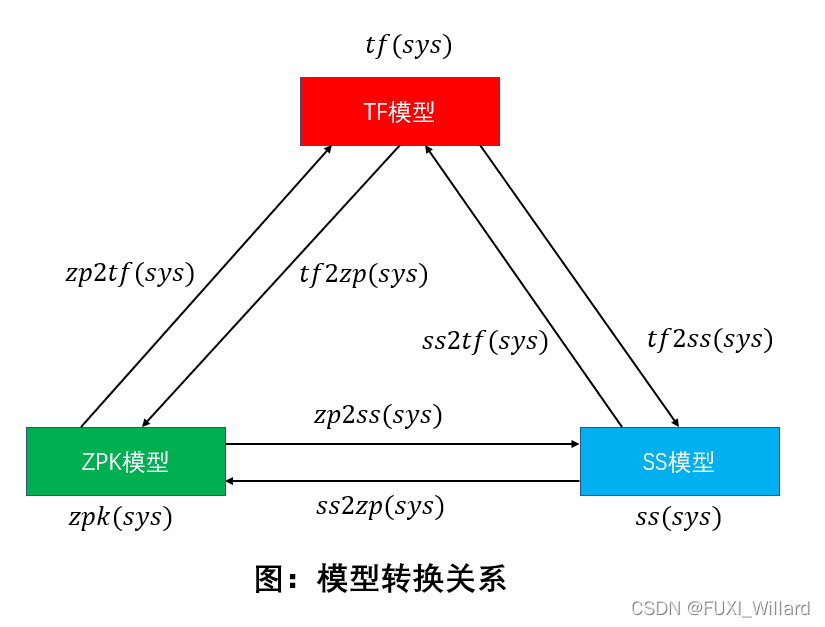
| 函数名 | 功能 | 函数名 | 功能 |
|---|---|---|---|
| ss2tf | 状态空间模型转换为传递函数模型 | tf2ss | 传递函数模型转换为状态空间模型 |
| ss2zp | 状态空间模型转换为零极点模型 | zp2ss | 零极点模型转换为状态空间模型 |
| tf2zp | 传递函数模型转换为零极点模型 | zp2tf | 零极点模型转换为传递函数模型 |
21.2 实战
实战:已知某系统零极点模型为:
G
(
s
)
=
6
(
s
+
2
)
(
s
+
1
)
(
s
+
3
)
(
s
+
5
)
G(s)=\frac{6(s+2)}{(s+1)(s+3)(s+5)}
G(s)=(s+1)(s+3)(s+5)6(s+2)?
求其传递函数模型和状态空间模型;
解:
% model_transfer.m文件
z = [-2];p = [-1,-3,-5];k = 6; % 系统零极点向量及增益
[num,den] = zp2tf(z,p,k); % 零极点模型转换成传递函数模型
[A,B,C,D] = zp2ss(z,p,k); % 零极点模型转换成状态空间模型
g_zpk = zpk(z,p,k) % 建立零极点模型
g_tf = tf(num,den) % 建立传递函数模型
g_ss = ss(A,B,C,D) % 建立状态空间模型
% 结果:
g_zpk =
6 (s+2)
-----------------
(s+1) (s+3) (s+5)
g_tf =
6 s + 12
-----------------------
s^3 + 9 s^2 + 23 s + 15
g_ss =
A =
x1 x2 x3
x1 -1 0 0
x2 1 -8 -3.873
x3 0 3.873 0
B =
u1
x1 1
x2 1
x3 0
C =
x1 x2 x3
y1 0 0 1.549
D =
u1
y1 0
21.3 模型连接
基本连接方式:串联、并联、反馈、闭环。
21.3.1 串联
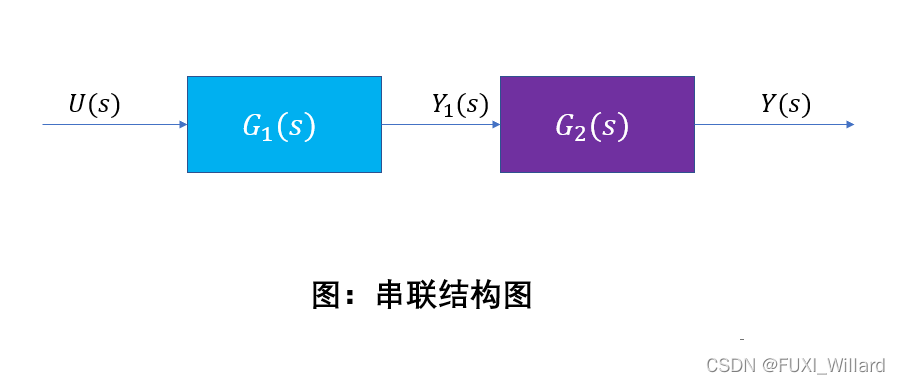
- G 1 ( s ) 、 G 2 ( s ) G_1(s)、G_2(s) G1?(s)、G2?(s)串联连接合成的系统的传递函数为 G ( s ) = G 1 ( s ) ? G 2 ( s ) G(s)=G_1(s)·G_2(s) G(s)=G1?(s)?G2?(s);
[num,den] = series(num1,den1,num2,den2);- 其中:num1、den1为系统 G 1 ( s ) G_1(s) G1?(s)的传递函数的分子和分母多项式;num2、den2为系统 G 2 ( s ) G_2(s) G2?(s)的传递函数的分子和分母多项式;num、den为串联后的系统 G ( s ) G(s) G(s)的传递函数的分子和分母多项式;
21.3.2 并联
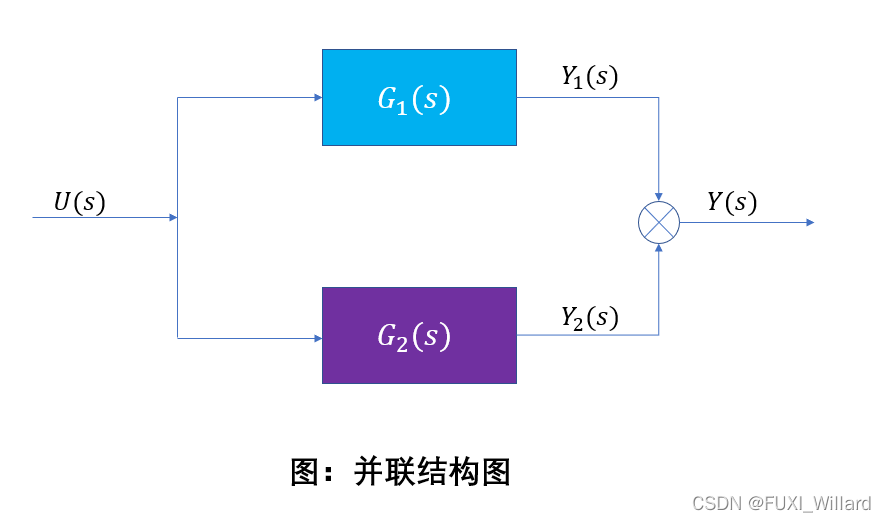
- G 1 ( s ) 、 G 2 ( s ) G_1(s)、G_2(s) G1?(s)、G2?(s)并联合成的系统的传递函数为: G ( s ) = G 1 ( s ) + G 2 ( s ) G(s)=G_1(s)+G_2(s) G(s)=G1?(s)+G2?(s);
[num,den] = parallel(num1,den1,num2,den2);- 其中:num1、den1为系统 G 1 ( s ) G_1(s) G1?(s)的传递函数的分子和分母多项式;num2、den2为系统 G 2 ( s ) G_2(s) G2?(s)的传递函数的分子和分母多项式;num、den为串联后的系统 G ( s ) G(s) G(s)的传递函数的分子和分母多项式;
21.3.3 反馈连接
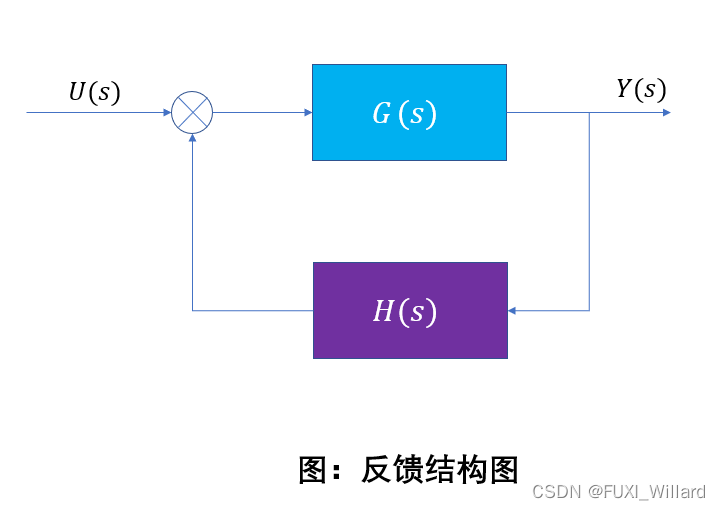
- 正反馈连接的传递传递函数为:
G H ( s ) = G ( s ) H ( s ) 1 ? G ( s ) H ( s ) GH(s)=\frac{G(s)H(s)}{1-G(s)H(s)} GH(s)=1?G(s)H(s)G(s)H(s)? - 负反馈连接的传递函数为:
G H ( s ) = G ( s ) H ( s ) 1 + G ( s ) H ( s ) GH(s)=\frac{G(s)H(s)}{1+G(s)H(s)} GH(s)=1+G(s)H(s)G(s)H(s)? [num,den]=feedback(num1,den1,num2,den2,sign);- num1、den1为系统G(s)的传递函数分子和分母多项式;num2、den2为系统H(s)的传递函数的分子和分母多项式;sign表示负反馈还是正反馈,默认为sign=-1;num、den为反馈连接后的系统的传递函数的分子和分母多项式;
21.4 模型连接实战
实战1:控制系统如下,求系统的串联和并联时的传递函数。
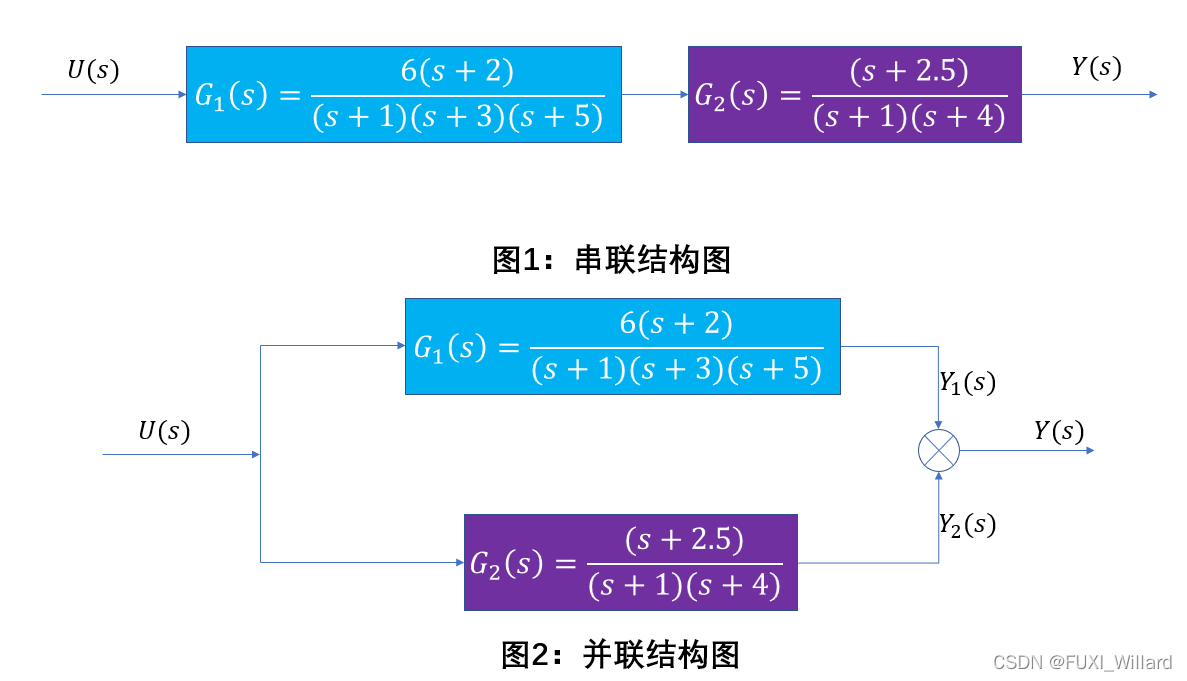
代码实现:
% series_and_parallel.m文件
% 系统1的分子分母向量
num1 = 6*[1,2];
den1 = conv([1,1],conv([1,3],[1,5]));
% 系统2的分子分母向量
num2 = [1,2.5];
den2 = conv([1,1],[1,4]);
% 构建串联和并联的分子分母向量
[nums,dens] = series(num1,den1,num2,den2);
[nump,denp] = parallel(num1,den1,num2,den2);
% 生成串联和并联的传递函数
s_tf = tf(nums,dens);
p_tf = tf(nump,denp);
s_tf,p_tf
% 结果:
s_tf =
6 s^2 + 27 s + 30
--------------------------------------------
s^5 + 14 s^4 + 72 s^3 + 166 s^2 + 167 s + 60
p_tf =
s^4 + 17.5 s^3 + 87.5 s^2 + 156.5 s + 85.5
--------------------------------------------
s^5 + 14 s^4 + 72 s^3 + 166 s^2 + 167 s + 60
实战2:系统如下图所示,求下图的闭环传递函数和反馈传递函数;
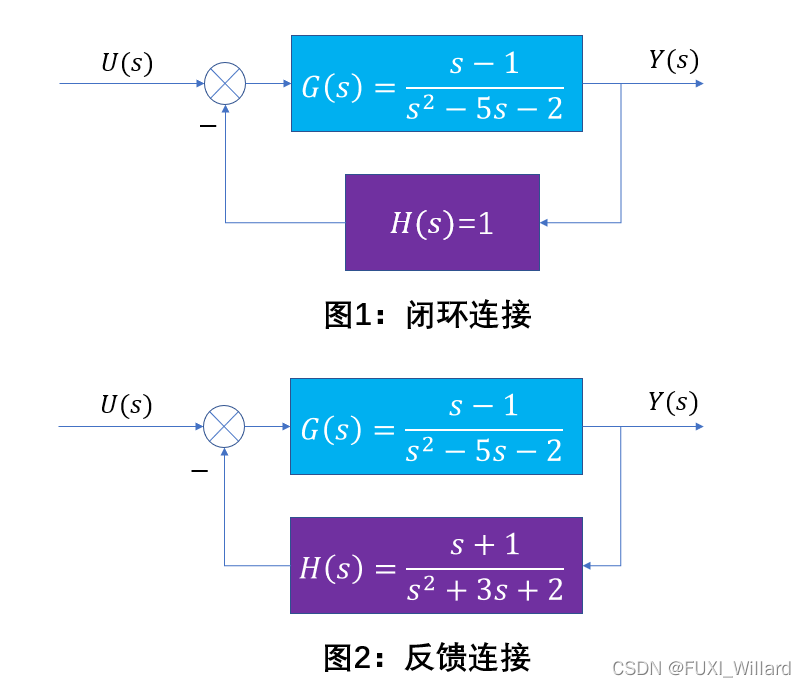
代码实现:
% feedback_cloop.m文件
% 系统1
num1 = [1,-1];
den1 = [1,-5,-2];
% 系统2
num2 = [1,1];
den2 = [1,3,2];
% 闭环连接系统和反馈连接系统
[numc,denc] = cloop(num1,den1);
[numf,denf] = feedback(num1,den1,num2,den2);
% 闭环连接传递函数和反馈连接传递函数
c_tf = tf(numc,denc);
f_tf = tf(numf,denf);
c_tf,f_tf
% 结果:
c_tf =
s - 1
-------------
s^2 - 4 s - 3
f_tf =
s^3 + 2 s^2 - s - 2
-------------------------------
s^4 - 2 s^3 - 14 s^2 - 16 s - 5