文章目录
一,哈希表(散列表)概念
大话数据结构里面是这样介绍的:
散列表,又称为哈希表(Hash table),采用散列技术将记录存储在一块连续的存储空间中。
在散列表中,我们通过某个函数f,使得存储位置 = f(关键字),这样我们可以不需要比较关键字就
可获得需要的记录的存储位置。
散列技术的记录之间不存在什么逻辑关系,它只与关键字有关联。因此,散列主要是面向查找的存储结构。
其实哈希表就是将数据以他的特征信息为标准,存在一块空间中,当我们要查询某数据时,我们就可以通过该数据的特征信息快速锁定到该数据的位置,从而大大的提高了数据的查询速度。
如下所示,就是一个简单的哈希表
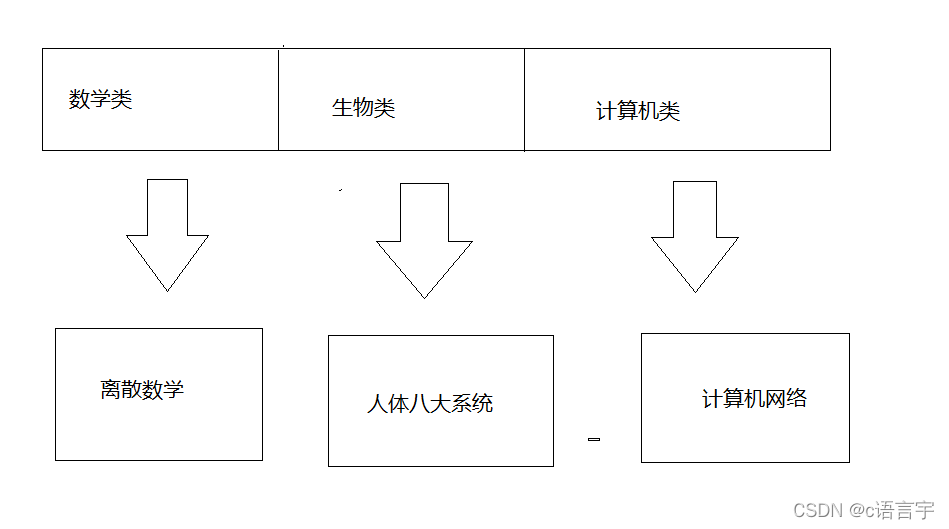
如果我们要找计算机网络这本书,我们可以知道他是计算机类的,所以我们可以直接通过他的特征信息,计算机类
直接找到计算机网络这本书。
二,哈希(散列)函数的构造
哈希(散列)函数的构造原则
1、计算简单
散列函数的计算时间不应该超过其他查找技术与关键字比较的时间。
2、散列地址分布均匀
解决冲突最好的办法就是尽量让散列地址均匀地分布在存储空间中。
保证存储空间的有效利用,并减少为处理冲突而耗费的时间。
构造方法
平方取中法
假设关键字是1234,那么它的平方就是1522756.在抽取中间的3位就是227,用作散列地址。再比如关键字4321,那么它的平方就是18671041,抽中间三位数就是671或710。平方去中法比较适合不知道关键字的分布,而位数又不是很多的情况。
折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(注意最后一部分位数不够时可以短一些),然后将这几部分叠加求和,并按散列表表长,取几位作为散列表地址。
比如我们的关键字是9 8 7 6 5 4 3 2 1 0,散列表表长为3位,我们将它分为四组,
987|654|321|0,然后将他们叠加求和987+654+321+0=1962,再求后3位得到散列地址为962。
有时可能这还不能够保证分布均匀,不妨从一端向另一端来回折叠后对齐相加。比如我们将987和321反转,再与654和0相加,变成789+654+123+0=1566,此时散列地址为566。
折叠法事先不需要知道关键字的分布,适合关键字位数较多的情况。
3## 除留余数法
此方法为最常用的构造散列函数的方法。
公式为
f(key)=key mod p (p<=m)
保留余数法
mod是取模的意思(求余数)
这个很常用,所以就用代码实现一下
//哈希函数
int Hash(int key, int TableSize)
{
return key % TableSize;
}
三,冲突
冲突就是,两个不同的关键字,但是通过散列函数得出来的地址是一样的。
key1 ≠ key2,但是f(key1)= f(key2)
同义词
此时的key1 和key2就被称为这个散列函数的同义词
那可不行啊,一件单人间怎么可以住两个人呢?
别担心,这个问题自然已经被神通广大的大佬们解决了。
处理散列冲突的方法
开放定址法
开发定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只需要散列表足够大,空的散列地址总能找到,并将记录存入
例子:
19 01 23 14 55 68 11 86 37
要存储在表长11的数组中,其中H(key)=key MOD 11
1.线性探测法
公式
f1(key) = (f(key)+d1) MOD m(di=1,2,3,....,m-1)
我们取di等于1
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| key | 55 | 1 | 14 | 19 | 86 | ||||||
| 23冲突 | 23 | ||||||||||
| 68冲突 | 68冲突 | 68 | |||||||||
| 11冲突 | 11冲突 | 11冲突 | 11冲突 | 11冲突 | 11 | ||||||
| 37冲突 | 37冲突 | 37 | |||||||||
| 最终存储结果 | 55 | 1 | 23 | 14 | 68 | 11 | 37 | 19 | 86 |
2.二次探测法
增加平方运算的目的是为了不让关键字都聚再某一块区域,我们称这种方法为二次探测法
公式:
f1(key) = (f(key)+d1) MOD m(di=1^2,-1^2,2^2,-2^2,...,q^2,-q^2,q<=m/2)
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| key | 55 | 1 | 14 | 19 | 86 | ||||||
| 23冲突 | f(23)+1 | ||||||||||
| f(68)-1冲突 | 68冲突 | f(68)+1冲突 | f(68)+4 | ||||||||
| 11冲突 | f(11)+1冲突 | f(11)-1 | |||||||||
| 最终存储结果 | 55 | 1 | 23 | 14 | 68 | 19 | 86 | 11 |
3.随机探测法
在冲突时,对于位移量di采用随机函数计算得到,我们称之为随机探测法
公式
f1(key) = (f(key)+d1) MOD m(di是一个随机数列)
具体方法和上面一样
就不多赘述了
再散列函数法
对于我们的散列表来说,我们事先需要准备多个散列函数
f(key)=RHi(key) (i=1,2...,3)
这里的RHi就是不同的散列函数,每当发生冲突时,就换一个散列函数进行计算,总有一个函数可以将冲突解决
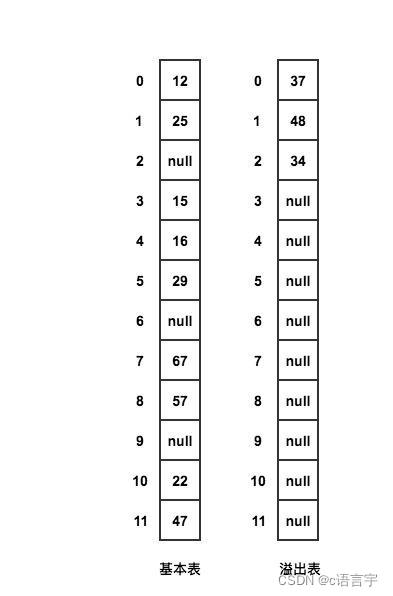
公共溢出区法
在原先基础表的基础上再添加一个溢出表
当发生冲突时,就将该数据放到溢出表中
在查找时,对给定值通过散列函数计算出散列地址后,先与基本表的相应位置进行对比,如果相等就查找成功,如果不相等,则到溢出表进行顺序查找
链地址法
就时用链表将发生冲突的数据链起来,在查找时,只需要遍历链表即可
如下图
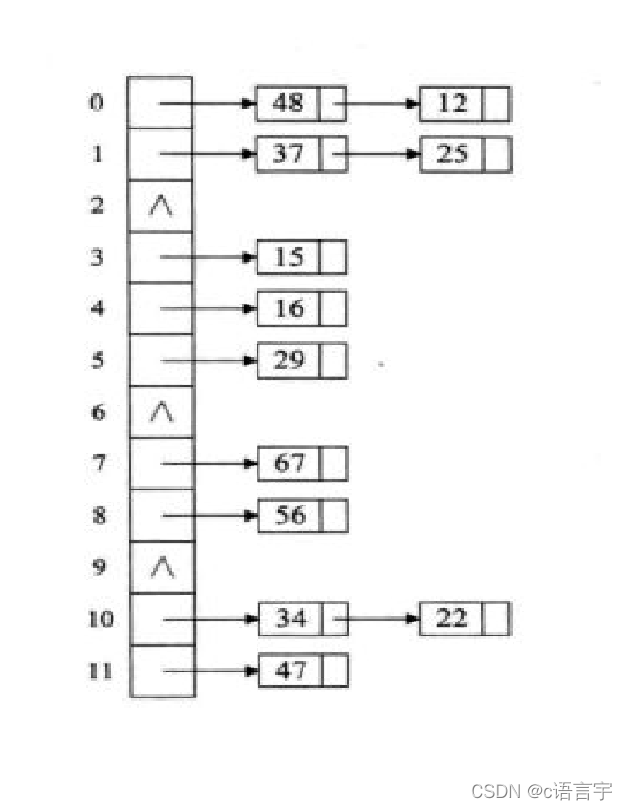
此方法也是我们最长用处理哈希冲突的方法
四,代码实现
1.哈希函数
//哈希函数
int Hash(int key, int TableSize)
{
return key % TableSize;
}
2.链表和哈希表的创建
#define DEFAULT_SIZE 16
typedef int type;
//结点
typedef struct ListNode
{
struct ListNode* next;
int key; //线索
type* data; //数据
}ListNode;
//提高可读性
typedef ListNode* List;
typedef ListNode* Element;
//哈希表
typedef struct HashTable
{
int TableSize;
List* Thelists;
}HashTable;
3.哈希表初始化
HashTable* InitHash(int TableSize)
{
int i = 0;
HashTable* htable = NULL;
if (TableSize <= 0)
{
TableSize = DEFAULT_SIZE;
}
htable = (HashTable*)malloc(sizeof(HashTable));
if (htable == NULL)
{
printf("初始化失败\n");
return NULL;
}
//为桶分配内存空间,其为一个指针数组
htable->Thelists = (List*)malloc(sizeof(List) * TableSize);
if (htable->Thelists == NULL)
{
printf("初始化失败\n");
free(htable);
return NULL;
}
//为Hash桶对应的指针数组初始化链表结点
for (i = 0; i < TableSize; i++)
{
htable->Thelists[i] = (ListNode*)malloc(sizeof(ListNode));
if (htable->Thelists[i] == NULL)
{
printf("初始化失败\n");
free(htable->Thelists);
free(htable);
return NULL;
}
}
}
3.从哈希表中根据key查找元素
Element Find(HashTable* HashTable, int key)
{
int i = 0;
List L = NULL;
Element e = NULL;
i = Hash(key, HashTable->TableSize);
L = HashTable->Thelists[i];
e = L->next;
while (e != NULL && e->key != key)
e = e->next;
return e;
}
4.哈希表插入元素
void Insert(HashTable* HashTable, int key, type* value)
{
Element e = NULL, temp = NULL;
List L = NULL;
e = Find(HashTable, key);
if (e == NULL)
{
temp = (Element)malloc(sizeof(ListNode));
if (temp == NULL)
{
printf("malloc error\n");
return;
}
L = HashTable->Thelists[Hash(key, HashTable->TableSize)];
temp->data = value;
temp->key = key;
L->next = temp;
}
else
printf("the key already exist\n");
}
5.元素删除
void Delete(HashTable* HashTable, int key)
{
Element e = NULL, last = NULL;
List L = NULL;
int i = Hash(key, HashTable->TableSize);
L = HashTable->Thelists[i];
last = L;
e = L->next;
while (e != NULL && e->key != key)
{
last = e;
e = e->next;
}
if (e)
{
last->next = e->next;
free(e);
}
else
{
printf("该元素不存在\n");
}
}
6.哈希表销毁
void Destory(HashTable* HashTable)
{
int i = 0;
List L = NULL;
Element cur = NULL, next = NULL;
for (i = 0; i < HashTable->TableSize; i++)
{
L = HashTable->Thelists[i];
cur = L->next;
while (cur->next != NULL)
{
next = cur->next;
free(cur);
cur = next;
}
}