生活中的索引
MySQL 官方对索引的定义为: 索引(Index) 是帮助 MySQL 高效获取数据的数据结构。 可以得到索引的本质: 索引是数据结构。
上面的理解比较抽象, 举一个例子, 平时看任何一本书, 首先看到的都是目录, 通过目录去查询书籍里面的内容会非常的迅速。
上图就是一本金瓶梅的书, 书籍的目录是按顺序放置的, 有第一节, 第二节它本身就是一种顺序存放的数据结构, 是一种顺序结构。
另外通过目录(索引) , 可以快速查询到目录里面的内容, 它能高效获取数据, 通过这个简单的案例可以理解所以就是高效获取数据的数据结构
再来看一个复杂的情况
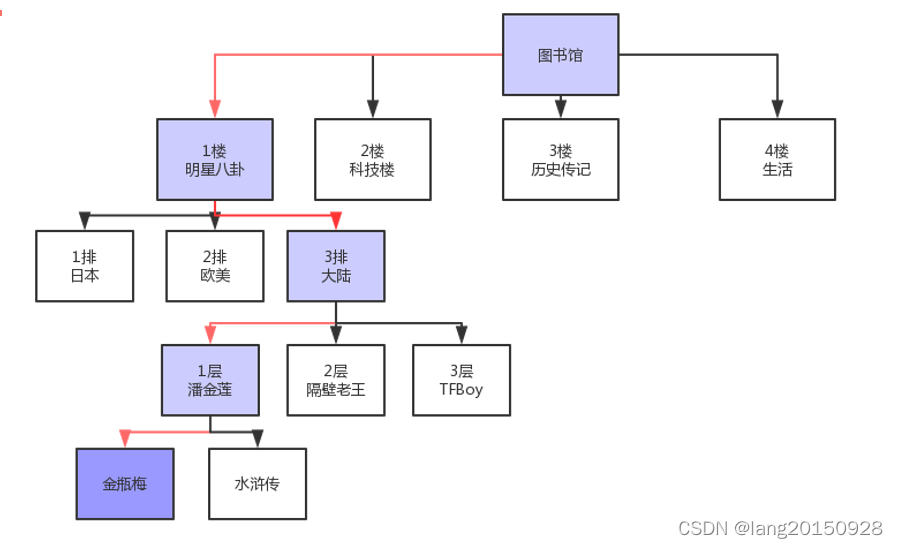
我们要去图书馆找一本书, 这图书馆的书肯定不是线性存放的, 它对不同的书籍内容进行了分类存放, 整索引由于一个个节点组成, 根节点有中间节点, 中间节点下面又由子节点, 最后一层是叶子节点,
可见, 整个索引结构是一棵倒挂着的树, 其实它就是一种数据结构, 这种数据结构比前面讲到的线性目录更好的增加了查询的速度。
MySql 中的索引
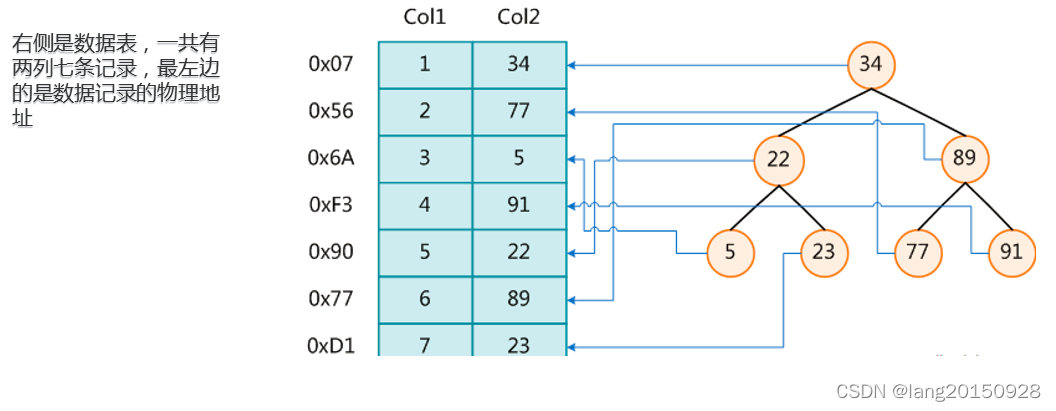
MySql 中的索引其实也是这么一回事, 我们可以在数据库中建立一系列的索引, 比如创建主键的时候默认会创建主键索引, 上图是一种 BTREE 的索引。 每一个节点都是主键的 ID
当我们通过 ID 来查询内容的时候, 首先去查索引库, 查到索引后能快速的根据索引定位数据的具体位置。
所以索引是应用程序设计和开发的一个重要方面。 若索引太多, 应用程序的性能可能会受到影响。 而索引太少, 对查询性能又会产生影响。 要找到一个合适的平衡点, 这对应用程序的性能至关重要。
InnoDB 存储引擎支持以下几种常见的索引: B+树索引、 全文索引、 哈希索引, 其中比较关键的是 B+树索引, 其他的索引我们也会在本课程中穿插讲解。
HashMap 适合做数据库索引吗?
- hash 表只能匹配是否相等, 不能实现范围查找;
- 当需要按照索引进行 order by 时, hash 值没办法支持排序;
- 组合索引可以支持部分索引查询, 如(a,b,c)的组合索引, 查询中只用到了a和 b 也可以查询的, 如果使用 hash 表, 组合索引会将几个字段合并 hash, 没办法支持部分索引
- 当数据量很大时, hash 冲突的概率也会非常大。
1. B+Tree
B+树索引就是传统意义上的索引, 这是目前关系型数据库系统中查找最常用 和最为有效的索引。 B+树索引的构造类似于二叉树, 根据键值(Key Value) 快速 找到数据。 注意 B+树中的 B 不是代表二叉(binary), 而是代表平衡(balance), 因 为 B+树是从最早的平衡二叉树演化而来, 但是 B+树不是一个二叉树。
在了解 B+树索引之前先要知道与之密切相关的一些算法与数据结构, 这有 助于我们更好的理解 B+树索引的工作方式, 因为 B+树是通过二叉查找树, 再由 平衡二叉树, B 树演化而来。
- 二分查找
二分查找法(binary search) 也称为折半查找法, 用来查找一组有序的记录 数组中的某一记录。
其基本思想是: 将记录按有序化(递增或递减) 排列, 在查找过程中采用跳 跃式方式查找, 即先以有序数列的中点位置作为比较对象, 如果要找的元素值小 于该中点元素, 则将待查序列缩小为左半部分, 否则为右半部分。 通过一次比较, 将查找区间缩小一半。
给出一个例子, 注意该例子已经是升序排序的, 且查找 数字 48
数据: 5, 10, 19, 21, 31, 37, 42, 48, 50, 52
下标: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
? 步骤一: 设 low 为下标最小值 0 , high 为下标最大值 9 ;
? 步骤二: 通过 low 和 high 得到 mid , mid=(low + high) / 2, 初始时mid 为下标 4 (也可以=5, 看具体算法实现);
? 步骤三 : mid=4 对应的数据值是 31, 31 < 48(我们要找的数字) ;
? 步骤四: 通过二分查找的思路, 将 low 设置为 31 对应的下标 4 , high保持不变为 9 , 此时 mid 为 6 ;
? 步骤五 : mid=6 对应的数据值是 42, 42 < 48(我们要找的数字) ;
? 步骤六: 通过二分查找的思路, 将 low 设置为 42 对应的下标 6 , high保持不变为 9 , 此时 mid 为 7 ;
? 步骤七 : mid=7 对应的数据值是 48, 48 == 48(我们要找的数字) , 查找结束;
通过 3 次二分查找 就找到了我们所要的数字, 而顺序查找需 8 次。
因此二分查找法的效率比顺序查找法要好(平均地来说)。 但如果说查 5 这 条记录, 顺序查找只需 1 次, 而二分查找法需要 4 次。 我们来看, 对于上面 10 个数来说, 顺序查找平均查找次数为(1+2+3+4+5+6+7+8+9+10)/10=5.5 次。 而二 分查找法为(4+3+2+4+3+1+4+3+2+3)/10=2.9 次。 在最坏的情况下, 顺序查找的次 数为 10, 而二分查找的次数为 4。
- 二叉树系列
根据数组的特性我们知道, 有最优的查找效率和空间需求; 能够进行有序性相关操作, 缺点也很明显, 插入和删除操作很慢, 所以为了结合链表插入的灵活性和有序数组查找的高效性, 我们引入了二叉查找树。 那么首先来看看什么是二叉树。 注意, 本节课不是数据结构和算法的专门课, 所以对牵涉到的数据结构和算法不会深入讲解, 只讲解我们可能用到的部分。
二叉树
每个节点至多只有二棵子树, 左子树和右子树, 次序不能颠倒。 逻辑上二叉树有五种基本形态: 空二叉树、 只有一个根结点的二叉树、 只有左子树、 只有右 子树、 完全二叉树(特例为满二叉树) 。 遍历是对树的一种最基本的运算, 所谓遍历二叉树, 就是按一定的规则和顺序走遍二叉树的所有结点, 使每一个结点都被访问一次, 而且只被访问一次, 有前序、 中序、 后序遍历。
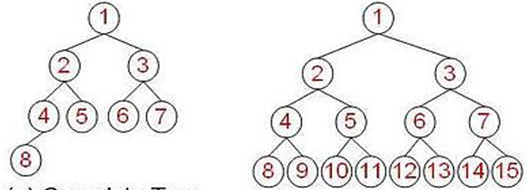
二叉查找(搜索)树
二叉查找树首先肯定是个二叉树, 除此之外, 还规定, 在二叉查找树中, 左 子树的节点值总是小于根的节点值, 右子树的节点值总是大于根的节点值, 也就 是左子树节点值<根的节点值<右子树节点值。 因此可以通过中序遍历得到节点值 的排序输出。 以一个排序好的数组为例:
10、 25、 34、 48、 61、 73、 81
可以将这个数组转为二叉树结构, 其中数组的中间元素作为树的根节点, 左半部分的中间元素作为根节点的左孩子, 右半部分的中间元素作为根节点的右孩 子, 第二层的节点以此类推, 最后树的层数就会越来越多, 这样我们就构建好了 一颗二叉树。
同时这棵树, 对于每个节点而言, 其左孩子都小于它的父节点, 右孩子都大于等于它的父节点。 所以我们把这样的二叉树也是一个二叉查找树(binary search tree) , 它的查找时间复杂度和二分查找一样, O(logN)。
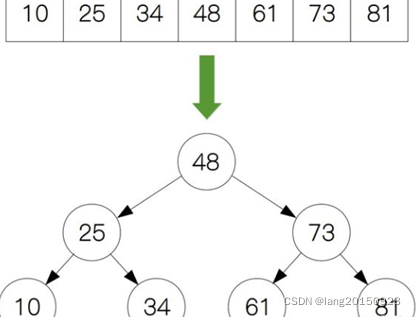
但是二叉查找树, 如果设计不良, 完全可以变成一颗极不平衡的二叉查找树:
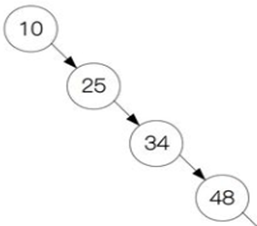
查找效率和顺序查找基本没差别了。 因此若想最大性能地构造一棵二叉查找树, 需要这棵二叉查找树是平衡的, 从而引出了新的定义——平衡二叉树, 或称为 AVL 树。
平衡二叉树(AVL-树)
平衡二叉树的定义如下:首先符合二叉查找树的定义, 其次必须满足任何 节点的两个子树的高度最大差为 1。
平衡二叉树的查找性能是比较高的, 但不是最高的, 只是接近最高性能。 最好的性能需要建立一棵最优二叉树, 但是最优二叉树的建立和维护需要大量的操作, 因此, 用户一般只需建立一棵平衡二叉树即可。
平衡二叉树的查询速度的确很快, 但是维护一棵平衡二叉树的代价是非常大 的。 通常来说, 需要 1 次或多次左旋和右旋来得到插入、 更新和删除后树的平衡性。
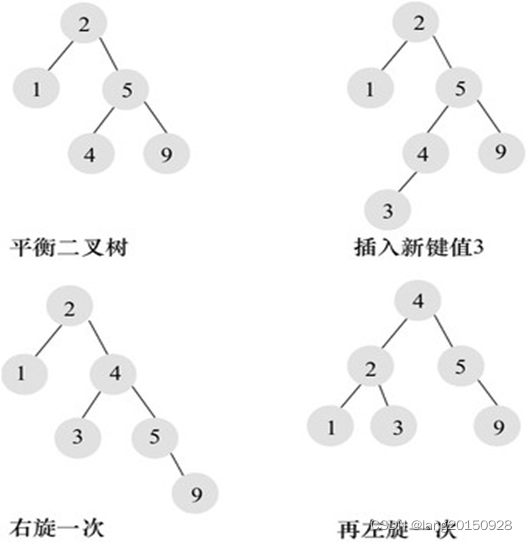
平衡二叉树对一个数据库来说, 有什么问题? 因为二叉树每个节点最多只有 两个直属子节点, 所以当节点数比较多时, 二叉树的高度增长很快, 比如 1000 个节点时, 树的高度差不多有 9 到 10 层。 我们知道数据库是持久化的, 数据是 要从磁盘上读取的, 一般的机械磁盘每秒至少可以做 100 次 IO, 一次 IO 的时间 基本上在 0.01 秒, 1000 个节点在查找时就需要 0.1 秒, 如果是 10000 个节点, ,100000 个节点呢? 所以对数据库来说, 为了减少树的高度, 提出了 B+树的数据 结构。
- B+树
B+树和二叉树、 平衡二叉树一样, 都是经典的数据结构。 B+树由 B 树和索 引顺序访问方法演化而来, 但是在现实使用过程中几乎已经没有使用 B 树的情况 了。
B+树的定义在很多数据结构书中都能找到, 非常复杂, 我们概略它的定义:
B+树是 B 树的一种变形形式, B+树上的叶子结点存储关键字以及相应记录 的地址, 叶子结点以上各层作为索引使用。 一棵 m 阶的 B+树定义如下:
? 每个节点最多可以有 m 个元素;
? 除了根节点外, 每个节点最少有 (m/2) 个元素;
? 如果根节点不是叶节点, 那么它最少有 2 个孩子节点;
? 所有的叶子节点都在同一层;
? 一个有 k 个孩子节点的非叶子节点有 (k-1) 个元素, 按升序排列;
? 某个元素的左子树中的元素都比它小, 右子树的元素都大于或等于它;
? 非叶子节点只存放关键字和指向下一个孩子节点的索引, 记录只存放在
叶子节点中;
? 相邻的叶子节点之间用指针相连。
B+树的变体为 B树, 在 B+树的非根和非叶子结点再增加指向兄弟的指针;B树定义了非叶子结点关键字个数至少为(2/3)*M, 即块的最低使用率为 2/3( 代替 B+树的 1/2) 。
我们概要的了解下 B 树和 B+树
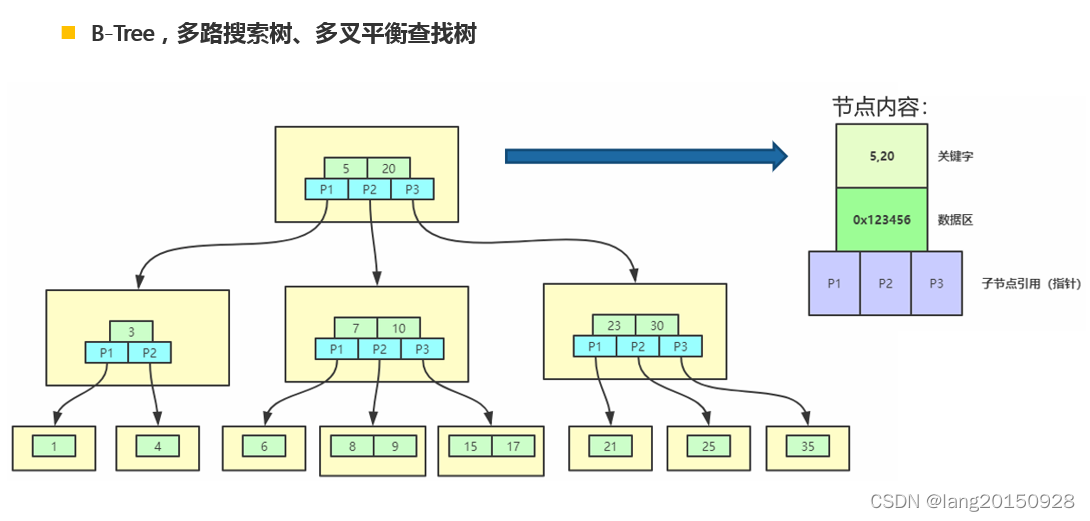
B+树是为磁盘或其他直接存取辅助设备设计的一种平衡查找树。 在 B+树中, 所有记录节点都是按键值的大小顺序存放在同一层的叶子节点上, 由各叶子节点 指针进行连接。 比如:
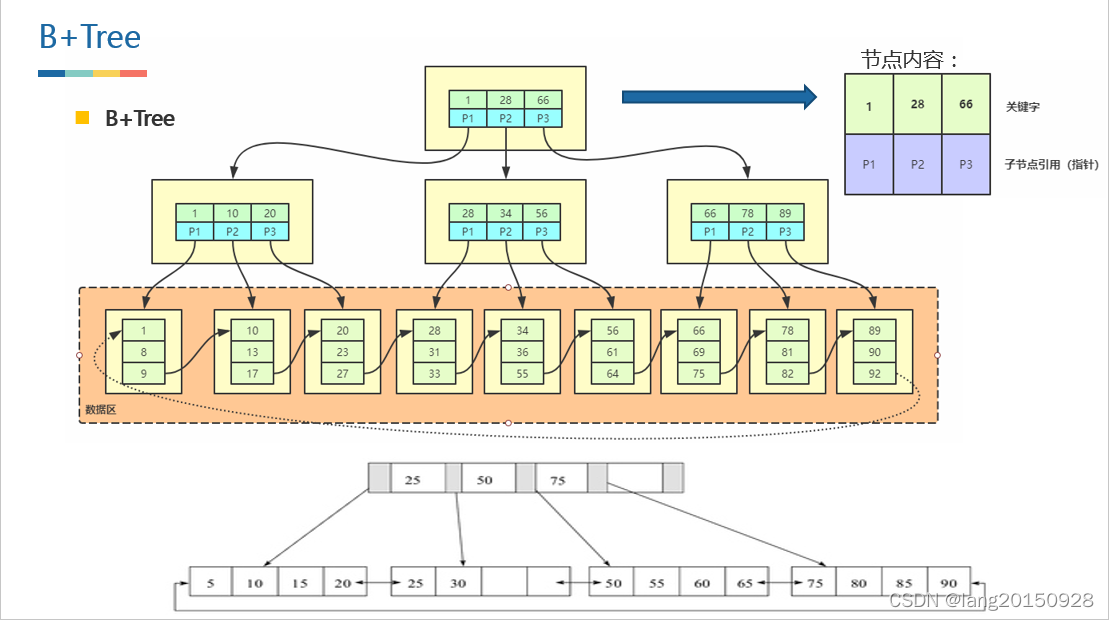
从上图我们可以归纳出 B+树的几个特征, 在 B+树的简要定义中其实已经包
括了:
1、 相同节点数量的情况下, B+树高度远低于平衡二叉树;
2、 非叶子节点只保存索引信息和下一层节点的指针信息, 不保存实际数据记录;
3、 每个叶子页(LeafPage) 存储了实际的数据, 比如上图中每个叶子页就存放了 4 条数据记录, 当然可以更多, 叶子节点由小到大(有序) 串联在一起,叶子页中的数据也是排好序的;
4、 索引节点指示该节点的左子树比这个索引值小, 而右子树大于等于这个索引值。
注意: 叶子节点中的数据在物理存储上完全可以是无序的, 仅仅是在逻辑上有序(通过指针串在一起)。
2. InnoDB 中的索引
聚集索引/聚簇索引
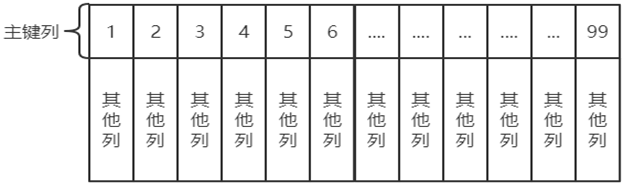
InnoDB中使用了聚集索引,就是将表的主键用来构造一棵B+树,并且将整张表的行记录数据存放在该B+树的叶子节点中。也就是所谓的索引即数据,数据即索引。由于聚集索引是利用表的主键构建的,所以每张表只能拥有一个聚集索引。
聚集索引的叶子节点就是数据页。换句话说,数据页上存放的是完整的每行记录。因此聚集索引的一个优点就是:通过过聚集索引能获取完整的整行数据。另一个优点是:对于主键的排序查找和范围查找速度非常快。
如果我们没有定义主键呢?MySQL会使用唯一性索引,没有唯一性索引,MySQL也会创建一个隐含列RowID来做主键,然后用这个主键来建立聚集索引。
辅助索引/二级索引
上边介绍的聚簇索引只能在搜索条件是主键值时才能发挥作用,因为B+树中的数据都是按照主键进行排序的,那如果我们想以别的列作为搜索条件怎么办?我们一般会建立多个索引,这些索引被称为辅助索引/二级索引。
对于辅助索引(SecondaryIndex,也称二级索引、非聚集索引),叶子节点并不包含行记录的全部数据。叶子节点除了包含键值以外,每个叶子节点中的索引行中还包含了一个书签(bookmark)。该书签用来告诉InnoDB存储引擎哪里可以找到与索引相对应的行数据。因此InnoDB存储引擎的辅助索引的书签就是相应行数据的聚集索引键。
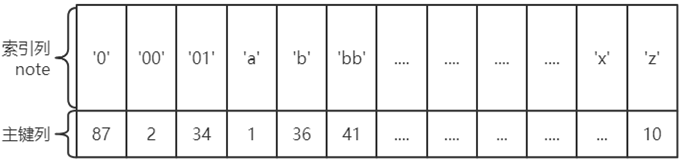
比如辅助索引 index(node), 那么叶子节点中包含的数据就包括了(主键、note)。
回表
辅助索引的存在并不影响数据在聚集索引中的组织,因此每张表上可以有多个辅助索引。当通过辅助索引来寻找数据时,InnoDB存储引擎会遍历辅助索引并通过叶级别的指针获得指向主键索引的主键,然后再通过主键索引(聚集索引)来找到一个完整的行记录。这个过程也被称为回表。也就是根据辅助索引的值查询一条完整的用户记录需要使用到2棵B+树----一次辅助索引,一次聚集索引。
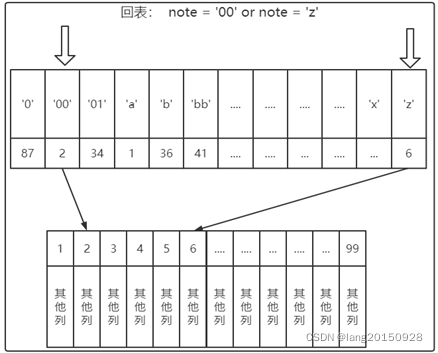
为什么我们还需要一次回表操作呢?直接把完整的用户记录放到辅助索引d的叶子节点不就好了么?如果把完整的用户记录放到叶子节点是可以不用回表,但是太占地方了,相当于每建立一棵B+树都需要把所有的用户记录再都拷贝一遍,这就有点太浪费存储空间了。而且每次对数据的变化要在所有包含数据的索引中全部都修改一次,性能也非常低下。
很明显,回表的记录越少,性能提升就越高,需要回表的记录越多,使用二级索引的性能就越低,甚至让某些查询宁愿使用全表扫描也不使用二级索引。
那什么时候采用全表扫描的方式,什么时候使用采用二级索引+回表的方式去执行查询呢?这个就是查询优化器做的工作,查询优化器会事先对表中的记录计算一些统计数据,然后再利用这些统计数据根据查询的条件来计算一下需要回表的记录数,需要回表的记录数越多,就越倾向于使用全表扫描,反之倾向于使用二级索引+回表的方式。具体怎么算的,我们后面会详细说到。
联合索引/复合索引
前面我们对索引的描述,隐含了一个条件,那就是构建索引的字段只有一个,但实践工作中构建索引的完全可以是多个字段。所以,将表上的多个列组合起来进行索引我们称之为联合索引或者复合索引,比如index(a,b)就是将a,b两个列组合起来构成一个索引。
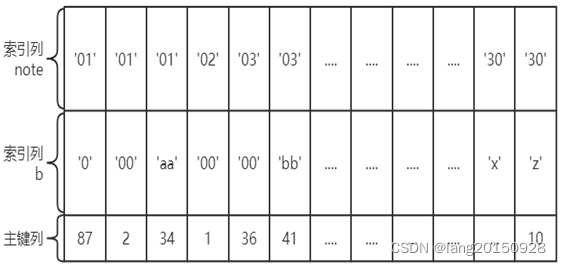
千万要注意一点,建立联合索引只会建立1棵B+树,多个列分别建立索引会分别以每个列则建立B+树,有几个列就有几个B+树,比如,index(note)、index(b),就分别对note,b两个列各构建了一个索引。
index(note,b)在索引构建上, 包含了两个意思:
1、 先把各个记录按照 note 列进行排序。
2、 在记录的 note 列相同的情况下, 采用 b 列进行排序
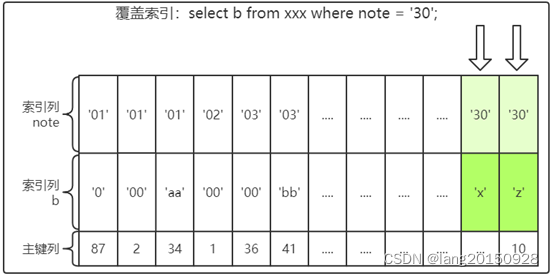
覆盖索引/索引覆盖
既然多个列可以组合起来构建为联合索引, 那么辅助索引自然也可以由多个列组成。
InnoDB存储引擎支持覆盖索引(coveringindex,或称索引覆盖),即从辅助索引中就可以得到查询的记录,而不需要查询聚集索引中的记录。使用覆盖索引的一个好处是辅助索引不包含整行记录的所有信息,故其大小要远小于聚集索引,因此可以减少大量的IO操作。所以记住,覆盖索引并不是索引类型的一种。
InnoDB存储引擎除了我们前面所说的各种索引,还有一种自适应哈希索引,我们知道B+树的查找次数,取决于B+树的高度,在生产环境中,B+树的高度一般为3 ~ 4层,故需要3 ~ 4次的IO查询。
所以在InnoDB存储引擎内部自己去监控索引表,如果监控到某个索引经常用,那么就认为是热数据,然后内部自己创建一个hash索引,称之为自适应哈希索引(AdaptiveHashIndex,AHI),创建以后,如果下次又查询到这个索引,那么直接通过hash算法推导出记录的地址,直接一次就能查到数据,比重复去B+tree索引中查询三四次节点的效率高了不少。
InnoDB存储引擎使用的哈希函数采用除法散列方式,其冲突机制采用链表方式。注意,对于自适应哈希索引仅是数据库自身创建并使用的,我们并不能对其进行干预。通过命令
show engine innodb status\G
可以看到当前自适应哈希索引的使用状况,如
mysql> show engine innodb status\G
*************************** 1. row ***************************
Type: InnoDB
Name:
Status:
=====================================
2022-01-02 14:10:57 0x7fbfd406d700 INNODB MONITOR OUTPUT
=====================================
Per second averages calculated from the last 59 seconds
-----------------
BACKGROUND THREAD
-----------------
srv_master_thread loops: 54 srv_active, 0 srv_shutdown, 127839 srv_idle
srv_master_thread log flush and writes: 127893
----------
SEMAPHORES
----------
OS WAIT ARRAY INFO: reservation count 57
OS WAIT ARRAY INFO: signal count 51
RW-shared spins 0, rounds 91, OS waits 45
RW-excl spins 0, rounds 287, OS waits 0
RW-sx spins 2, rounds 31, OS waits 1
Spin rounds per wait: 91.00 RW-shared, 287.00 RW-excl, 15.50 RW-sx
------------
TRANSACTIONS
------------
Trx id counter 1983
Purge done for trx's n:o < 1980 undo n:o < 0 state: running but idle
History list length 0
LIST OF TRANSACTIONS FOR EACH SESSION:
---TRANSACTION 421936872523616, not started
0 lock struct(s), heap size 1136, 0 row lock(s)
--------
FILE I/O
--------
I/O thread 0 state: waiting for completed aio requests (insert buffer thread)
I/O thread 1 state: waiting for completed aio requests (log thread)
I/O thread 2 state: waiting for completed aio requests (read thread)
I/O thread 3 state: waiting for completed aio requests (read thread)
I/O thread 4 state: waiting for completed aio requests (read thread)
I/O thread 5 state: waiting for completed aio requests (read thread)
I/O thread 6 state: waiting for completed aio requests (write thread)
I/O thread 7 state: waiting for completed aio requests (write thread)
I/O thread 8 state: waiting for completed aio requests (write thread)
I/O thread 9 state: waiting for completed aio requests (write thread)
Pending normal aio reads: [0, 0, 0, 0] , aio writes: [0, 0, 0, 0] ,
ibuf aio reads:, log i/o's:, sync i/o's:
Pending flushes (fsync) log: 0; buffer pool: 0
485 OS file reads, 1833 OS file writes, 623 OS fsyncs
0.00 reads/s, 0 avg bytes/read, 0.00 writes/s, 0.00 fsyncs/s
-------------------------------------
INSERT BUFFER AND ADAPTIVE HASH INDEX
-------------------------------------
Ibuf: size 1, free list len 0, seg size 2, 0 merges
merged operations:
insert 0, delete mark 0, delete 0
discarded operations:
insert 0, delete mark 0, delete 0
Hash table size 34679, node heap has 2 buffer(s)
Hash table size 34679, node heap has 8 buffer(s)
Hash table size 34679, node heap has 3 buffer(s)
Hash table size 34679, node heap has 9 buffer(s)
Hash table size 34679, node heap has 3 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
0.00 hash searches/s, 0.00 non-hash searches/s
---
LOG
---
Log sequence number 20748596
Log flushed up to 20748596
Pages flushed up to 20748596
Last checkpoint at 20748587
0 pending log flushes, 0 pending chkp writes
185 log i/o's done, 0.00 log i/o's/second
----------------------
BUFFER POOL AND MEMORY
----------------------
Total large memory allocated 137428992
Dictionary memory allocated 344815
Buffer pool size 8192
Free buffers 7061
Database pages 1103
Old database pages 414
Modified db pages 0
Pending reads 0
Pending writes: LRU 0, flush list 0, single page 0
Pages made young 0, not young 0
0.00 youngs/s, 0.00 non-youngs/s
Pages read 452, created 651, written 1285
0.00 reads/s, 0.00 creates/s, 0.00 writes/s
No buffer pool page gets since the last printout
Pages read ahead 0.00/s, evicted without access 0.00/s, Random read ahead 0.00/s
LRU len: 1103, unzip_LRU len: 0
I/O sum[0]:cur[0], unzip sum[0]:cur[0]
--------------
ROW OPERATIONS
--------------
0 queries inside InnoDB, 0 queries in queue
0 read views open inside InnoDB
Process ID=1, Main thread ID=140461452809984, state: sleeping
Number of rows inserted 64715, updated 0, deleted 0, read 121011
0.00 inserts/s, 0.00 updates/s, 0.00 deletes/s, 0.00 reads/s
----------------------------
END OF INNODB MONITOR OUTPUT
============================
1 row in set (0.00 sec)
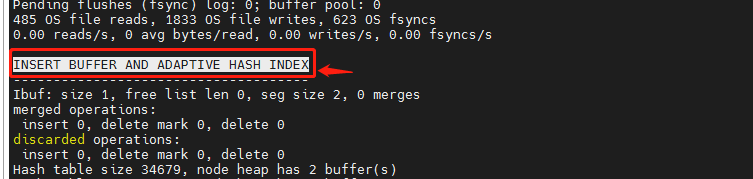
哈希索引只能用来搜索等值的查询,如 SELECT* FROM table WHERE index co=xxx。 而对于其他查找类型,如范围查找,是不能使用哈希索引的,
因此这里出现了 non- hash searches/s 的情况。 通过 hash searches: nonhash searches 可以大概了解使用哈希索引后的效率。
由于 AHI 是由 InnoDB 存储引擎控制的,因此这里的信息只供我们参考。 不过我们可以通过观察 SHOW ENGINE INNODB STATUS 的结果及参数innodb_adaptive_hash_index 来考虑是禁用或启动此特性,默认 AHI 为开启状态。
什么时候需要禁用呢? 如果发现监视索引查找和维护哈希索引结构的额外开销远远超过了自适应哈希索引带来的性能提升就需要关闭这个功能。
同时在 MySQL 5.7 中, 自适应哈希索引搜索系统被分区。 每个索引都绑定到一个特定的分区, 每个分区都由一个单独的 latch 锁保护。 分区由innodb_adaptive_hash_index_parts 配置选项控制 。 在早期版本中, 自适应哈希索引搜索系统受到单个 latch 锁的保护, 这可能成为繁重工作负载下的争用点。 innodb_adaptive_hash_index_parts 默认情况下, 该 选项设置为 8。 最大
设置为 512。 当然禁用或启动此特性和调整分区个数这个应该是 DBA 的工作, 我们了解即可。
3. 创建和删除索引的语句
那我们如何使用 SQL 语句去建立这种索引呢? InnoDB 和 MyISAM 会自动为主键或者声明为 UNIQUE 的列去自动建立 B+树索引, 但是如果我们想为其他的列建立索引就需要我们显式的去指明。 为啥不自动为每个列都建立个索引呢?我们待会说。
查看索引
SHOW INDEX FROM table_name\G
创建修改索引
CREATE TALBE 表名 (
各种列的信息 · · · ,
[KEY|INDEX] 索引名 (需要被索引的单个列或多个列)
)
CREATE [UNIQUE ] INDEX indexName ON mytable(columnname(length));
ALTER TABLE 表名 ADD [UNIQUE ] INDEX [indexName] ON (columnname(length))
删除索引
DROP INDEX [indexName] ON mytable;
ALTER TABLE 表名 DROP [INDEX|KEY] 索引名
4. 索引的代价
世界上从来没有只有好处没有坏处的东西, 如果你有, 请你一定要告诉我,让我也感受一下。 虽然索引是个好东西, 在学习如何更好的使用索引之前先要了解一下使用它的代价, 它在空间和时间上都会拖后腿。
空间上的代价
这个是显而易见的, 每建立一个索引都要为它建立一棵 B+树, 每一棵 B+树的每一个节点都是一个数据页, 一个页默认会占用 16KB 的存储空间, 一棵很大的 B+树由许多数据页组成会占据很多的存储空间。
时间上的代价
每次对表中的数据进行增、删、改操作时,都需要去修改各个B+树索引。而且我们讲过,B+树每层节点都是按照索引列的值从小到大的顺序排序而组成了双向链表。不论是叶子节点中的记录,还是非叶子内节点中的记录都是按照索引列的值从小到大的顺序而形成了一个单向链表。
而增、删、改操作可能会对节点和记录的排序造成破坏,所以存储引擎需要额外的时间进行一些记录移位,页面分裂、页面回收的操作来维护好节点和记录的排序。如果我们建了许多索引,每个索引对应的B+树都要进行相关的维护操作,这必然会对性能造成影响。
既然索引这么有用,我们是不是创建越多越好?既然索引有代价,我们还是别创建了吧?当然不是!那么我们应该怎么创建索引呢?参考后续:高性能的索引创建策略