01背包问题
有n件物品和一个最大容量为w的背包。第i件物品的重量为weight[i],对应的价值为value[i]。每件物品只能选取一次,问如何选取物品能使背包中物品的总价值达到最大?
二维dp
动态规划的做法是,借助一个n行,w + 1列的二位数组dp,其中dp[i][j]表示在[0,i]的物品中选取,放进容量为j的背包时能达到的最大价值
接下来考虑如何得到dp[i][j]:此时背包的容量为j,那么对于第i件物品,当它的重量weight[i]大于j时,显然它怎么样都放不进背包,也就是说此时我们只能选取[0,i - 1]的物品,也即使用选取[0,i - 1]时得到的最大价值。那么dp[i][j] = dp[i - 1][j];如果weight[i]小于等于j,第i件物品是可以放入背包的,那么就要考虑要不要放进去,并不一定放进去能带来更大的收益。不放的话跟前面一样dp[i][j] = dp[i - 1][j],放的话,第i件物品就占据了背包容量j中weight[i]的容量,那么剩下的j - weight[i]的部分就要在[0,i]的物品选取了,所以此时dp[i][j] = dp[i - 1][j - weight[i]] + value[i]。所以当weight[i - 1]小于等于j时,dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - weight[i]] + value[i])
边界就是第0行和第0列:第0行表示只能选择物品0时能得到的最大价值,所以当j>=weight[0]时,dp[0][j] = value[0];否则dp[0][j] = 0;第0列表示选取物品放入容量为0的背包能得到的最大价值,显然容量为0能得到的价值都是0
代码:
public static int ZeroOneBag(int[] weight, int[] value, int w){
int n = weight.length;
//为了和value数组和weight数组对齐,下标0表示第一件物品,所以数组为n行
int[][] dp = new int[n][w + 1];
//初始化边界
for (int i = 0;i < n;i++){
dp[i][0] = 0;
}
for(int i = weight[0];i <= w;i++){
dp[0][i] = value[0];
}
//根据状态转移方程得到每个状态,这里的推导方向是 从左到右,从上到下
//外层循环为物品,内层循环为背包容量
for (int i = 1;i < n;i++){
for (int j = 1;j <= w;j++){
if (j < weight[i]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - weight[i]] + value[i]);
}
}
}
return dp[n - 1][w];
}
由状态转移方程可以知道,dp[i][j]的值来自于上一行中列数小于等于j的元素:
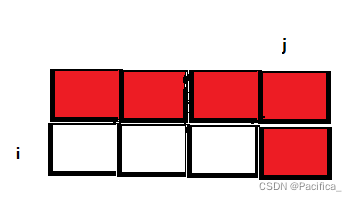
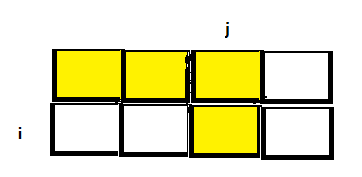
所以状态推导过程改为外层循环为背包容量,内层循环为物品(先从上到下,再从左到右)也是可以的
一维dp
借助动态规划解题,时间复杂度貌似没有可以改进的地方了,但空间复杂度可以改进
根据上面代码中外层循环为物品,内层循环为背包容量的推导过程可以发现,二维数组中每一行的数据都来自于上一行的数据,所以可以把最后一行看成是由第一行这个一维数组经过n - 1次循环覆盖值得到的
只需使用一个大小为w + 1的数组,初始状态是只有第一件物品可以选取时能得到的最大价值,也就是二维数组中的第一行。然后进行n - 1次循环,每次表示多了一件物品可以选取,每一次循环的状态方程就是dp[j] = max(dp[j],dp[j - weight[i]] + value[i]),其中i表示循环的序号,也就是物品的序号
要注意的地方是,根据二维数组中的推导过程可以知道,每开始新的一次循环时,一维数组中每一个数组元素的值来自它左边的数组元素在上一次循环结束时得到的值,所以如果还是像二维数组中一样从左到右推导的话,计算右边的数组元素值时会得到错误的答案,所以应该从右往左推导
public static int ZeroOneBagImprove(int[] weight, int[] value, int w){
int n = weight.length;
int[] dp = new int[w + 1];
//因为是一维数组,所以不用考虑边界
//外层循环为物品,内层循环为背包容量
for (int i = 0;i < n;i++){
for (int j = w;j >= 1;j--){
if (j < weight[i]){
dp[j] = dp[j];
}else{
dp[j] = Math.max(dp[j],dp[j - weight[i]] + value[i]);
}
}
}
return dp[w];
}
完全背包
与01背包不同的地方在于,完全背包中,每一件物品可以选取任意次
这种情况下,考虑从[0,i]的物品中选取,能使背包容量达到最大价值的做法,即二维01背包中的dp[i][j]:如果j小于weight[i],此时无法选取第i件物品,dp[i][j]=dp[i - 1][j];如果j大于等于weight[i],那么考虑不选还是选能带来更大的收益,选的话,剩下的j - weight[i]的部分与01背包不同,可以有第i件物品的参与,所以dp[i][j]可能是dp[i][j - weight[i]] + value[i](这也是后面代码中在循环背包容量时要从左往右遍历的原因) 也可能是 dp[i - 1][j - weight[i]] + value[i],不选的话,就是 dp[i - 1][j],只需要取这些值中的最大值
看起来要考虑的情况好像很多,dp[i][j]的值需要根据第i行以及第i - 1行中列数小于等于j的元素值来得到的
其实只需要在01背包的代码上做一点修改就可以(这里直接使用了一维数组的版本):
public static int CompleteBag(int[] weight, int[] value, int w){
int n = weight.length;
int[] dp = new int[w + 1];
for (int i = 0;i < n;i++){
//只需修改下面这个循环的遍历顺序
for (int j = 1;j <= w;j++){
if (j >= weight[i]){
dp[j] = Math.max(dp[j],dp[j - weight[i]] + value[i]);
}
}
}
return dp[w];
}
与一维的01背包大致一样,外循环是从上到下遍历物品,而这里的内循环是从左到右进行dp值的计算,这样做恰能考虑到前面说到的各种情况。由于遍历背包容量的时候是从左到右的,所以dp[j - weight[i]] + value[i]是包含了dp[i - 1][j - weight[i]] + value[i]的贡献的