题目
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
解题思路
基于归并排序,首先要对归并排序很熟悉
void Merge(int arr[], int l, int q, int r) {
int n = r - l + 1;//临时数组存合并后的有序序列
int* tmp = new int[n];
int i = 0;
int left = l;
int right = q + 1;
while (left <= q && right <= r)
tmp[i++] = arr[left] <= arr[right] ? arr[left++] : arr[right++];
while (left <= q)
tmp[i++] = arr[left++];
while (right <= r)
tmp[i++] = arr[right++];
for (int j = 0; j < n; ++j)
arr[l + j] = tmp[j];
delete[] tmp;//删掉堆区的内存
}
void MergeSort(int arr[], int l, int r) {
if (l == r)
return; //递归基是让数组中的每个数单独成为长度为1的区间
int q = (l + r) / 2;
MergeSort(arr, l, q);
MergeSort(arr, q + 1, r);
Merge(arr, l, q, r);
}
我们以数组{7,5,6,4}为例来分析统计逆序对的过程:
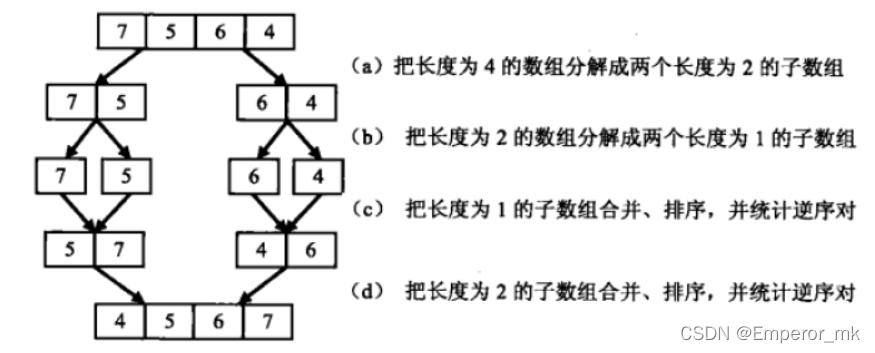
先把数组分解成两个长度为2的子数组,再把这两个子数组分解成两个长度为1的子数组。接下来一边合并相邻的子数组,一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7>5,因此(7,5)组成一个逆序对。同样在第二对长度为1的子数组{6},{4}中也有逆序对(6,4),由于已经统计了这两对子数组内部的逆序对,因此需要把这两对子数组进行排序,避免在之后的统计过程中重复统计。
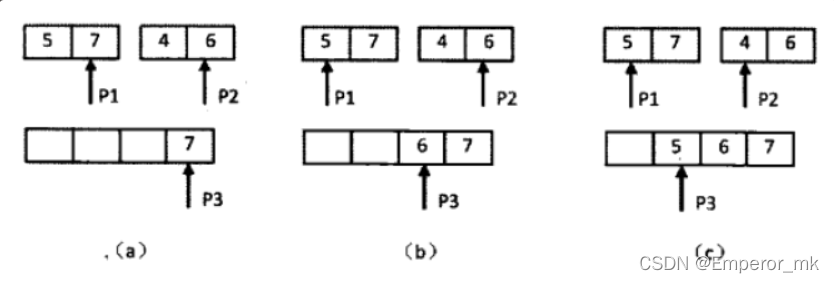
逆序对的总数 = 左边数组中的逆序对的数量 + 右边数组中逆序对的数量 + 左右结合成新的顺序数组时中出现的逆序对的数量
总结一下:
这是一个归并排序的合并过程,主要是考虑合并两个有序序列时,计算逆序对数。
对于两个升序序列,设置两个下标:两个有序序列的末尾。每次比较两个末尾值,如果前末尾大于后末尾值,则有”后序列当前长度“个逆序对;否则不构成逆序对。然后把较大值拷贝到辅助数组的末尾,即最终要将两个有序序列合并到辅助数组并有序。
这样,每次在合并前,先递归地处理左半段、右半段,则左、右半段有序,且左右半段的逆序对数可得到,再计算左右半段合并时逆序对的个数。
C++实现
class Solution
{
public:
int InversePairs(int *data, int length)
{
if (data == nullptr || length < 0)
return 0;
int *copy = new int[length];
for (int i = 0; i < length; ++i)
copy[i] = data[i];
int count = InversePairsCore(data, copy, 0, length - 1);
delete[]copy;
return count;
}
int InversePairsCore(int *data, int *copy, int start, int end)
{
if (start == end)
{
copy[start] = data[start];
return 0;
}
int length = (end - start) / 2;
int left = InversePairsCore( copy, data, start, start+length);
int right = InversePairsCore(copy, data, start + length+1,end);
//i初始化为前半段最后一个数字的下标
int i = start + length;
//j初始化为后半段最后一个数字的下标
int j = end;
int indexCopy = end;
int count = 0;
while (i >= start && j >= start + length + 1)
{
if (data[i] > data[j])
{
copy[indexCopy--] = data[i--];
count += j - start - length;
}
else
copy[indexCopy--] = data[j--];
}
for (; i >= start; --i)
copy[indexCopy--] = data[i];
for (; j >= start + length + 1; --j)
copy[indexCopy--] = data[j];
return left + right + count;
}
};
- 时间复杂度:O(nlongn),主要为归并排序的时间消耗
- 空间复杂度:O(n),归并排序需要一个长度为n的辅助数组
注意
之所以交换copy和data的顺序是因为:
首先data=copy,经过排序后data左半部分仍旧乱序,但copy左半部分已经存储了排好序的data左半部分,即已经保存了data左半部分的信息,这样在向上层递归时,data左半部分本身可以作为容器,copy左半部分作为已经排好序的一个单元,即代拍序列的一个元素。