洛谷:矩阵旋转

观察可以发现: できない
对于这样的两列表格,一次 2x2 的正方形 180° 旋转相当于 左上与右下、左下与右上交换
而这样的交换不会改变什么?不会改变任意一列的两个数字!
但会改变这两个数字的位置关系,旋转一次就上下颠倒一次
所以我们得到了第一个判断无解的条件:
若 原状态 任意一列的两个数字在 目标状态 中位置不是在同一列,显然无解
接着,在排除了以上无解情况后,我们又可以 通过看题解 发现:
原状态 任意一列的两个数字在 目标状态 中对应的位置不同,解的存在性也会改变!
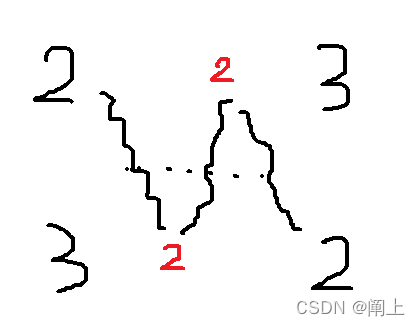
2
/
3
2/3
2/3 要转化成
3
/
2
3/2
3/2 中间旋转的次数显然是 奇数次 !
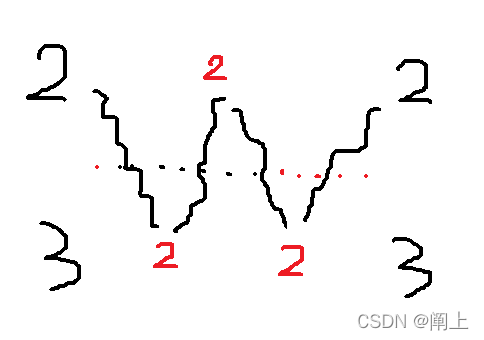
同理,若 原状态 到 目标状态 的列上下关系没变,旋转次数就是 偶数次
若不满足这 奇偶性 ,显然无解
—————————————————————————————————————
综上,我们终于探讨完了有无解的判断
那怎么求 最少 旋转次数呢?
可以观察到,同一列的两个数字怎么旋转都是捆绑在一起的、不会变动,所以可以把 一列 当成 一个数字
这样问题就转化成:
原状态 的一列数字 转化成 目标状态 的一列数字,问转化的最小步数(转化方式是交换任意相邻的两列数字)
通过经验我们可知:在一个序列(由母版映射过来)里求逆序对的数量 == 这个序列从母版转化过来的最小步数
所以,上代码:
#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul (u << 1)
#define ur (u << 1 | 1)
#define fx first
#define fy second
//#pragma GCC optimize(2)
//[博客地址](https://blog.csdn.net/weixin_51797626?t=1)
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1000010, M = 110, MM = 3000010;
int INF = 0x3f3f3f3f, mod = 100003;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
struct arr
{
int row, col;
}ch[N << 1];//开大啊!!!开小了re错误都没直接wa
int b[3][N], z[N], tmp[N];
bool check() {
for (int j = 1; j <= n; j++) {
int b1 = b[1][j], b2 = b[2][j];
if (ch[b1].col != ch[b2].col)return false;
//首先先判 同列 是否合法
}
for (int j = 1; j <= n; j++) {
int b1 = b[1][j];
if (ch[b1].row == 1) { //再判奇偶
if (ch[b1].col % 2 != j % 2)return false;
}
else {
if (ch[b1].col % 2 == j % 2)return false;
}
}
return true;
}
ll gui_sort(int l, int r) {
if (l >= r)return 0;//递归边界勿忘,否则死循环上门服务
int mid = l + r >> 1;
ll cnt = gui_sort(l, mid) + gui_sort(mid + 1, r);
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r)
{
if (z[i] <= z[j])tmp[k++] = z[i++];
else {
//找到第一个 i 大于 j,显然 i 之后的所有数都大于 j,统计到逆序对的数量中
cnt += (ll)mid - i + 1;
tmp[k++] = z[j++];
}
}
while (i <= mid)tmp[k++] = z[i++];
while (j <= r)tmp[k++] = z[j++];
for (int i = l; i <= r; i++)z[i] = tmp[i];
return cnt;
}
int main() {
cinios;
cin >> n;
for (int i = 1; i <= 2; i++)
for (int j = 1; j <= n; j++) {
int t;
cin >> t;
ch[t] = { i,j };//记录母版(原状态)的数所处的行列信息
//题目告诉我们数是不重不漏的
//注意这里的数最多有 2*n 个...数组开小了bug找一天
}
for (int i = 1; i <= 2; i++)
for (int j = 1; j <= n; j++)
cin >> b[i][j];//目标状态
if (!check()) {
cout << "dldsgay!!1";
return 0;
}
for (int j = 1; j <= n; j++)//母版映射过来的序列,用来求逆序对
z[j] = ch[b[2][j]].col;
cout << gui_sort(1, n);
return 0;
}
—————————————————————————————————————
更简便的一种判断方法,摘自洛谷题解

所有数字可以分成两种状态,
W
和
M
W 和 M
W和M
只要有 W 的数字跑到了 M 的位置,或者反之,就可以说明无解
代码:
#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul (u << 1)
#define ur (u << 1 | 1)
#define fx first
#define fy second
//#pragma GCC optimize(2)
//[博客地址](https://blog.csdn.net/weixin_51797626?t=1)
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1000010, M = 110, MM = 3000010;
int INF = 0x3f3f3f3f, mod = 100003;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
int st[N << 1];
int a[N][2], b[N][2], z[N], tmp[N];
ll gui_sort(int l, int r) {
if (l >= r)return 0;//递归边界勿忘
int mid = l + r >> 1;
ll cnt = gui_sort(l, mid) + gui_sort(mid + 1, r);
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r)
{
if (z[i] <= z[j])tmp[k++] = z[i++];
else {
cnt += (ll)mid - i + 1;
tmp[k++] = z[j++];
}
}
while (i <= mid)tmp[k++] = z[i++];
while (j <= r)tmp[k++] = z[j++];
for (int i = l; i <= r; i++)z[i] = tmp[i];
return cnt;
}
int main() {
cinios;
cin >> n;
for (int i = 0; i < 2; i++)
for (int j = 1; j <= n; j++)cin >> a[j][i];//注意 j 在前,i 记录上下状态
for (int i = 0; i < 2; i++)
for (int j = 1; j <= n; j++)cin >> b[j][i];
for (int i = 1; i <= n; i++)
st[a[i][i & 1]] = i;//对原状态记录一下 M 类型在哪个列(记录W也可)
for (int i = 1; i <= n; ++i) {
if (st[b[i][i & 1]])z[i] = st[b[i][i & 1]];//顺手记录序列
//对应在 目标状态 看看这个数字是不是还是 M 类型
//若不是就无解,因为 旋转操作 不可能会让数跑到其他状态上
else {
cout << "dldsgay!!1";
return 0;
}
}
cout << gui_sort(1, n);
return 0;
}
简洁优美