[数据结构与算法]LeetCode面试热题十二

279. 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。
完全平方数是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

• 1 <= n <= 10⁴

方法一：动态规划，dp[i]表示和为 i 时，平方数的最少数量。 动态规划的状态转移方程：
dp[ i ] = min( dp[ i - j*j ] + 1，dp[ i ] )，j 为 1 到 sqrt(i)。

public int numSquares(int n) {
    int[] dp = new int[n+1];
    for(int i = 1; i <= n;i++){
        dp[i] = Integer.MAX_VALUE;
        for(int j = 1; j * j <= i;j++){
            dp[i] = Math.min(dp[i],dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

方法二：利用 四平方和定理。四平方和定理证明了任意一个正整数都可以被表示为至多四个正整数的平方和。这给出了本题的答案的上界。
同时四平方和定理包含了一个更强的结论：当且仅当 n ≠ 4^k (8m+7)时，n 可以被表示为至多三个正整数的平方和。因此，当 n = 4^k (8m+7)时，n 只能被表示为四个正整数的平方和。此时我们可以直接返回 4。
n ≠ 4^k (8m+7) 时，我们需要判断到底多少个完全平方数能够表示 n，我们知道答案只会是 1,2,3 中的一个：
答案为 1 时，则必有 n 为完全平方数，这很好判断；
答案为 2 时，则有 n=a²+b² ，我们只需要枚举所有的 a (1 ≤ a ≤ sqrt(n) ) ，判断 n-a² 是否为完全平方数即可；
答案为 3 时，我们很难在一个优秀的时间复杂度内解决它，但我们只需要检查答案为 1 或 2 的两种情况，即可利用排除法确定答案。

public int numSquares(int n) {
    if (isPerfectSquare(n)) {
        return 1;
    }
    if (checkAnswer4(n)) {
        return 4;
    }
    for (int i = 1; i * i <= n; i++) {
        int j = n - i * i;
        if (isPerfectSquare(j)) {
            return 2;
        }
    }
    return 3;
}
// 判断是否为完全平方数
public boolean isPerfectSquare(int x) {
    int y = (int) Math.sqrt(x);
    return y * y == x;
}
// 判断是否能表示为 4^k*(8m+7)
public boolean checkAnswer4(int x) {
    while (x % 4 == 0) {
        x /= 4;
    }
    return x % 8 == 7;
}

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
示例:

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

• 必须在原数组上操作，不能拷贝额外的数组。
• 尽量减少操作次数。

解题思路：双指针，左指针指向已经处理的数组的尾部，右指针指向正在处理的位置。

public void moveZeroes(int[] nums) {
    int left = 0;
    for(int right = 0;right < nums.length; right++){ 
        if(nums[right] != 0){
        	// 后面不为0的元素，覆盖前面的值。
            nums[left++] = nums[right];
        }
    }
    // 最后补0
    while(left<nums.length){
        nums[left++] = 0;
    }
}

287. 寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ，找出 这个重复的数 。
你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

示例：

输入：nums = [1,3,4,2,2]
输出：2

提示：

• 1 <= n <= 10⁵
• nums.length == n + 1
• 1 <= nums[i] <= n
• nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

**方法一：二分查找。定义cnt[i] 表示 nums 数组中小于等于 i 的数有多少个，如果数字 i 之前的 1 - i 没有重复，则 cnt[i] = i 。如果 i 之前的 1-i之前有数字重复，则cut[i] > i，只需要找到第一个cut[i] > i的数，就是重复的数。 **

public int findDuplicate(int[] nums) {
    int n = nums.length;
    	int left,right,mid,cut,ans = 0;
    	// 从 1 - n-1中找到重复的数。
        left = 1;
        right = n - 1;
        while(left <= right){
       		// 二分查找，每次找到中间的数。
            mid = left + (right-left)/2;
            cut = 0;
            // 统计小于等于mid的数量。
            for(int i = 0;i < n;i++){
                if(nums[i] <= mid){
                    cut++;
                }
            }
            if(cut <= mid){
                left = mid + 1;
            }else{
                right = mid - 1;
                // 记录最终结果，重复的数为，第一个 cut[i] > i 的数
                ans = mid;
            }
        }
        return ans;
    }

方法二：快慢指针，将数组中的数看着指针，如nums[i] = 2，表示指向 nums[2] 的指针，如果数组中的有重复的数，则说明链表中存在环，即有多个指针指向同一个位置。
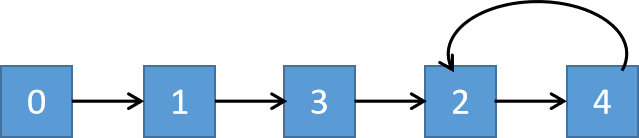
如示例中 nums[1,3,4,2,2] ，将数组中的值与下标，建立关系映射。
0–>1
1–>3
2–>4
3–>2
4–>2
则从 下标 0 开始出发，0–>1–>3–>2–>4–>2–>4… 出现环。环的入口即为重复出现的元素。

算法步骤：
设置慢指针 slow 和快指针 fast，慢指针每次走一步，快指针每次走两步。找到快慢指针相遇的点，然后将慢指针放置到起点。两个指针每次同时移动一步，相遇的点就是环的入口，即为答案。

推导：
设从起点到环的入口的步数是 a。设环长为 L。设从环的入口继续走 b 步到达相遇位置，从相遇位置继续走 c 步回到环的入口，则有 b + c = L，其中 L、a、b、c 都是正整数。
慢指针走了 a + b 步，快指针走了 2(a+b) 步。在相遇位置，快指针比慢指针多走了若干圈，快指针走的步数还可以表示成 a+b+kL，k 表示快指针在环上走的圈数。
2(a+b) = a + b + kL。
解得：a = kL?b = (k?1)L + c
可知，慢指针从起点开始走 a步，到达环的入口，快指针从环中走 c 步，可到达环的入口，两个指针在环的入口相遇，相遇点就是答案。

public int findDuplicate(int[] nums) {     
    int slow = 0, fast = 0;
    do {
        slow = nums[slow];
        fast = nums[nums[fast]];
    } while (slow != fast);
    slow = 0;
    while (slow != fast) {
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
}

289. 生命游戏

根据 百度百科 ，生命游戏，简称为生命，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态：1 即为活细胞（live），或 0 即为死细胞（dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

• 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
• 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
• 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
• 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

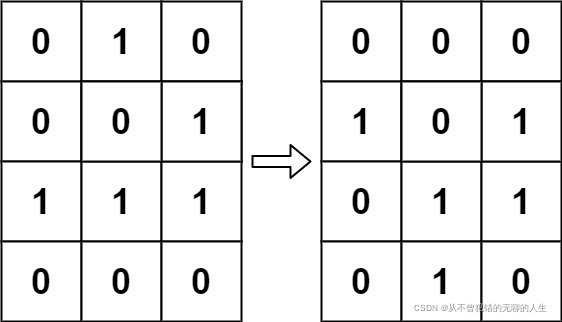
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

解题思路：使用每个数的最低位表示当前细胞的状态，使用每个数的第二位表示下一个状态。求解所有细胞的下一状态后，将所有细胞的状态更新。

public void gameOfLife(int[][] board) {
    // 第一位表示当前状态，使用第二位来表示下一个的状态。
    int m = board.length;
    int n = board[0].length;
    int liveNum;
    for(int i = 0;i < m; i++){
        for(int j = 0;j < n;j++){
            liveNum = 0;
            // 考虑相邻的八个位置
            // [i-1,j-1], [i-1,j],  [i-1,j+1]
            // [i,j-1],   [i,j],    [i,j+1]
            // [i+1,j-1], [i+1,j],  [i+1,j+1]
            int r = i - 1;
            int c = j - 1;
            for(int ri = 0;ri < 3;ri++){
                for(int ci = 0;ci<3;ci++){
                    if(ri == 1 && ci == 1) {
                        continue;
                    }
                    if((r+ri)>=0 && (r+ri) < m && (c+ci) >= 0 && (c+ci) < n 
                    	&& (board[r+ri][c+ci]&1) == 1){
                        liveNum++;
                    }
                }
            }
            // 根据 liveNum 的数量考虑当前细胞的状态。
            if((board[i][j]&1) == 1){
                // 当前为活细胞
                if(liveNum == 2|| liveNum == 3){
                    // 下一个状态活着，第二位置 1
                    board[i][j] = board[i][j]|2;
                }
                // 因为第二位原本就是0，liveNum为其它值时，不用改变第二位状态
            }else{
                // 当前为死细胞
                if(liveNum == 3){
                    // 第二位置1，下一状态是活着。
                    board[i][j] = board[i][j]|2;
                }
            }
        }
    }
    // 更新数组
    for(int i =  0;i < m; i++){
        for(int j = 0;j < n;j++){
            board[i][j] = board[i][j]>>>1;
        }
    }
}

295. 数据流的中位数

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。
例如：[2,3,4] 的中位数是 3、[2,3] 的中位数是 (2 + 3) / 2 = 2.5 。

设计一个支持以下两种操作的数据结构：
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

示例：

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2

进阶:
如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？
如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

解题思路：使用两个优先队列，queueMax，queueMin，分别保存小于中位数的数，大于等于中位数的数。当累计添加的数的数量为奇数时，queMin 中的数的数量比 queMax 多一个，此时中位数为 queMin 的队头。当累计添加的数的数量为偶数时，两个优先队列中的数的数量相同，此时中位数为它们的队头的平均值。

考虑添加一个 num 到数据结构中：

1. num <= queueMin.peek()
   num存入 queueMin，如果 queueMin.size() 大于 queueMax.size() + 1 ，说明 queueMin 中数量太多，则将 queueMin中 的最大节点放入 queueMax中。
2. num > queueMax.peek()
   num存入 queueMax，如果queueMax.size() 大于 queueMin.size()，说明 queueMax数量太多，则将queueMax中的最小节点放入queueMin中。
3. 当 queueMin为空，num添加到queueMin中。

class MedianFinder {
    // 最小堆
    PriorityQueue<Integer> queueMin;
    // 最大堆
    PriorityQueue<Integer> queueMax;
    public MedianFinder() {
        queueMin = new PriorityQueue<>((a,b)->(b-a));
        queueMax = new PriorityQueue<>((a,b)->(a-b));
    }
    public void addNum(int num) {
        if(queueMin.isEmpty() || queueMin.peek() >= num){
            // 添加到 queueMin中
            queueMin.offer(num);
            if(queueMin.size() > queueMax.size() + 1){
            	//将queueMin.peek(),放入queueMax中。
                queueMax.offer(queueMin.poll());
            }
        }else{
            // 添加到 queueMax中
            queueMax.offer(num);
            if(queueMin.size() < queueMax.size()){
            	// 将queueMax.peek()，放入 queueMin中。
                queueMin.offer(queueMax.poll());
            }
        }
    }
    public double findMedian() {
        // 奇数个，queueMin.peek()就是中位数
        if(queueMin.size() > queueMax.size()){
            return queueMin.peek();
        }
        return (queueMax.peek() + queueMin.peek())/2.0;
    }
}

297. 二叉树的序列化与反序列化

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

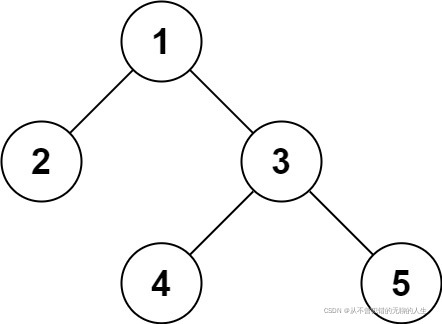
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

提示：

• 树中结点数在范围 [0, 104] 内
• -1000 <= Node.val <= 1000

解题思路：使用层次遍历对树进行序列号和反序列。null 节点，序列化为字符 “n”。在反序列化的时候进行识别。

class Codec {

    public String serialize(TreeNode root) {
        StringBuffer sb = new StringBuffer();
        TreeNode node;
        int size;
        // 层次偏历
        Deque<TreeNode> deque = new LinkedList<>();
        deque.add(root);
        while(!deque.isEmpty()){
            size = deque.size();
            // 序列化
            for(int i = 0;i < size;i++){
                node = deque.poll();
                if(node == null){
                	// 如果为null，序列化为 "n"
                    sb.append("n,");
                }else{
                	// 值序列化，将左右节点加入队列。
                    sb.append(String.valueOf(node.val) + ',');
                    deque.offer(node.left);
                    deque.offer(node.right);
                }
            }
        }
        // 将最后一个 "," 去除
        sb.deleteCharAt(sb.length()-1);
        return sb.toString();
    }
 	// 反序列化
    public TreeNode deserialize(String data) {
        String[] s = data.split(",");
        TreeNode root,p;
        Deque<TreeNode> deque = new LinkedList<>();
        int i = 0;
        int size;
        // 如果第一个 是 n，则证明这个树为空。
        if(s[0].equals("n")){
            return null;
        }
        root = new TreeNode(Integer.parseInt(s[i++]));
        deque.offer(root);
        while(!deque.isEmpty()){
            size = deque.size();
            for(int j = 0;j < size; j++){
                p = deque.poll();
                if(!s[i].equals("n")){
                    p.left = new TreeNode(Integer.parseInt(s[i]));
                    deque.offer(p.left);
                }
                i++;
                if(!s[i].equals("n")){
                    p.right = new TreeNode(Integer.parseInt(s[i]));
                    deque.offer(p.right);
                }
                i++;
            }
        }
        return root;
    }
}

300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

解题思路：动态规划，dp[ i ] 为第 i 个结尾的最长严格递增子序列的长度。
dp[i] = Max( dp[0] 到 dp[ i - 1] ) + 1 ( dp[i] > dp[0] 到 dp[i-1] )

public int lengthOfLIS(int[] nums) {
    int n = nums.length;
    int max = 1;
    // 记录以 i 结尾的最长严格递增子序列的长度
    int[] dp = new int[n];
    dp[0] = 1;
    for(int i = 1;i < n;i++){
    	// 初始化为 1
        dp[i] = 1;
        // 考虑前面的每一个数与该数的大小关系
        for(int j = 0;j < i;j++){
        	// 如果当前数大于前面的数，则在前面的长度基础上+1，取dp[i]，dp[j] + 1的最大值
            if(nums[i] > nums[j]){
                dp[i] = Math.max(dp[j] + 1,dp[i]);
            }
        }
        // 保存最大长度
        max = Math.max(dp[i],max);
    }
    return max;
}

315. 计算右侧小于当前元素的个数

给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例：

输入：nums = [5,2,6,1]
输出：[2,1,1,0] 
解释：
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素

解题思路：归并排序，在归并的时候，将所有右侧小于当前值的数量统计出来，为了确定下标，归并排序的时候，使用索引数组，对索引数组进行排序，这样就能知道索引下标的位置。
归并排序可以做到部分有序，在部分有序的情况下，可以统计出比当前值小的右侧元素的数量。
例如：

nums = [5,2,6,1]
L:[5] R:[2] 					L:[6] R:[1]								      
统计出5的右侧比5小的数量为1。		统计出6的右侧比6小的数量为1		
L:[2,5] R:[1,6]
统计出2的右侧比2小的数量为1。5的右侧比当前值小的数量为1。

归并完成
[1,2,5,6]
将在归并过程中所有的统计结果累加得到：5的右侧小的数量为2。6右侧小的数量为1。2右侧小的数量为1。
最终结果
[2,1,1,0]

public List<Integer> countSmaller(int[] nums) {
    List<Integer> result = new ArrayList<>();
    int len = nums.length;
    int[] temp = new int[len];
    int[] res = new int[len];
    // 索引数组
    int[] indexes = new int[len];
    for (int i = 0; i < len; i++) {
        indexes[i] = i;
    }
    // temp记录归并排序的中间结果，res记录结果
    mergeAndCountSmaller(nums, 0, len - 1, indexes, temp, res);
    // 把 int[] 转换成为 List<Integer>
    for (int i = 0; i < len; i++) {
        result.add(res[i]);
    }
    return result;
}
//数组 nums 指定的区间 [left, right] 进行归并排序，在排序的过程进行统计
private void mergeAndCountSmaller(int[] nums, int leftStart, int rightEnd, int[] indexes, int[] temp, int[] res) {     
    if(leftStart < rightEnd){
        int mid = leftStart + (rightEnd - leftStart) / 2;
        mergeAndCountSmaller(nums, leftStart, mid, indexes, temp, res);
        mergeAndCountSmaller(nums, mid + 1, rightEnd, indexes, temp, res);
        // 如果索引数组有序，则不存在逆序关系，没有必要合并
        if (nums[indexes[mid]] <= nums[indexes[mid + 1]]) {
            return;
        }
        // 合并两个有序数组
        mergeOfTwoSortedArrAndCountSmaller(nums, leftStart, mid, rightEnd, indexes, temp, res);
    }
}
//[left, mid] 是排好序的，[mid + 1, right] 是排好序的
private void mergeOfTwoSortedArrAndCountSmaller(int[] nums, int leftStart, int mid, int rightEnd, int[] indexes, int[] temp, int[] res) {
    // tmp 辅助数组，记录中间的排序结果
    for (int i = leftStart; i <= rightEnd; i++) {
        temp[i] = indexes[i];
    }
    int rightStart = mid + 1;
    int leftEnd = mid;
    int k = leftStart;
    // 从 leftStart-leftEnd, rightStart-rightEnd 两个区间合并，同时统计右侧的小于的数量。
    while(leftStart <= leftEnd && rightStart <=rightEnd){
        if(nums[temp[leftStart]] <= nums[temp[rightStart]]){
            indexes[k] = temp[leftStart];
            // 统计比 nums[temp[leftStart]] 的值 右侧小的数量。
            res[indexes[k]] += rightStart - mid - 1;
            leftStart++;
        }else{
            indexes[k] = temp[rightStart];
            rightStart++;
        }
        k++;
    }
    while(leftStart <= leftEnd){
        // 此时 [rightStart,rightEnd]区间为空。
        indexes[k] = temp[leftStart];
        // 每一个 nums[indexes[k]] 都比 (mid,rightEnd] 区间的数大。
        res[indexes[k]] += (rightEnd - mid);
        leftStart++;
        k++;
    }
    while(rightStart <= rightEnd){
        // 此时 [leftStart,leftEnd]区间为空。
        indexes[k] = temp[rightStart];
        rightStart++;
        k++;
    }
}

322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。
示例：

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

解题思路：动态规划，dp[i] 表示 钱的总数为 i 时，最少兑换硬币数。
状态转移方程： dp[ i ] = Min(dp[i] , dp[ i - coins[m]]) 。coins[ m ] 为 所有的硬币面额。
初始边界，dp[0] = 0，钱的总数为0时，最少需要0个硬币。

// 动态规划
public int coinChange(int[] coins, int amount) {
    // dp[i] 表示钱的总数为i时，最少兑换硬币数。
    int[] dp = new int[amount + 1];
    // 边界条件
    dp[0] = 0;
    for(int i = 1;i <= amount;i++){
    	// 初始化一个不可能的数
        dp[i] = amount + 1;
        for(int ci = 0;ci < coins.length; ci++){
        	// 防止数组越界
            if(i-coins[ci] >= 0) {
            	// 转移方程
                dp[i] = Math.min(dp[i], dp[i - coins[ci]] + 1);
            }
        }
    }
    // 判断是否能兑换，不能兑换，赋值为 -1
    if(dp[amount] == amount + 1){
        dp[amount] = -1; 
    }
    return dp[amount];
}

324. 摆动排序 II

给你一个整数数组 nums，将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。
你可以假设所有输入数组都可以得到满足题目要求的结果。

示例 ：

输入：nums = [1,5,1,1,6,4]
输出：[1,6,1,5,1,4]
解释：[1,4,1,5,1,6] 同样是符合题目要求的结果，可以被判题程序接受。

提示：

• 1 <= nums.length <= 5 * 104
• 0 <= nums[i] <= 5000
• 题目数据保证，对于给定的输入 nums ，总能产生满足题目要求的结果

方法一：对数组进行排序后，进行逆序穿插排列。
例如：
1，1，2，2，3，3
进行穿插排列后为：
2，3，1，3，1，2

public void wiggleSort(int[] nums) {
    Arrays.sort(nums);
    int[] copy= Arrays.copyOf(nums,nums.length);
    // 1,1,2,2,3,3
    int n = nums.length - 1;
    for (int i = 1; i < nums.length; i += 2) {
        nums[i] = copy[n--];	// x,3,x,3,x,2 
    }
    for (int i = 0; i < nums.length; i += 2) {
        nums[i] = copy[n--];	// 2,3,1,3,1,2
    }
}

方法二：快速选择出数组的中位数，以中位数对数组进行三部划分。小于中位数的，中位数，大于中位数的。然后在进行逆序穿插排列。

void swap(int[] nums,int i,int j){
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}
public void wiggleSort(int[] nums) {
    int len = nums.length;
    int midPtr = nums.length / 2;
    // 找到中位数
    quickSelect(nums, 0, len - 1, midPtr);
    // 将数组进行划分，[小于midPtr,midPtr,大于midPtr]
    int i = 0, j = 0, k = nums.length - 1;
    while(j < k){
    	// 将大于中位数的都往后放
        if(nums[j] > nums[midPtr]){
            swap(nums,k, j);
            --k;
        }else if(nums[j] < nums[midPtr]){
        	// 小于中位数的都往前放
            swap(nums,j,i);
            ++i;
            ++j;
        }
        else{
        	// 中间的自然都是中位数了
            ++j;
        }
    }
    // 进行逆序穿插排列
    int[] copy= Arrays.copyOf(nums,nums.length);
    int n = len - 1;
    for (i = 1; i < nums.length; i += 2) {
        nums[i] = copy[n--];
    }
    for (i = 0; i < nums.length; i += 2) {
        nums[i] = copy[n--];
    }
}
void quickSelect(int[] nums, int start, int end, int midPtr){
    int i = start - 1;
    int j = end;
    // 在[start,end]区间中 随机选择一个枢纽元
    int m = (int)(Math.random() * (end - start) + start);
    // 将枢纽元放在最后
    swap(nums,end,m);
    m = end;
    while(i < j){
        while(i < j && nums[++i] < nums[m]);
        while(i < j && nums[--j] > nums[m]);
        if(i < j){
            swap(nums,i,j);
        }
    }
    // 找到枢纽元正确的位置，放回去
    swap(nums,i,end);
    // 找到中位数
    if(i == midPtr){
        return;
    } else if(i > midPtr){
    	// 当前位置比中位数大
        quickSelect(nums,start,i - 1,midPtr);
    } else {
    	// 当前位置比中位数小
        quickSelect(nums,i + 1,end,midPtr);
    }
}